PTA-二叉搜索树的插入排序

二叉搜索树的插入排序

二叉搜索树定义为：

左子树仅包含小于根结点的元素；
右子树仅包含大于根结点的元素；
左右子树均为二叉搜索树。
一棵二叉搜索树可以有不同的插入顺序。例如，对于如下的二叉搜索树

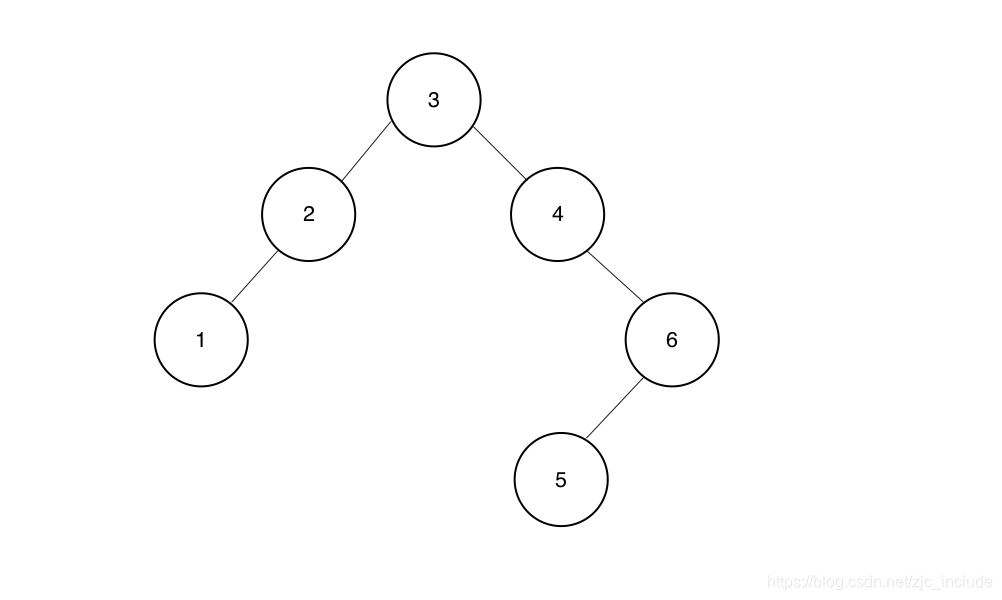
figure.png

插入序列可以是 3 2 1 4 6 5， 也可以是 3 2 4 1 6 5 但不可以是 3 2 4 5 6 1。

下面给出一棵二叉搜索树的先序遍历序列，请编写程序求出该树的插入序列个数。考虑到总数可能非常大，请输出总数对 1000000007 (10
​9
​​ +7)取余的结果。

输入格式:
第一行给出一个整数 N (0<N<=100)，表示二叉树中元素个数；

第二行给出 N 个正整数，以空格分隔，表示二叉树的先序遍历序列；

输出格式:
在一行中输出插入序列总数。

输入样例:
6
3 2 1 4 6 5

输出样例:
10

解题思路

1、先构造杨辉三角（用于存放组合数）。
2、先根据输入的序列先序构造成一个树。
3、根据这个已经构造好的二叉树计算它的插入序列总数，具体计算方式如下
对于一个结点
1、如果是叶子结点，那么它的插入序列只有一种
2、若果只有左子树，那么它的插入序列数和他的左子树一样
3、如果只有右子树，那么它的插入序列数和他的右子树一样
4、如果左右子树都有，则它的插入序列数等于左子树的序列个数右子树的序列个数
(组合数)C（左子树的元素个数+右子树的元素个数）(左子树元素个数)

代码

#include<stdio.h>
#include<stdlib.h>
#include<string.h>
typedef struct node{
   
    //结点结构
    int data; //结点数据
    long n; //当前结点作为根结点时的序列种类
    int num; //当前结点的子树元素的个数
    struct node * lchild; //左孩子
    struct node * rchild; //右孩子
}node,* tree;
tree creattree(int *p,int n){
   
    //先序构建二叉树，P为输入序列首地址，n为元素个数
    tree t; //声明一个结点空间
    if(n<=0||p[0]==-1) //n=0或到达-1则标志已经结束
        return NULL;
    t=(tree)malloc(sizeof(node)); //分配空间
    t->data=p[0]; //当前结点的数据域赋值
    t->n=1; //当前只有一种
    t->num=n; //当前字树元素个数
    int flag; //设立一个标志，用于记录大于根结点的下一个结点的上一个元素的下标
    for