滑动窗口——长度最小的子数组

一.题目描述

LCR 008. 长度最小的子数组 - 力扣（LeetCode）

二.题目解析 

题目还是很好理解的，我们只需要找到一段连续的子数组，让其的和大于等于target即可，但要求是要找到最短的子数组。需要注意，这里的子数组一定得是连续的，比如示例一：[2，3，2]，虽然满足>target，但其并不是连续的子数组。

如果没有满足要求的子数组，返回0即可。

三.算法原理

1.暴力解法

我们可以枚举出所有的子数组，然后遍历子数组求出数组的和sum，判断sum是否满足>=target，在这个过程中更新满足要求的最短长度即可。

时间复杂度：首先我们枚举出所有的子数组需要O(N^2)，然后在遍历每一个子数组，求出sum，这个是O(N)，所以整体的时间复杂度为O(N^3)。

2.对暴力枚举进行优化

暴力枚举是在求出每一个子区间后，在遍历子区间求出sum，所以导致时间复杂度比较高。我们可以在求子区间的同时进行求和。

这样暴力枚举的时间复杂度就可以提升到O(N^2)。

3.利用加法的单调性+滑动窗口(同向双指针) 

3.1单调性

这里的单调性不同于之前数组排序之后的单调性，而是基于数组的元素都是正整数而得出来的单调性。因为数组元素都是正整数，所以每加多加一个数，总和sum就一定会变大。

3.2利用滑动窗口

我们同样使用两个指针来遍历数组，此时两个指针围成的区间就是一段连续的子区间，我们在遍历的同时求出区间的和sum

首先要做到的就是找到满足要求的子区间：sum>=target。所以我们就要让right++，使区间变大。此时sum也一定在变大，直到我们找到sum第一次大于等于target的位置停止。

当满足要求后，我们就求出此时子区间的长度。然后我们right还有必要往右走了么？

答案是没有必要的！因为继续往右走，sum一定比target大，但是len也在变大，而我们要求的是最短的子区间，所以后面一定不可能是结果。

此时我们让left++，同时sum减去left-1位置的值，判断剩下的区间是否满足要求，如果满足，更新 len。重复这个步骤。当right走到结束位置，说明已经没有子区间了，此时遍历结束。

下面给出，示例一的使用滑动窗口的动图过程：

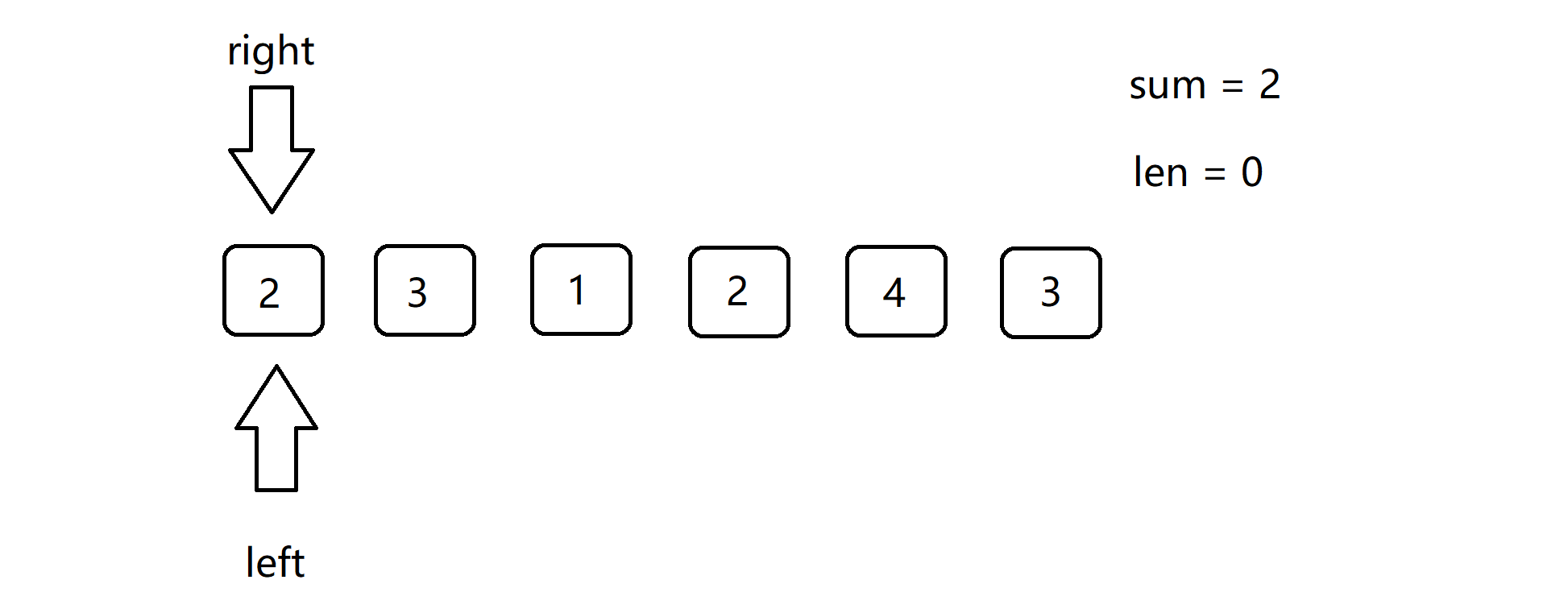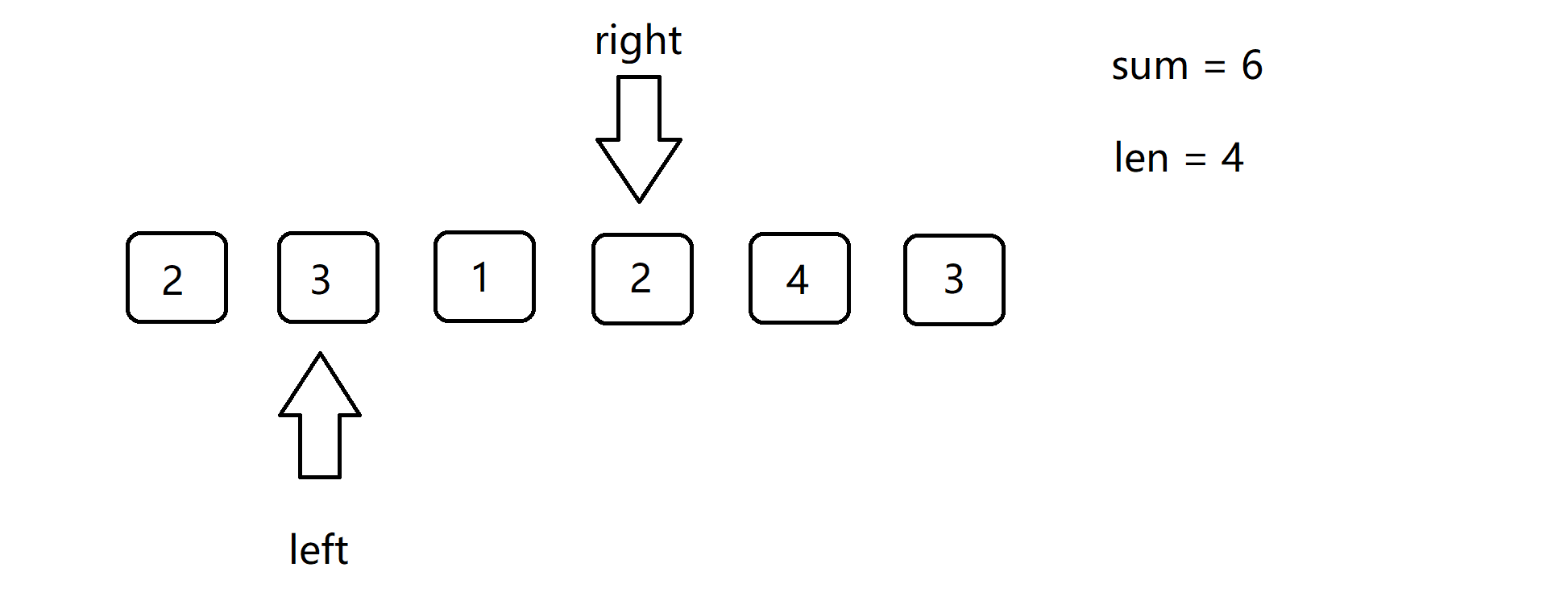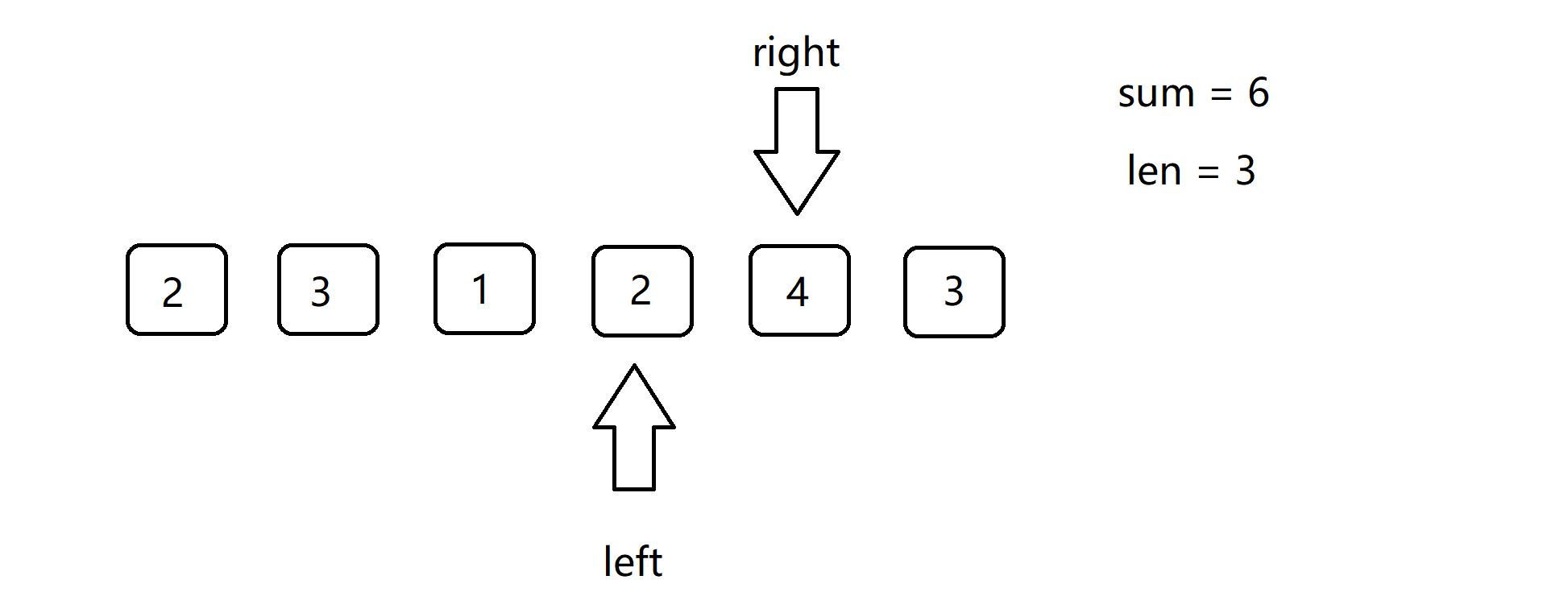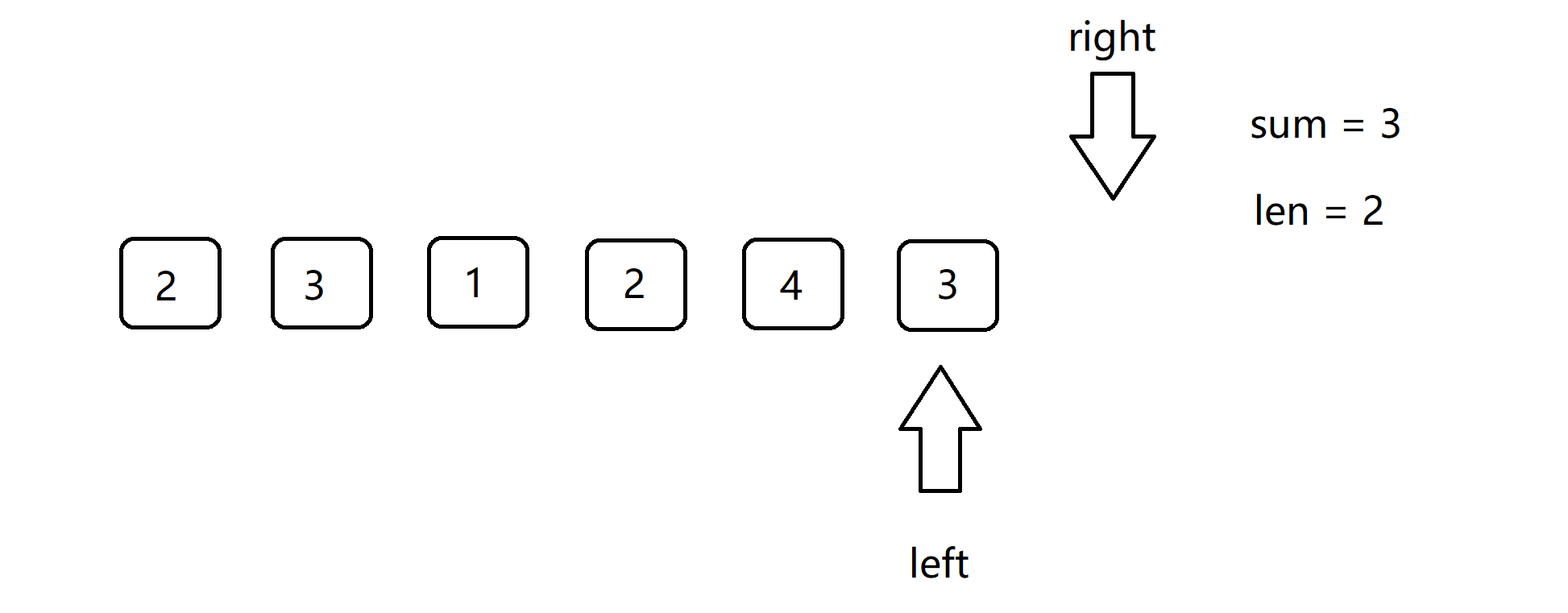
4.滑动窗口的正确性 

很多人刚开始可能有疑问：这个算法好像并没有检查所有的子数组，它的答案一定就是对的么？

没错，就是对的！！！

为什么呢？

这就跟我们的先前提到的单调性有关了。当我们找到满足要求的子区间后，求出len，此时如果继续right++的话，sum还是一定会满足要求，但是len就会变大，所以，当满足要求后，right继续++后的结果一定不是最终答案。

简单来说，就是我们利用正整数相加的单调性规避掉了那些绝对不可能是答案的情况

5.滑动窗口的时间复杂度

我们在选取子区间的时候有一个循环控制right，在这个循环内部如果满足情况也要进行循环进行left++操作，所以是两层循环。但是这里的时间复杂度并不能只看循环的层数来判断。

其实right肯定会遍历一边数组，但是left最好的情况就是不动，最坏的情况就是也遍历到了最后一个位置。

所以综上所述：滑动窗口的时间复杂度为O(2N)~O(N)。

四.代码实现

需要注意这里len的求法，因为len刚开始为0，如果直接求min(len,right-left)的话，那么结果一定是0.所以我们要进行额外判断，避免len一直为0.

int left = 0;
int right = 0;
int sum = 0;
int len = 0;
while (right < nums.size())
{
    sum += nums[right];
    while (sum >= target)
    {
        len = len == 0 ? (right - left + 1) : min(len, right - left + 1);
        left++;
        sum -= nums[left - 1];
    }
    right++;
}
return len;