一.二叉搜索树的概念
二叉搜索树/搜索二叉树,也叫做二叉排序树,它或是一颗空树,或是具有以下性质的二叉树:
1、若它的左子树不为空,那它左子树上的所有节点的值都小于等于根节点的值;
2、若它的右子树不为空,那它右子树上的所有节点的值都大于等于根节点的值;
3、它的左右子树也是二叉搜索树;
4、二叉搜索树既可以插入相同的值,也可以不插入相同的值,具体看场景,map/set/multimap/multiset的底层就是二叉搜索树,其中map/set不支持插入相同的值,multimap/multiset支持插入相同的值。
二.二叉搜索树的性能分析
对于二叉搜索树的插入和删除来说,我们都要先要进行查找。所以遍历二叉搜索树的效率就非常重要了。
对于最好的情况来说,二叉搜索树是一个完全二叉树(近似于完全二叉树),假设有N的节点,那么它的高度为log(N),所以遍历这棵树的时间复杂度为O(log(N));
对于最坏情况来说,二叉搜索树类似于一颗单边树,它的节点全部都在树的一侧分布,此时它的结构就类似于链表的结构了,假设有N个节点,那么它的高度就是N,所以遍历这个树的时间复杂度为O(N).
所以综合来看,查找二叉搜索树节点的时间复杂度为O(N)。
三.二叉搜索树的结构
二叉搜索树是由一个一个节点组成的,所以我们首先要有一个节点类,类中包含了节点存储的数据_key,以及指向左孩子和右孩子的指针。
二叉搜索树这个类我们可以只使用一个根节点的指针来维护。
//二叉搜索树节点
template <typename K>
struct bstreeNode
{
K _key;
bstreeNode<K>* _left;
bstreeNode<K>* right;
bstreeNode(const K& key)
:_key(k)
,_left(nullptr)
,_right(nullptr)
{}
};
//二叉搜索树
template <typename K>
class bstree
{
typedef bstreeNode<K> node
private:
node* _root = nullptr;
};四.插入
1、树为空,直接新增节点,让root指向这个新增节点即可。
2、树不为空,以此与节点进行比较,如果插入值大于该结点的值就向右走,如果插入值小于该节点的值就像左走,直到走到空时,插入到这个位置。
3、含重复值,与第二点逻辑类似,只不过遇到相等的值是规定一个统一的移动方向,不要一会左一会右。
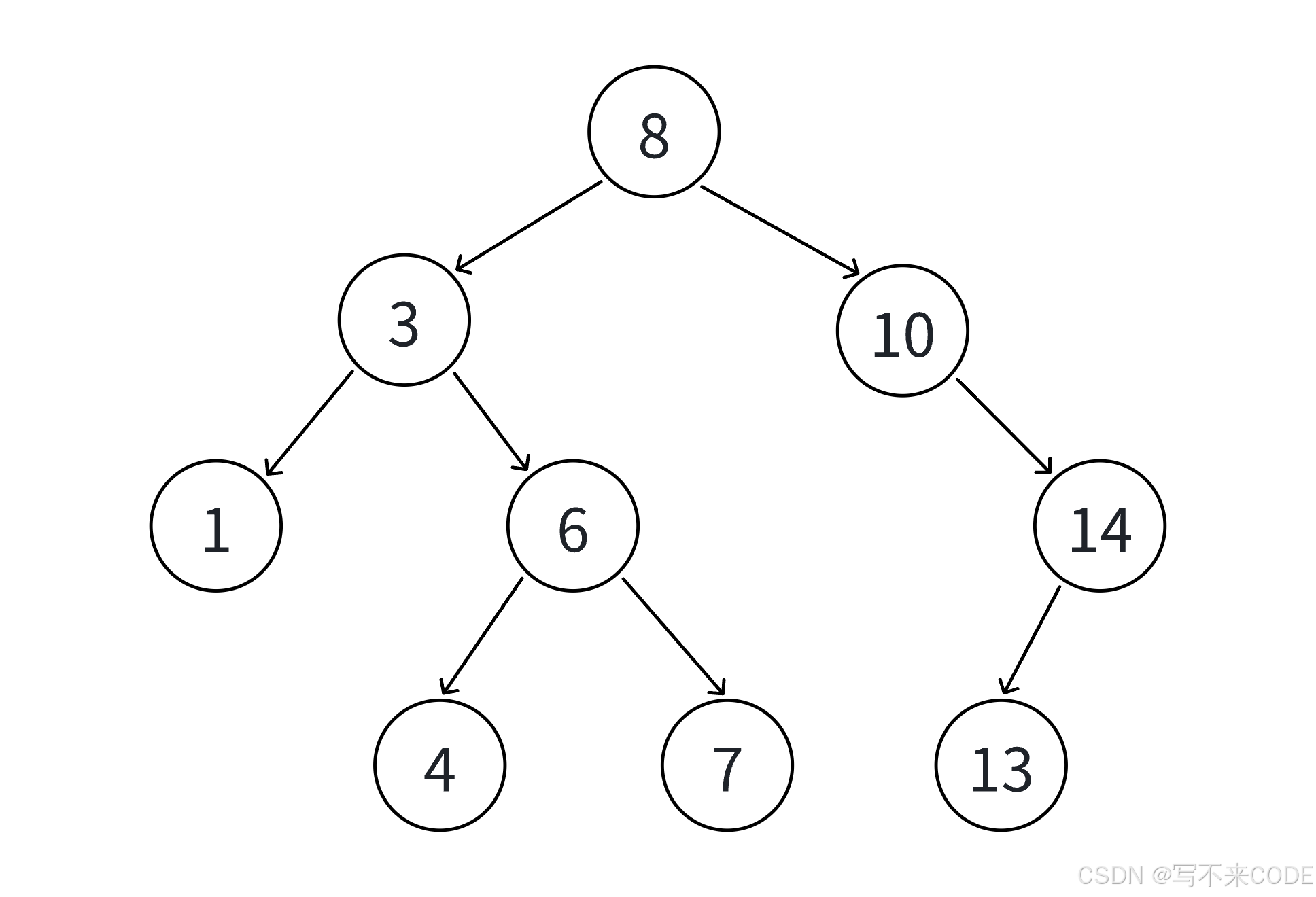
我们需要用一个cur变量来遍历二叉搜索树,用它找到位置后,我们要想把它链到树上的话,还需要这个位置的父亲节点,所以我们还要创建一个父亲节点,用来记录cur的父节点。
链接的时候不可以直接连接,因为我们不知道把新节点连接到parent的左边还是右边,所以我们先要进行判断,然后再进行连接。
bool Insert(const K& key)
{
//树为空
if (_root == nullptr)
{
_root = new node(key);
return true;
}
else//树不为空
{
node* cur = _root;
node* parent = nullptr;
while (cur)
{
if (key > cur->_key)
{
parent = cur;
cur = cur->_right;
}
else if (key < cur->_key)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
//创建新节点,判断cur位于parent的那边
node* newnode = new node(key);
if (parent->_key > newnode->_key)
{
parent->_left = newnode;
}
else
{
parent->_right = newnode;
}
return true;
}
}五.中序遍历二叉搜索树
我们仔细观察这个二叉树的构造,如果采取中序遍历的话,结果就是有序的。
中序遍历的规则是 左子树-根-右子树
void _Inorder(const node* root)
{
if (root == nullptr)
{
return;
}
_Inorder(root->_left);
cout << root->_key << " ";
_Inorder(root->_right);
}如果我们将中序遍历定义为公有的话,我们有两种方法:
1、不传参数,直接使用this指针,但是这种方式的话,我们无法使用递归来遍历二叉树:首先,我们不可以传参数,其次, 我们无法调用该函数,因为该函数是二叉树的行为,而不是节点的行为,_root->left是一个节点,无法调用该函数
void _Inorder() { if (_root == nullptr) { return; } _root->left->_Inorder(); cout << _root->_key << " "; _root->_right->_Inorder(); }2、传参数,但是要穿根节点,而根节点是私有成员变量,如果公开的话,会破坏类的封装性。
所以将该函数公有是不合理的,所以我们选择将其私有,但是私有的话,也要传参数,并且类外无法访问,那要如何实现呢?
我们可以定义一个外壳程序,将他公有,他可以调用该遍历函数,而且也可以使用root,直接传给该函数即可。
public:
void Inorder()
{
_Inorder(_root);
}
private:
void _Inorder(const node* root)
{
if (root == nullptr)
{
return;
}
_Inorder(root->_left);
cout << root->_key << " ";
_Inorder(root->_right);
}六.查找
查找的逻辑与插入的逻辑类似,也是一个一个的比较,大于根节点就向右走,小于就向左走,等于就找到了,如果走到了空,就说明这棵树中没有该节点,返回false即可。
bool find(const K& key)
{
node* cur = _root;
while (cur)
{
if (key > cur->_key)
{
cur = cur->_right;
}
else if (key < cur->_key)
{
cur = cur->_left;
}
else
{
return true;
}
}
return false;
}七.删除
删除指定元素,首先我们要先查找该元素是否存在,如果不存在直接返回false。
bool Erase(const K& key)
{
node* cur = _root;
while (cur)
{
if (key > cur->_key)
{
cur = cur->_right;
}
else if (key < cur->_key)
{
cur = cur->_left;
}
else
{
//删除操作
return true;
}
}
return false;
}1、如果删除的是叶子节点的话,直接删除该节点,然后让指向该节点的指针指向空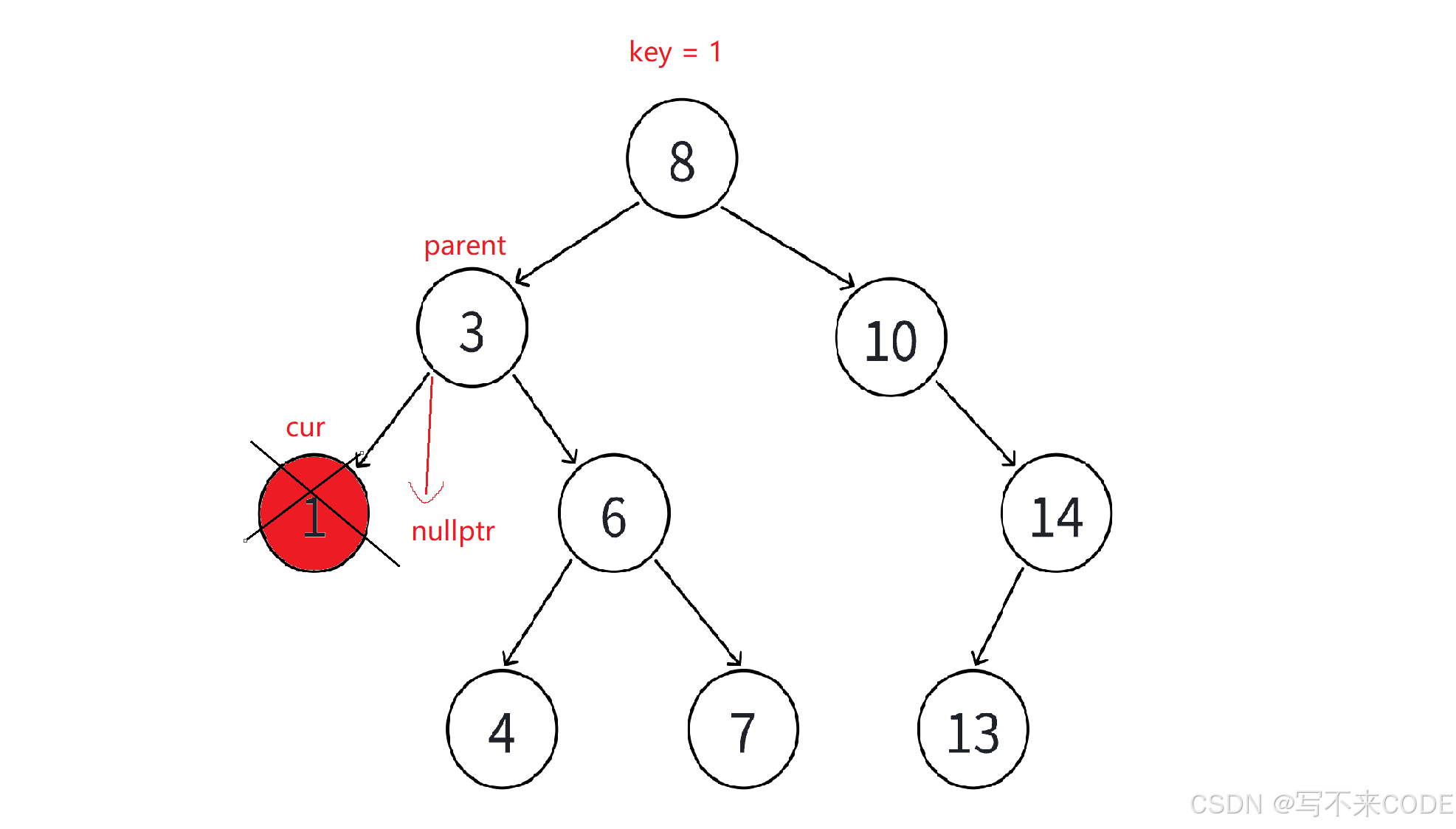
2、如果删除的节点N左孩子为空,那么就让父亲节点的对应指针指向N节点的右孩子,然后删除N节点
3、如果删除的节点N右孩子为空,那么就让父亲节点的对应指针指向N节点的左孩子,然后删除N节点
上面三种情况比较简单,而且第一种情况可以归到第二种/第三种,所以我们没有必要自己专门写一个针对叶子结点的删除
需要注意的是,当上面这三种情况遇到删除的是根节点时,需要特殊处理,直接将不为空的那一支赋值给_root,然后删除cur即可

4、如果删除的节点N左右孩子都不为空,有两种删除方式:
- 找到节点N的左子树的最右节点,因为删除之后要保证依旧是二叉搜索树,而N节点的左子树中都是比N小的值,而其中最右节点是左子树中最大的,然后将该处的值赋值给N节点,这样,就可以满足N节点的值比左子树的值大,比右子树的值小,然后删除该节点即可。
- 找到节点N的右子树的最左节点,这个节点比N大,但又是右子树中最小的,所以交换之后依旧可以保证该树依旧是二叉搜索树。
这里以找左子树的最右节点来分析:
我们要删除8,所以我们先创建replace用来寻找要替代的元素,因为是左子树的最右节点,所以replace的初始值就是cur->_left,replaceParent = cur。然后replace一直向右走,直到走到空,期间replaceParent也要跟着变化,找到后将replace的值赋给cur,然后删除repalce。
删除replace时,虽然其右子树为空,但是左子树不一定为空,所以我们不管是否为空,都直接将repalceParent的对应指针指向repalce的左孩子。如果不为空,刚好可以连接上,如果为空,replaceParent刚好指向空。

bool Erase(const K& key)
{
node* parent = nullptr;
node* cur = _root;
while (cur)
{
if (key > cur->_key)
{
parent = cur;
cur = cur->_right;
}
else if (key < cur->_key)
{
parent = cur;
cur = cur->_left;
}
else
{
//找到了指定数据
//此时cur指向的就是待删除的数据,parent就是待删除节点的父亲节点
if (cur->_left == nullptr)// 左孩子为空 , 叶子节点
{
if (cur == _root)
{
_root = cur->_right;
}
else
{
if (parent->_left == cur)
{
parent->_left = cur->_right;
}
else
{
parent->_right = cur->_right;
}
delete cur;
cur = nullptr;
}
}
else if (cur->_right == nullptr)//右孩子为空
{
if (cur == _root)
{
_root = cur->_left;
}
else
{
if (parent->_left == cur)
{
parent->_left = cur->_left;
}
else
{
parent->_right = cur->_left;
}
delete cur;
cur = nullptr;
}
}
else//左右孩子都不为空
{
//找左子树的最右节点
node* replace = cur->_left;//最右节点
node* replaceParent = cur;//最右节点的父亲
while (replace->_right)
{
replaceParent = replace;
replace = replace->_right;
}
cur->_key = replace->_key;//覆盖要删除的数
//删除replace
//不论replace是否有左孩子,都直接与replaceParent连接
if (replaceParent->_left == replace)
{
replaceParent->_left = replace->_left;
}
else
{
replaceParent->_right = replace->_left;
}
delete replace;
replace = nullptr;
}
return true;
}
}
return false;
}八.二叉搜索树的key和key/value使用场景
1.key搜索场景
在二叉树搜索树的节点中,只有key作为关键码,节点中只需要存储key即可。关键码即为需要搜素的值,搜索场景只需要判断key在没在。key的搜索场景实现的二叉搜索树支持增删查,但是不支持修改,修改会破坏搜索树的结构,使其不满足二叉搜索树的性质。
场景1:
小区的无人值守车库,买了小区车位的业主的车才能进入小区,物业会将业主的车牌录入到后台系统,车辆进入时扫描车牌在不在系统中,在的话就抬杆,不在就不抬杆。
场景2:
检查一篇英文文章中的单词是否拼写正确,将所有的单词都放入一个二叉搜索树中,读取文章的单词,在二叉树中进行查找,如果没有的话就标红

2.key/value搜索场景
每一个关键码key,都有一个与之对应的value,value可以是任意类型的对象。二叉树的节点除了要存储key还需要存储对应的value。
增删查还是利用key的逻辑,因为查找时只根据关键码进行查找,这样可以快速找到key对应的value。
key/value支持二叉搜索树的修改,但是不是修改key,而是key对应的value。
场景一:
简单的中英文互译字典,树的节点存储key(英文)和vlaue(中文),搜索时输入英文,找到该英文时,就找到了对应的中文。
场景二:
商场的无人值守车库,入场时扫描车牌,记录车牌以及进入的时间,出车库时,扫描车牌,在后台中去搜索该车牌,找到对应的入场时间,用现在的时间-入场时间得出停车时长,然后计算出停车费,缴费后抬杆离场。
场景三:
统计一篇文章中单词的出现次数,读取一个单词,查找单词是否存在,若不存在则说明这个单词第一个出现,count = 1,单词存在,count++.
3.key/value二叉树的实现
key/value的实现只需要在key的基础上进行修改即可:
节点增加一个模板参数,用来存储value
插入时不仅要插入key还要插入value
删除时当删除的节点左右孩子都在时,需要替换,替换时要将value和key都替换
find函数返回值不再是bool,而应该是指定key的节点指针,如果没有则返回nullptr。
namespace key_value
{
//二叉搜索树节点
template <typename K, typename T>
struct bstreeNode
{
K _key;
T _value;
bstreeNode<K, T>* _left;
bstreeNode<K, T>* _right;
bstreeNode(const K& key,const T& value)
:_key(key)
, _value(value)
, _left(nullptr)
, _right(nullptr)
{}
};
//二叉搜索树
template <typename K, typename T>
class bstree
{
typedef bstreeNode<K,T> node;
public:
bool Insert(const K& key,const T& value)
{
//树为空
if (_root == nullptr)
{
_root = new node(key,value);
return true;
}
else//树不为空
{
node* cur = _root;
node* parent = nullptr;
while (cur)
{
if (key > cur->_key)
{
parent = cur;
cur = cur->_right;
}
else if (key < cur->_key)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
//创建新节点,判断cur位于parent的那边
node* newnode = new node(key,value);
if (parent->_key > newnode->_key)
{
parent->_left = newnode;
}
else
{
parent->_right = newnode;
}
return true;
}
}
node* find(const K& key)
{
node* cur = _root;
while (cur)
{
if (key > cur->_key)
{
cur = cur->_right;
}
else if (key < cur->_key)
{
cur = cur->_left;
}
else
{
return cur;
}
}
return nullptr;
}
void Inorder()
{
_Inorder(_root);
cout << endl;
}
bool Erase(const K& key)
{
node* parent = nullptr;
node* cur = _root;
while (cur)
{
if (key > cur->_key)
{
parent = cur;
cur = cur->_right;
}
else if (key < cur->_key)
{
parent = cur;
cur = cur->_left;
}
else
{
//找到了指定数据
//此时cur指向的就是待删除的数据,parent就是待删除节点的父亲节点
if (cur->_left == nullptr)// 左孩子为空 , 叶子节点
{
if (cur == _root)
{
_root = cur->_right;
}
else
{
if (parent->_left == cur)
{
parent->_left = cur->_right;
}
else
{
parent->_right = cur->_right;
}
delete cur;
cur = nullptr;
}
}
else if (cur->_right == nullptr)//右孩子为空
{
if (cur == _root)
{
_root = cur->_left;
}
else
{
if (parent->_left == cur)
{
parent->_left = cur->_left;
}
else
{
parent->_right = cur->_left;
}
delete cur;
cur = nullptr;
}
}
else//左右孩子都不为空
{
//找左子树的最右节点
node* replace = cur->_left;//最右节点
node* replaceParent = cur;//最右节点的父亲
while (replace->_right)
{
replaceParent = replace;
replace = replace->_right;
}
//覆盖要删除的数
cur->_key = replace->_key;
cur->_value = replace->_value;
//删除replace
//不论replace是否有左孩子,都直接与replaceParent连接
if (replaceParent->_left == replace)
{
replaceParent->_left = replace->_left;
}
else
{
replaceParent->_right = replace->_left;
}
delete replace;
replace = nullptr;
}
return true;
}
}
return false;
}
private:
void _Inorder(const node* root)
{
if (root == nullptr)
{
return;
}
_Inorder(root->_left);
cout << root->_key << ":" << root->_value << endl;
_Inorder(root->_right);
}
node* _root = nullptr;
};
}3.1key/value的析构
我们在删除树的节点时要递归着删除,根据后序遍历的顺序进行删除,这里遇到的问题与中序遍历打印该树的节点是一致的,所以我们也采取一个外壳程序来调用真正的销毁。
public:
~bstree()
{
Destroy(_root);
}
private:
void Destroy(const node* root)
{
if (root == nullptr)
{
return;
}
Destroy(root->_left);
Destroy(root->_right);
delete root;
root = nullptr;
}3.2key/value的拷贝构造
默认生成的拷贝构造会进行浅拷贝,浅拷贝在析构时就会出现问题,对同一块空间进行了多次的释放,所以我们要显示的实现拷贝构造。
拷贝构造依旧得借助递归来实现,要根据前序遍历的顺序将节点一个一个的复制出来.
需要注意的是,当我们实现了拷贝构造后,编译器就不会再自己生成默认构造了,所以我们要强制生成一个默认构造:
bstree() = default;//C++11强制生成默认构造
public:
bstree() = default;
bstree(const bstree& t)
{
_root = Copy(t._root);
}
private:
node* Copy(const node* root)
{
if (root == nullptr)
{
return nullptr;
}
node* newroot = new node(root->_key, root->_value);
newroot->_left = Copy(root->_left);
newroot->_right = Copy(root->_right);
return newroot;
}3.3key/value的赋值运算符重载
赋值运算符重载我们使用现代写法即可,因为这是交换的是指针,所以我们不必要自己写一个交换函数来避免深拷贝。
bstree& operator=(bstree t)
{
std::swap(_root,t._root);
return *this;
}完!
























 2153
2153

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








