曼哈顿距离

两点间的曼哈顿距离d = | x1 - x2 | + | y1 - y2 |

两点间的欧氏距离d = sqrt( (x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2) )

其中打印菱形可以用曼哈顿距离很好的解决

代码如下：

#include <bits/stdc++.h>
using namespace std;
int main(){
    int n;
    cin >> n;
    int x = n / 2, y = n / 2;
    for(int i = 0; i < n; i++){
        for(int j = 0; j < n; j++){
            if(abs(i - x) + abs(j - y) <= n / 2)cout << "*";
            else cout << " ";
        }
        cout << endl;
    }
    return 0;
}

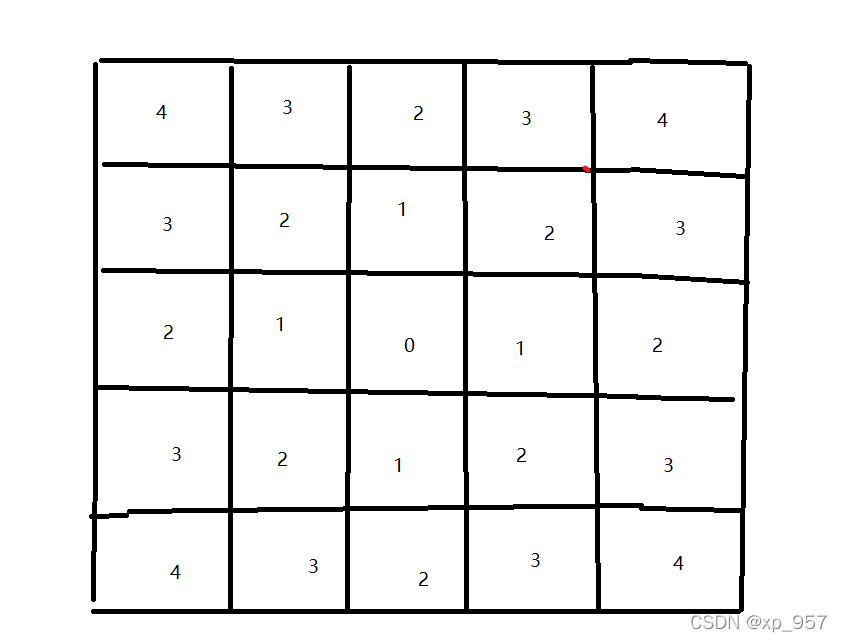
 数字代表距离中心点的距离，要打印五阶菱形，只需曼哈顿距离小于5/2即可。

要想打印出n阶菱形，只需要将与原点距离的曼哈顿距离为小于等于 n/2(向下取整)。