二叉树的创建与遍历

最新推荐文章于 2024-05-29 09:00:00 发布

原创最新推荐文章于 2024-05-29 09:00:00 发布 · 373 阅读

4 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #数据结构 #c++

1、递归创建

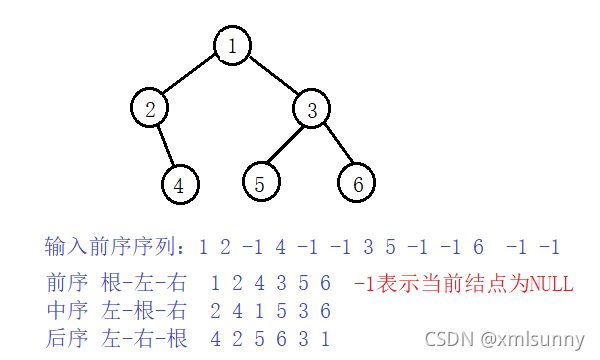
根据前序序列创建二叉树，当所有节点的左右孩子为NULL，则停止创建

#include<iostream>
using namespace std;
#include<vector>
#include<algorithm>
#include<stack>
#include<queue>

//树结点
struct TreeNode
{
	int val;
	TreeNode* left;
	TreeNode* right;

	TreeNode(int x) :val(x), left(NULL), right(NULL)
	{
	}
};

//1、递归创建 
TreeNode* createBTree()
{
	TreeNode* root = new TreeNode(0);
	int val;
	cin >> val;

	if (val == -1)
		root = NULL;
	else
	{
		root->val = val;
		root->left = createBTree(); //递归创建
		root->right = createBTree();
	}
	return root;
}

2、递归遍历(深度优先)

前序：根-左-右

中序：左-右-根

后序：左-右-根

//2、递归遍历 前序
void preorderTravl(TreeNode* root)
{
	if (root == NULL)
		return;

	cout << root->val << " ";
	preorderTravl(root->left);
	preorderTravl(root->right);
	
	
}
//     中序
void inorderTravl(TreeNode* root)
{
	if (root == NULL)
		return;

		inorderTravl(root->left); //左
		cout << root->val << " "; //根
		inorderTravl(root->right); //右	
}

//     后序
void postorderTravl(TreeNode* root)
{
	if (root == NULL) 
		return;
	
	postorderTravl(root->left);
	postorderTravl(root->right);
	cout << root->val << " ";	
}

int main()
{
    //创建二叉树
	TreeNode* root = createBTree();

    //前序遍历
    preorderTravl(root);
	cout << endl;
    //中序遍历
	inorderTravl(root);
	cout << endl;
    //后序遍历
	postorderTravl(root);
	cout << endl;

	return 0;
}

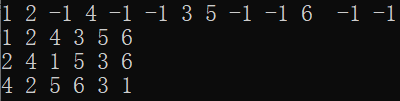
结果如下：

3、迭代遍历(深度优先)

递归遍历时，隐式地维护了一个栈，我们将这个栈显示的写出来

(1)对于前序遍历，根-左-右

栈：先进后出，所以每次根节点root入栈出栈，然后右、左节点依次入栈，则出栈顺序左-右

//3、迭代遍历  前序
void preorderTravl(TreeNode* root)
{
	stack<TreeNode*> s;

	//根节点非空，入栈
	if (root)
		s.push(root); 

	//栈非空 执行 root出栈，然后right、left依次入栈
	while (!s.empty())
	{
		TreeNode* curNode = s.top(); //记录栈顶节点,即root节点
		cout << curNode->val << " ";

		s.pop(); //root出栈	
		
		if (curNode->right) //当前节点右孩子非空，入栈
			s.push(curNode->right); 
		if (curNode->left) //当前节点左孩子非空，入栈
			s.push(curNode->left);
	}
}

(2)对于中序遍历，左-根-右

与前序遍历不同，前序遍历遇到根节点直接输出。而中序遍历需要先找到根节点的左孩子。

我们应该先找到当前节点的最左侧的节点，沿路节点入栈，栈中节点都是某个节点的左孩子。

step1:一直找当前节点的最左侧节点，沿路访问的节点都入栈，栈顶元素为最左侧节点，出栈；

step2:若当前栈顶节点有右孩子，重复step1找右孩子的最左侧节点

重复以上过程，直至栈为空

如图： 1 2 // 入栈

1 // 栈顶2出栈

1 4 // 2有右孩子4,4入栈，找4的左孩子，沿路节点入栈

1 //4出栈，没有右孩子停止

3 5 // 1出栈，1有右孩子，找右孩子最左侧的节点，沿路节点入栈

3 //5出栈，没有右孩子停止

6 // 3出栈，3有右孩子，找右孩子最左侧的节点，沿路节点入栈

//6出栈，没有右孩子停止

出栈顺序：2 4 1 5 3 6 即为中序遍历序列

//3、迭代遍历  中序
void inorderTravl(TreeNode* root)
{
	stack<TreeNode*> s;	

	while (root || !s.empty())
	{
		//找最左侧左孩子，沿路节点入栈
		while (root)
		{
			s.push(root);
			root = root->left;
		}

		TreeNode* curNode = s.top(); //当前栈顶元素为最左侧孩子
		cout << curNode->val << " "; //输出

		s.pop(); //出栈

		if (curNode->right) //当前节点有右孩子
			root = curNode->right; //对右孩子执行以上过程
	}
}

(3)对于后序遍历，左-右-根

与前序类似，根入栈出栈，然后左、右孩子入栈，出栈顺序右-左

得到序列：根 - 右- 左将结果存起来，然后反转得到后序序列：左-右-根

//3、迭代遍历 后序
void postorderTravl(TreeNode* root)
{
	stack<TreeNode*> s;
	vector<int> res;
	//根节点非空，入栈
	if (root)
		s.push(root);

	//栈非空 执行 root出栈，然后left、right依次入栈
	while (!s.empty())
	{
		TreeNode* curNode = s.top(); //记录栈顶节点,即root节点
		//cout << curNode->val << " ";
		res.push_back(curNode->val); //保存结果

		s.pop(); //root出栈	

		
		if (curNode->left) //当前节点左孩子非空，入栈
			s.push(curNode->left);
		if (curNode->right) //当前节点右孩子非空，入栈
			s.push(curNode->right);
	}
	//将结果反转，然后输出  根-右-左  反转   左-右-根
	reverse(res.begin(), res.end());
	for (auto it : res)
		cout << it << " ";
}

迭代遍历结果如下，可见结果与递归遍历相同

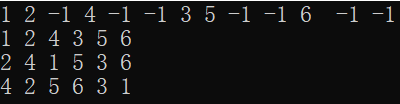
4、层序遍历(宽度优先)

层序，使用队列实现，将每个节点的左右孩子都入队，然后依次出队

先进先出，1 2 3 4 5 6

//层序遍历  宽度优先
void levelOrderTravl(TreeNode* root)
{
	queue<TreeNode*> q;

    //根节点入队
	if (root)
		q.push(root);

	while (!q.empty())
	{
		int curSize = q.size(); //当前队列的大小

		for (int i = 0; i < curSize; i++)
		{
			TreeNode* curNode = q.front();//记录当前队首元素
			cout << curNode->val << " "; //输出结果

			q.pop(); //队首元素出队
            
            //左右孩子都入队
			if (curNode->left)
				q.push(curNode->left);
			if (curNode->right)
				q.push(curNode->right);
		}
	}
}