leetcode笔记--代码随想录--单调栈

1、739. 每日温度

单调栈的思想是存储单调增加/减小的下标，这里存储下标是因为题目一般会用到索引信息。

自己想的有些复杂，想着存储递增的可以在栈中得到索引，但存储递减的话也是能得到的，当前存储的时候的i就是在栈中比它小的那些索引对应的数值。

想问题还是有些太直接了。

class Solution {
    public int[] dailyTemperatures(int[] temperatures) {
        Stack<Integer>  st= new Stack<>();
        int len = temperatures.length;
        int[] res = new int[len];
        st.push(len-1);
        int i= len - 2;
        while(i >= 0){
            if(st.empty()){
                st.push(i);
                i --;
                continue;
            } 
            else if(temperatures[st.peek()] > temperatures[i]){
                res[i] = st.peek() - i ;
                st.push(i);
                i --;
                continue;
            }
            while(!st.empty() &&temperatures[st.peek()] <= temperatures[i]){
                st.pop();
            }            
        }
        return res;

    }
}

2、496.下一个更大元素 I

理解错题意了。。

这个题目不难。

class Solution {
    public int[] nextGreaterElement(int[] nums1, int[] nums2) {
        Stack<Integer> temp = new Stack<>();
        int[] res = new int[nums1.length];
        Arrays.fill(res,-1);
        HashMap<Integer, Integer> hashMap = new HashMap<>();
        for (int i = 0 ; i< nums1.length ; i++){
            hashMap.put(nums1[i],i);
        }
        temp.add(0);
        for (int i = 1; i < nums2.length; i++) {
            if (nums2[i] <= nums2[temp.peek()]) {
                temp.add(i);
            } else {
                while (!temp.isEmpty() && nums2[temp.peek()] < nums2[i]) {
                    if (hashMap.containsKey(nums2[temp.peek()])){
                        Integer index = hashMap.get(nums2[temp.peek()]);
                        res[index] = nums2[i];
                    }
                    temp.pop();
                }
                temp.add(i);
            }
        }

        return res;
    }
}

3、503.下一个更大元素II

这个题比较典型吧，这是加了一个循环，多了一轮的处理。

注意while循环，，这个容易忘记。

class Solution {
    public int[] nextGreaterElements(int[] nums) {
        int[] res = new int[nums.length];
        Stack<Integer> st = new Stack<>();
        st.push(0);
        Arrays.fill(res, -1);
        for(int i=1 ; i< nums.length * 2 ; i++){
            while(!st.empty() && nums[st.peek()] < nums[i % nums.length]){
                res[st.pop()] = nums[i % nums.length];
            }
            st.push(i % nums.length);
            
        }

        return res;

    }
}

4、42. 接雨水

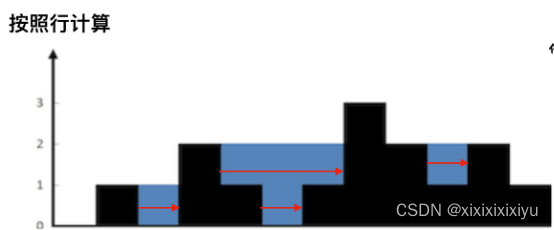
用单调栈的方法需要一行一行算，而不是一列。

列不行的原因是无法通过当前状态就确定这个列的数值应该是多少，也无法通过叠加的方式得到。

掌握这个思路就好写多了。

class Solution {
    public int trap(int[] height){
        int size = height.length;

        if (size <= 2) return 0;

        // in the stack, we push the index of array
        // using height[] to access the real height
        Stack<Integer> stack = new Stack<Integer>();
        stack.push(0);

        int sum = 0;
        for (int index = 1; index < size; index++){
            int stackTop = stack.peek();
            if (height[index] < height[stackTop]){
                stack.push(index);
            }else if (height[index] == height[stackTop]){
                // 因为相等的相邻墙，左边一个是不可能存放雨水的，所以pop左边的index, push当前的index
                stack.pop();
                stack.push(index);
            }else{
                //pop up all lower value
                int heightAtIdx = height[index];
                while (!stack.isEmpty() && (heightAtIdx > height[stackTop])){
                    int mid = stack.pop();

                    if (!stack.isEmpty()){
                        int left = stack.peek();

                        int h = Math.min(height[left], height[index]) - height[mid];
                        int w = index - left - 1;
                        int hold = h * w;
                        if (hold > 0) sum += hold;
                        stackTop = stack.peek();
                    }
                }
                stack.push(index);
            }
        }

        return sum;
    }
}

5、84.柱状图中最大的矩形

算的是局部和，当出现两边低中间高的情况就开始计算。至于为什么这么算，主要在于求面积的高就是当前在栈顶处且当前遍历的元素小于他，并且宽是从栈顶到当前遍历的元素。

另外因为栈是升序，所以会栈顶第二个位置的元素跟栈顶元素之间的元素是大于他们的。

很巧妙。

class Solution {
    int largestRectangleArea(int[] heights) {
        Stack<Integer> st = new Stack<Integer>();
        
        // 数组扩容，在头和尾各加入一个元素
        int [] newHeights = new int[heights.length + 2];
        newHeights[0] = 0;
        newHeights[newHeights.length - 1] = 0;
        for (int index = 0; index < heights.length; index++){
            newHeights[index + 1] = heights[index];
        }

        heights = newHeights;
        
        st.push(0);
        int result = 0;
        // 第一个元素已经入栈，从下标1开始
        for (int i = 1; i < heights.length; i++) {
            // 注意heights[i] 是和heights[st.top()] 比较 ，st.top()是下标
            if (heights[i] > heights[st.peek()]) {
                st.push(i);
            } else if (heights[i] == heights[st.peek()]) {
                st.pop(); // 这个可以加，可以不加，效果一样，思路不同
                st.push(i);
            } else {
                while (heights[i] < heights[st.peek()]) { // 注意是while
                    int mid = st.peek();
                    st.pop();
                    int left = st.peek();
                    int right = i;
                    int w = right - left - 1;
                    int h = heights[mid];
                    result = Math.max(result, w * h);
                }
                st.push(i);
            }
        }
        return result;
    }
}