字典树 (Trie) | 插入和搜索

Trie即字典树是一种高效的信息检索数据结构。使用 Trie，搜索时间复杂性可以达到最佳（Key的长度）。如果我们将Key存储在二叉搜索树中，平衡良好的 BST 的各种操作的时间复杂度与M * log N成正比，其中 M 是最大字符串长度，N 是树中Key的数量。使用 Trie，我们可以在 O(M) 时间内搜索到Key，但是，Trie 的缺点是对存储要求很高即空间复杂度较高。

 

Trie 的每个节点都由多个分支组成。每个分支代表一个可能的键。我们需要将每个键的最后一个节点标记为词节点的结尾。Trie 节点字段isEndOfWord用于将节点区分为词节点的结尾。表示英文字母节点的简单结构如下，

/ Trie node 
struct TrieNode 
{ 
     struct TrieNode *children[ALPHABET_SIZE];
     // 如果节点 
     // 表示单词的结尾， 则 isEndOfWord 为真
     bool isEndOfWord; 
}; 

简单的Trie结构 

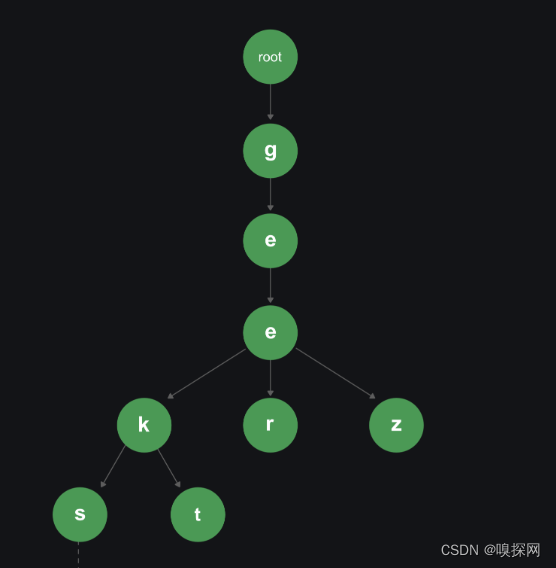
将单词插入 Trie 的方法很简单。单词的每个字母都作为一个单独的 Trie 节点插入。请注意，children即Trie节点的子节点是指向下一级 trie 节点的指针（或引用）数组。单词的字母充当数组children的索引。如果插入的单词是新的或者是现有词的扩展，我们需要构造新的节点。如果新插入的词是Trie中现有词的前缀，我们只需将这个词的最后一个字母标记为该词的结尾。词的长度决定了 Trie 深度。  

搜索操作类似于插入操作，但是我们只比较字符串中的元素并向下移动。由于isEndOfWord为true或 trie 中缺少指向下一层的子节点，则搜索终止。如果最后一个节点的isEndofWord字段为true，则该键存在于 trie 中。在第二种情况下，搜索被迫终于并未完整遍历字符串，因为字符串不存在于 trie 中。

图解

代码实现

class TrieNode:
	
	# Trie node class
	def __init__(self):
		self.children = [None]*26

		# isEndOfWord is True if node represent the end of the word
		self.isEndOfWord = False

class Trie:
	
	# Trie data structure class
	def __init__(self):
		self.root = self.getNode()

	def getNode(self):
	
		# Returns new trie node (initialized to NULLs)
		return TrieNode()

	def _charToIndex(self,ch):
		
		# private helper function
		# Converts key current character into index
		# use only 'a' through 'z' and lower case
		
		return ord(ch)-ord('a')


	def insert(self,key):
		
		# If not present, inserts key into trie
		# If the key is prefix of trie node,
		# just marks leaf node
		pCrawl = self.root
		length = len(key)
		for level in range(length):
			index = self._charToIndex(key[level])

			# if current character is not present
			if not pCrawl.children[index]:
				pCrawl.children[index] = self.getNode()
			pCrawl = pCrawl.children[index]

		# mark last node as leaf
		pCrawl.isEndOfWord = True

	def search(self, key):
		
		# Search key in the trie
		# Returns true if key presents
		# in trie, else false
		pCrawl = self.root
		length = len(key)
		for level in range(length):
			index = self._charToIndex(key[level])
			if not pCrawl.children[index]:
				return False
			pCrawl = pCrawl.children[index]

		return pCrawl.isEndOfWord

# driver function
def main():

	# Input keys (use only 'a' through 'z' and lower case)
	keys = ["the","a","there","anaswe","any",
			"by","their"]
	output = ["Not present in trie",
			"Present in trie"]

	# Trie object
	t = Trie()

	# Construct trie
	for key in keys:
		t.insert(key)

	# Search for different keys
	print("{} ---- {}".format("the",output[t.search("the")]))
	print("{} ---- {}".format("these",output[t.search("these")]))
	print("{} ---- {}".format("their",output[t.search("their")]))
	print("{} ---- {}".format("thaw",output[t.search("thaw")]))

if __name__ == '__main__':
	main()

Trie的优点

1. 使用 Trie，我们可以在O(L)时间内插入和查找字符串，其中L表示单个字符串的长度。这显然比 BST 更快。由于它的实现方式，这也比哈希表更快。我们不需要计算任何哈希函数。不需要冲突处理
2. Trie 的另一个优点是，我们可以简单的实现按字母顺序打印字符串，这在哈希表中是不容易做到的。
3. Trie允许我们快速的进行前缀搜索

 其他语言实现下载链接：

（包含各种语言：C、Python、Java、C++、C#、Javascript等均有示例）

免费​资源下载：Trie