对用户的行为进行分析得到用户的偏好后,可以根据用户的偏好计算相似用户和物品,然后可以基于相似用户或物品进行推荐。这就是协同过滤中的两个分支了,即基于用户的协同过滤和基于物品的协同过滤。
关于相似度的计算,现有的几种方法都是基于向量(Vector)的,其实也就是计算两个向量的距离,距离越近相似度越大。
在推荐场景中,在用户-物品偏好的二维矩阵中,我们可以将一个用户对所有物品的偏好作为一个向量来计算用户之间的相似度,或者将所有用户对某个物品的偏好作为一个向量来计算物品之间的相似度。
1.同现相似度
计算公式为:
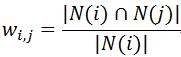
分母|N(i)|是喜欢物品i的用户数,而分子|N(i)∩N(j)|是同时喜欢物品i和物品j的用户数据。
为了防止j为热门物品,修正为:

2.欧式距离相似度
最初用于计算欧几里得空间中的两个点的距离,假设x、y是n维空间的两个点,它们之间的欧几里得距离是:

可以看出,当n=2时,欧几里得距离是平面上的两点的距离。
当用欧几里得距离表示相似度时,一般采用一下公式进行转换:距离越小,相似度越大。

3.Cosine相似度
Cosine相似度被广泛应用于计算文档数据的相似度:
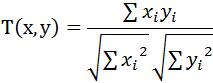




 本文深入探讨了协同过滤算法中的两种主要分支:基于用户的协同过滤和基于物品的协同过滤。通过分析用户行为数据,计算用户和物品之间的相似度,实现个性化推荐。详细介绍了同现相似度、欧式距离相似度和Cosine相似度的计算方法及其在推荐场景中的应用。
本文深入探讨了协同过滤算法中的两种主要分支:基于用户的协同过滤和基于物品的协同过滤。通过分析用户行为数据,计算用户和物品之间的相似度,实现个性化推荐。详细介绍了同现相似度、欧式距离相似度和Cosine相似度的计算方法及其在推荐场景中的应用。
















 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








