大模型Lora微调

xingxiliang

已于 2025-06-17 14:09:40 修改

阅读量1k

点赞数 15

CC 4.0 BY-SA版权

分类专栏：大模型深度学习文章标签： LoRA LLM Transformer

于 2025-06-17 11:47:41 首次发布

本文链接：https://blog.youkuaiyun.com/s_xing/article/details/148711804

大模型同时被 2 个专栏收录

5 篇文章

订阅专栏

深度学习

3 篇文章

订阅专栏

原理

当作增量看待

首先我们可以把新的W，看作老的W + Delta
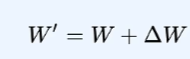
在这里插入图片描述

低秩分解

因为我们只给了少量数据，所以Delta本来就很多0，肯定是一个低秩矩阵。在数学里面所有的低秩矩阵必然可以低秩分解。
在这里插入图片描述

具体的实现

怎样一步一步的计算A和B

初始化

预训练权重 $W$ 保持固定不动（梯度设为 $0$ ）。引入两个可训练的低秩矩阵参数 $A$ 和 $B$ ：

矩阵 $A$ 使用小随机值初始化： $\sim N(0, \sigma^2)$ ，其中 $σ\sigma$ 是一个很小的值。

矩阵 $B$ 初始化为全 $0$ （常用做法）。初始时，参数的增量变化 $ΔW=B×A=0\Delta W = B \times A = 0$ ，因此不会干扰原始模型 $W$ 的输出。

计算损失

输入数据 $X$ 和目标输出 $YtrueY_{\text{true}}$ 。前向传播计算预测输出：

$Ypred=(W+A×B)×XY_{\text{pred}} = (W + A \times B) \times X$

核心概念：原始权重 $W$ 加上低秩更新 $\times B$ 。

根据任务目标（如分类），计算损失函数 $L$ （例如交叉熵损失）：

$\text{Loss}(Y_{\text{pred}}, Y_{\text{true}})$

反向传播更新

通过反向传播算法，计算损失 $L$ 对参数 $A$ 和 $B$ 的梯度：

$∂L∂A,∂L∂B\frac{\partial L}{\partial A}, \frac{\partial L}{\partial B}$

使用优化算法（如梯度下降、Adam）更新 $A$ 和 $B$ ：

$\leftarrow A - \eta \cdot \frac{\partial L}{\partial A}$
$\leftarrow B - \eta \cdot \frac{\partial L}{\partial B}$

其中 $η\eta$ 是学习率（Learning Rate）。

迭代优化

重复执行计算损失和反向传播更新，直至损失函数 $L$ 收敛到满意值或达到预定的训练轮次（epochs）。

最终状态： $A$ 和 $B$ 被优化，使 $\times B$ 适应新任务。原始预训练权重 $W$ 保持不变。

推理方式

合并权重：将 $\times B$ 按缩放系数 $α/r\alpha / r$ 融入 $W$ ，创建新权重 $W^{'}$ ：

$\alpha \cdot \frac{A \times B}{r}$

其中 $r$ 是 LoRA 秩（rank）， $α\alpha$ 是缩放系数（控制更新量强度）。

保持分离：维持 $W$ 、 $A$ 、 $B$ 分离状态，通过加载不同的 $A$ 、 $B$ 快速切换适配不同任务。

核心思想

LoRA 通过训练低秩矩阵 $A$ 和 $B$ 来近似全参数更新 $ΔW\Delta W$ ，即 $ΔW≈B×A\Delta W \approx B \times A$ 。这大大减少了需要训练的参数数量。

应用在transformer的哪些层

并不是每个都需要微调，找到关键的位置去微调
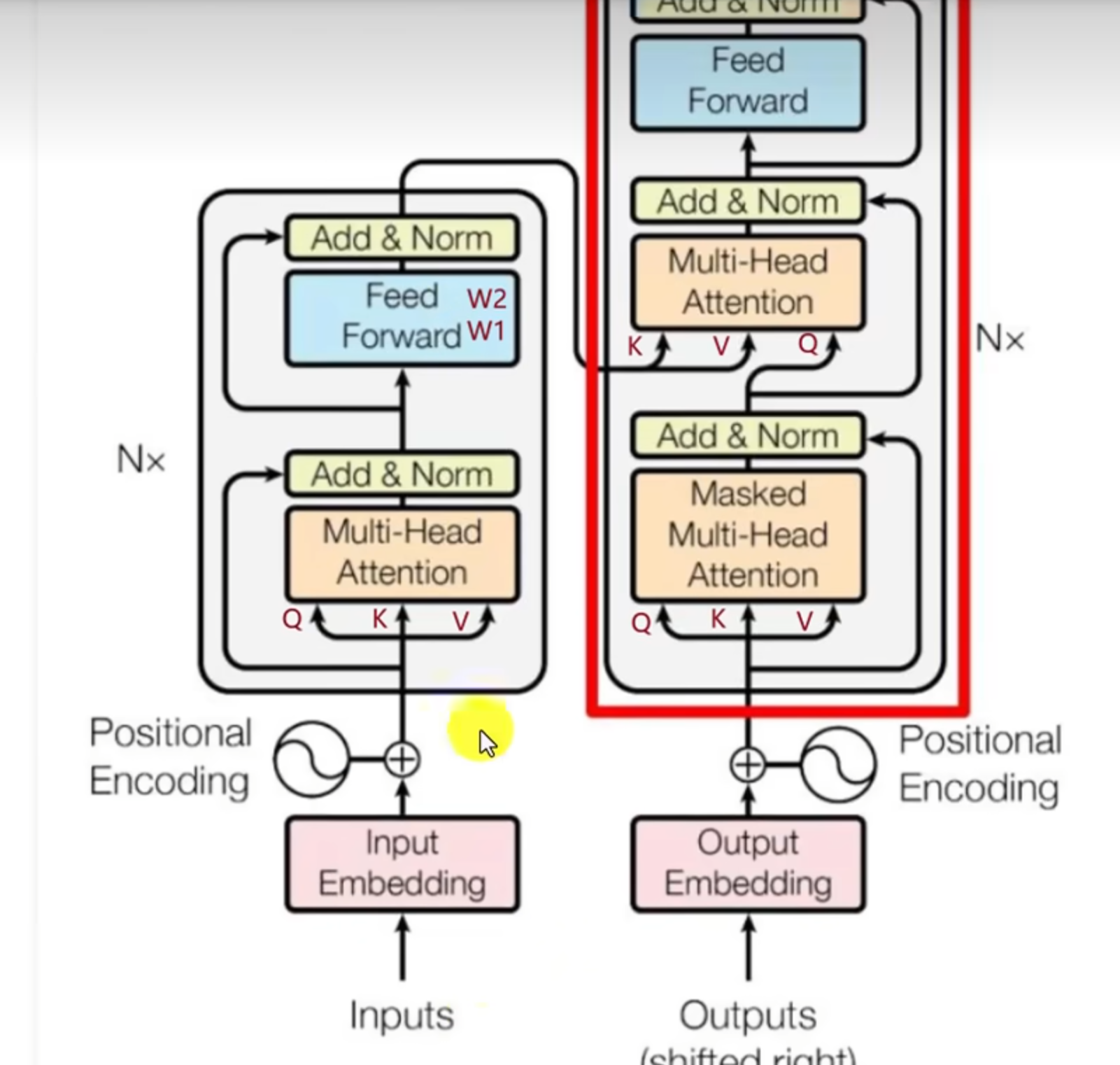
在这里插入图片描述

注意力层（Self-Attention Layer）

LoRA 主要应用于注意力层的权重矩阵。

具体目标矩阵：

查询权重矩阵（W_q）
$Wq′=Wq+Aq×BqW_q' = W_q + A_q \times B_q$
$W_q$ 决定模型关注输入中的哪些信息。
值权重矩阵（W_v）
$Wv′=Wv+Av×BvW_v' = W_v + A_v \times B_v$
$W_v$ 决定输出内容的生成和表达。

选择 W_q 和 W_v 的原因：

微调 $W_q$ 和 $W_v$ 效果接近全参数微调，但训练参数大幅减少。
高性价比：仅调整这两个矩阵即可显著影响模型对任务的理解能力和生成质量。

⚠️ 注意： $W_k$ （键矩阵）和 $W_o$ （输出投影矩阵）通常不应用 LoRA。

前馈层（FFN Layer）

LoRA 可扩展到前馈神经网络（FFN）层中的线性变换矩阵。

目标矩阵：

第一个线性变换（W_1，升维）
$W1′=W1+A1×B1W_1' = W_1 + A_1 \times B_1$
第二个线性变换（W_2，降维）
（逻辑相同，未显式写出公式）

扩展至 FFN 的原因：

FFN 负责特征提取和非线性映射，调整其权重可增强任务特定表达能力。
在大模型（如 GPT-3）或生成式任务中更可能应用，以获得更全面的适配。

实际应用策略：

模型类型	LoRA 应用层建议
小模型（如 BERT）	通常仅应用于注意力层（ $W_q$ , $W_v$ ）
大模型/生成任务	扩展到 FFN 层（ $W_1$ , $W_2$ ）

关键总结

核心层：注意力层的 $W_q$ 和 $W_v$ 是 LoRA 的必选目标，因其直接控制信息关注与输出生成。
扩展层：前馈层（FFN）的 $W_1$ （升维矩阵）可选择性应用，大模型中更常见。
高效性：通过低秩分解（ $\times B$ ），LoRA 仅需训练极少参数即可实现接近全量微调的效果。

讲的挺好的视频教程：https://www.bilibili.com/video/BV1waZ2YDEcp/?spm_id_from=333.337.search-card.all.click&vd_source=82dc2acb60a90c43a2ac0d4023a2cd34

Lora的改进方法

LoRA+ 的基本思路

LoRA+ 是对标准 LoRA（Low-Rank Adaptation）的改进，通过调整不同权重矩阵的学习率，优化模型训练的效率和性能。

核心改进

标准 LoRA 使用固定学习率，而 LoRA+ 提出：

靠近输出的矩阵（B）使用更高学习率（ηB）；
靠近输入的矩阵（A）使用更低学习率（ηA）。

学习率比例定义为：
λ = ηB / ηA
典型范围在 4∼16 之间。

理论依据

改进的动机源于神经网络权重的敏感度分布特性：

靠近输出的权重（B）：直接影响预测结果，对梯度变化更敏感，需要大幅度调整（高学习率）。
靠近输入的权重（A）：承担基础特征提取，需保持稳定（低学习率避免震荡）。

实现方法

典型比例设置：

ηB（B 矩阵学习率）：标准学习率（如 1e-3）；
ηA（A 矩阵学习率）：降低至 ηB / λ（如 λ=10 时，ηA=1e−4）。

相当于赋予 B 矩阵比 A 快 λ 倍的更新速度。

直接效果

训练加速：收敛速度最高提升 2 倍（减少迭代次数）；
性能提升：在相同训练步数下，性能优于标准 LoRA 1%-3%。

LoRA的超参数整理

LoRA微调超参数配置表

超参数名称	数据类型	说明	取值建议	默认值
`finetuning_type`	Literal[“full”,“freeze”,“lora”]	指定微调类型为LoRA	选择`lora`，用于高效微调	`lora`
`lora_alpha`	Optional[int]	缩放系数 $α\alpha$ ，一般情况下为`lora_rank * 2`	设为r的1-2倍，如 $r=16,α=32r=16,\alpha=32$	`None`
`lora_dropout`	float (0.0-1.0)	LoRA的Dropout概率	大数据集: `0.0` 小数据集: `0.05-0.1`	`0.0`
`lora_rank`	int	LoRA的秩 $r$	简单任务: `8-16` 中等任务: `32` 复杂任务: `64+`	`8`
`lora_target`	str (逗号分隔)	应用LoRA方法的模块名称	默认: `q_proj,v_proj` 复杂任务加`k_proj,o_proj`或FFN	`all`
`additional_target`	str (逗号分隔)	额外的LoRA目标模块	通常留空，除非有特殊模块	`None`
`loraplus_lr_ratio`	Optional[float]	LoRA+学习率比例( $λ=ηB/ηA\lambda=\eta_B/\eta_A$ )	启用时设`4-16` (如`8`)	`None`
`use_rslora`	bool	是否启用秩稳定LoRA(rsLoRA)	小 $r$ (`4-16`) : `false` 大 $r$ (`32+`) : `true`	`false`
`use_dora`	bool	是否启用权重分解DoRA	默认`false`，复杂任务开启	`false`
`pissa_init`	bool	是否用PiSSA初始化LoRA (注：PiSSA = Power Iteration SVD Stablization Algo.)	默认`false`，需高性能时设`true`	`false`

目标模块选择

q_proj: 查询投影层，适用于需要调整查询机制的模型任务
v_proj: 值投影层，默认必选模块，影响模型的核心输出
k_proj: 键投影层，建议在复杂任务中添加以增强模型性能
o_proj: 输出投影层，复杂任务中推荐使用以优化最终结果
FFN: 前馈网络层，大模型或复杂任务中建议添加

进阶技术

LoRA+: 通过设置差异学习率（λ=η_B/η_A，η_B > η_A）实现高效微调
rsLoRA: 针对大秩任务（r≥32）的秩稳定优化技术
DoRA: 权重分解技术，显著提升复杂任务的表现能力
PiSSA: 基于幂迭代SVD的初始化方法，加快模型收敛速度

典型配置示例

# 中等复杂度任务配置  
config = {  
    "lora_rank": 32,  
    "lora_alpha": 64,  
    "lora_target": "q_proj,v_proj,o_proj",  
    "lora_dropout": 0.05,  
    "loraplus_lr_ratio": 8  # 启用LoRA+  
}