对数图像、极坐标图像、柱状图、散点图、3D图像简单绘制

对数图像函数

对数函数绘制设计三个函数，解析如下：

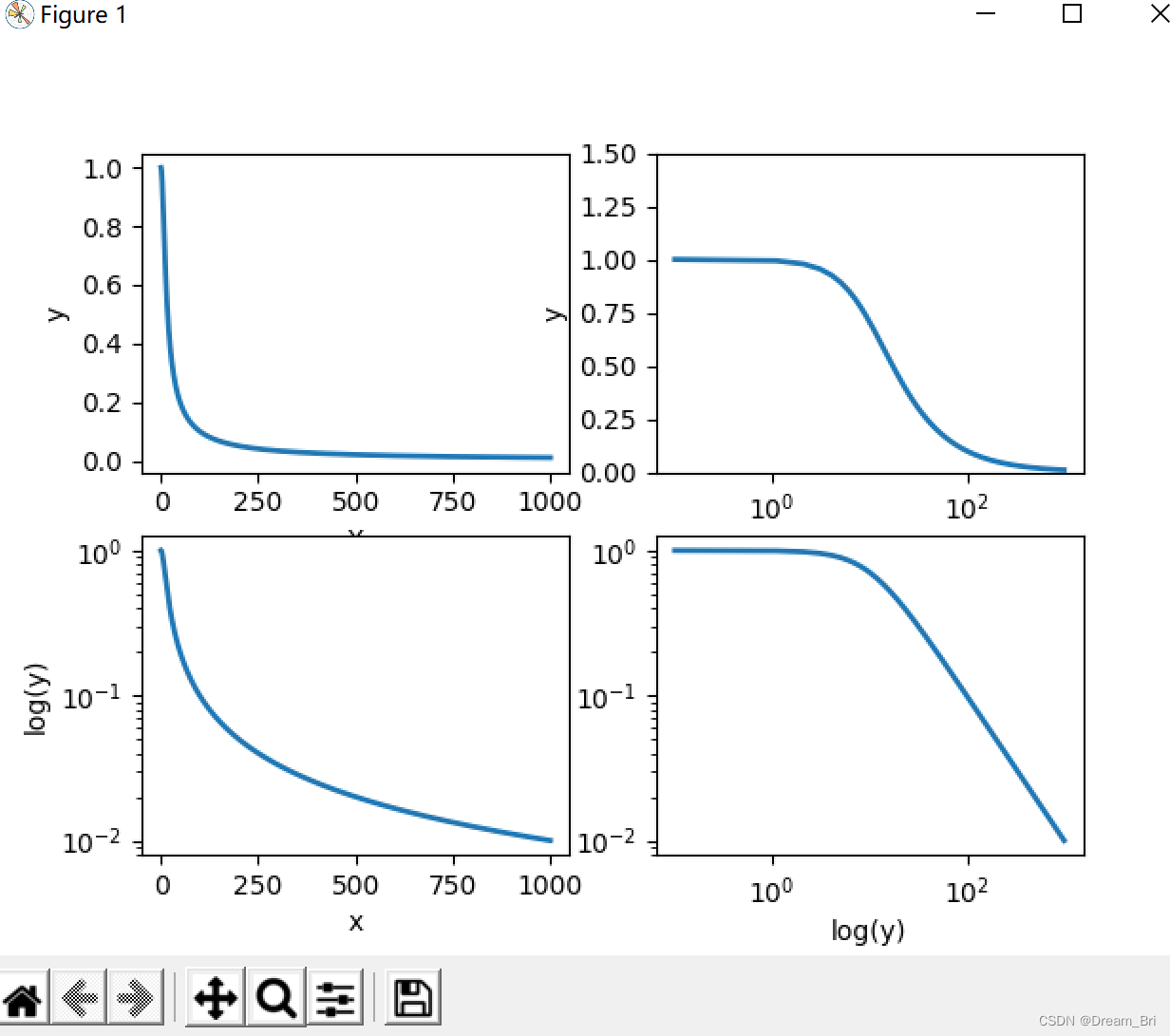
semilogx(x1, y1)：半对数函数，x变为常用对数刻度，y轴仍是线性刻度。

semilogy(x1, y1)：半对数函数，x仍是线性刻度，y轴变为常用对数刻度。

loglog(x1, y1)：全对数函数，x，y都变为常用对数刻度。

代码显示如下：

import numpy as np
import matplotlib.pyplot as plt

w = np.linspace(0.1, 1000, 1000)
p = np.abs(1 / (1 + 0.1j * w))

plt.subplot(221)
plt.plot(w, p, lw=2)
plt.xlabel('X')
plt.ylabel('y')

plt.subplot(222)
plt.semilogx(w, p, lw=2)
# ylim具有设置y坐标轴范围的作用
plt.ylim(0, 1.5)
plt.xlabel('log(X)')
plt.ylabel('y')

plt.subplot(223)
plt.semilogy(w, p, lw=2)
# plt.ylim(0, 1.5)
plt.xlabel('x')
plt.ylabel('log(y)')

plt.subplot(224)
plt.loglog(w, p, lw=2)
plt.xlabel('log(x)')
plt.xlabel('log(y)')
plt.show()

显示结果如下：

极坐标图像显示

代码显示：

import numpy as np
import matplotlib.pyplot as plt

theta