如何求两个信号的相位差

1.
在信号处理里经常会碰到，用于相位差的非参数估计，我接触到的典型的用处就是在ISAR成像中用于平动相位估计。

假设两个频率相同具有相位差的信号

其时间互相关函数为


相位差

% test programme for phase error estimation
clc; clear;

%% Signal
f0 = 200; % signal frequency (Hz)
fs = 1000; % sampling frequency (Hz)
T = 5 / f0; % sampling time (s)
N = round(T * fs);
N = N + mod(N, 2);
t = [0: N - 1] / fs;

phase_1 = pi * rand(1, 1);
phase_2 = pi * rand(1, 1);
phase_error = phase_1 - phase_2
s1 = exp(1i * 2 * pi * f0 * t + 1i * phase_1);
s2 = exp(1i * 2 * pi * f0 * t + 1i * phase_2);

%% Phase error estimation
corr = xcorr(s1, s2); % cross-correlation function
corr_abs = abs(corr);

phase_error_estimated = angle(corr(corr_abs == max(corr_abs)) / abs(corr(corr_abs == max(corr_abs))))

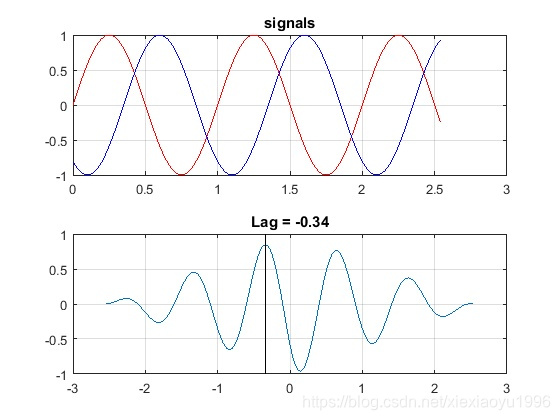
2.一个简单的办法是构造一个没有lag的，频率相同的标准信号。然后做两者的cross-correlation, 然后找出最大的Lag, 看它对应的时间点是什么。

举例来说
比如你有信号s2, 延时是0.35s（相位差为2pi.35 那么你可以构造一个0相位的s1

t = [0:127]0.02;
f = 1.0;
s1 = sin(2pift);
s2 = sin(2pif*(t-0.35));

做cross-correlation

x = xcorr(s1,s2,‘coeff’);
tx = [-127:127]*0.02;

x的最大值那点所对应的横坐标(tx)就是延时。

3.
两个信号分别与cos(2πft)和sin(2πft)做内积，结果记为X1,Y1；X2,Y2
求出real和imag 使用atan2（real，imag）求得相位
atan2(Y1,X1) 和 atan2(Y2,X2)分别是两个信号的绝对相位，取值范围是 (-π,π]
把绝对相位做差得到相对相位

4.
% H=hilbert(x);%Hilbert变换
% ang=angle(H) %求折叠相位 ，这个就是瞬时相位

**5.**另有：Z为一个复数时，R=abs(Z)，theta=angle(Z),之后利用Z=R.exp(itheta)可以将Z复原.