操作系统：进程调度

操作系统：进程调度的设计与分析

---

一、目的

多道程序设计中，经常是若干个进程同时处于就绪状态，必须依照某种策略来决定那个进程优先占有处理机。因而引起进程调度。本实验模拟在单处理机情况下的处理机调度问题，加深对进程调度的理解。

---

二、内容

1、优先权法、轮转法

简化假设

1）进程为计算型的（无I/O）

2）进程状态：ready、running、finish

3）进程需要的CPU时间以时间片为单位确定

2、算法描述

1）优先权法

2）轮转法

---

三、要求

1、优先权法和轮转法的优先级、到达时间、服务时间随机生成。

2、完成时间、周转时间、带权周转时间、平均周转时间、平均带权周转时间全表格生成。

3、实现图形化演示；

4、对算法进行不改变基本定义之上的提升改进

---

四、注意事项

1．如采用随机数，随机数的取值范围应加以限制，如所需的CPU时间限制在1~20之间。

2．进程数n不要太大通常取4~8个

3．二种调度算法

4．若有可能请在图形方式下，将PCB的调度用图形成动画显示。

---

五、分析过程

下面分别来对“优先权法”和“RR 轮转法”来进行算法的简单描述。以及整个实践过程的流程图：

1. 对“优先权算法"过程描述：

• 首先再运行到优先权算法的时候，就表明了这个进程的数组（动态的生成）已经按照进程的到达时间（arriveTime）进行了非降序排列，我们把这个数组暂时成为原始数组也就是process[]。

• 那么第二步就是怎么实现进程按照先到者服务，如果后到的进程优先级更低，发生强占。那么这个过程的本质其实是按照优先级去进行 cpu 的调度，我的方法就是，在整个 time 时间的跳动下(for循环)中，来依次判断有没有进程的到达，如果有，我们就将其放入一个新的数组中，这里称之为优先级数组(Process_Priority_Array[])；

• 这个时候我们在这个time遍历中就每次判断这个优先级数组中有没有进程的剩余服务时间serviceTime是非零的辅助函数bool isAllZero(Process* ProcessArray, int size) ；

• 如果有，那么就从第一个非零服务时间的进程int firstIsNotZero(Process* ProcessArray, int size) 辅助函数开始调用CPU。
  也就是该进程的serviceTime--，然后判断这个进程的剩余服务时间是否变为0，如果变为零，就记录一下运行完成的进程数量finishNumbers),且更新这个服务完的进程的完成时间finishTime；如果剩余服务时间还有，这个时候就正常再进行time 遍历，这就保证了优先级的强占的过程。

• 最后，如果当记录的完成进程的数量==进程的个数(随即生成)，这个时候就跳出 time 遍历，代表所有的进程都完成了，时间也就不必再跳动了

---

2. 对“RR 轮转法算法”描述：

• 轮转法就相对比较简单，就是一个队列就进出和出队元素是否还要回到队列的问题，那我们就用队列的方式来实现算法的描述，且也用string二维数组来对其进行输出，展现一线法的表现形式。
• 首先定义一个rocess型的队列queue<Process>RR_queue;，同样也是在时间 time 的遍历下，如果有进程到达，就进入队列，这是就运用一个辅助函数void input_Process_RRArray(queue<Process>& RR_queue, int time, string** RR_arr, int R, Process* RR_pro, int size, int& finishNumbers)用来对当前时刻 time 的情况，对队首进程来判断是否结束，还需要回到队尾吗？同时如果结束了当前进程，就将finishNumbers++，并将队列的进程按照一线法的形式添加到二维数组中即可。
• 最后，同样的，如果当记录的完成进程的数量==进程的个数(随即生成)，这个时候就跳出 time 遍历，代表所有的进程都完成了，时间也就不必再跳动了

---

3. 关于优先级调度算法的改进：

动态的调整进程的优先级，避免先到达的低优先级进程因为等待时间而长时间处于饥饿状态，主要思想：每个时间都对进程进行优先级的动态调整，调整思路：对已经等待的时间和进程剩余的服务时间加权，如果等待的时间越长，那么优先级高（数值越小），如果剩余服务时间长，那么优先级越低，保证短作业可以先完成，公式：

newpriority=newpriority - 0.5 * waitTime + 0.5 * remain_servicesTime;

为什么两个都是0.5，因为尝试过许多加权数据，两个0.5在测试10次输出的时候效果是最好的，即保证了短作业可以尽快完成，又保证了进程等待时间长了也可以得到补偿，避免长时间处于饥饿状态

---

4. 流程图：
   优先级调度算法：
   

---

轮转法

---

六、必要说明以及问题分析

首先为什么要用 .hpp 文件，因为开始的时候是用一个Process.cpp和Process.h加一个main.cpp来完成的，但是考虑到可能要使用类模板来写模板函数，类模板函数的实现与声明不能分开写，而且将函数声明和函数实现分开写，对于我的程序中要利用的函数太多，看起来就会比价杂乱，所以改写.hpp文件

---

准备工作和优先权算法的问题和说明：

1、随机数生成好了以后要验证输出，我先想到的是写一个print()函数，再到主函数中用for循环输出。

但是这会让for循环中的cout输出链式结构输出其他内容的时候又要单独换行处理，不方便，所以**重写运算符左移符号**

2、在重写运算符左移符号后，虽然里面的程序加上了’\t’，

但是输出的时候还是会因为服务时间和优先级的数字位数不一样，导致制表位就算后移了一位还是出现输出不整齐的情况，所以查资料加上了运用了 setw()。

3、对于优先权算法，我首先想到的是用队列的形式，但是因为对于<queue>不能对中间插入元素，只能处理首尾元素，很明显这就不符合我们的需求；其次就是因为要对进程到达，优先级和还剩的进程服务时间综合考虑，可能一个简单的队列就难以解决。

4、在优先权算法中，在标记一个进程的结束时间后，没有考虑到在同一时刻也会有另外一个进程正在开始进行,所以在记录到达后不能马上跳到时间递增上，而是要判断是不是还有进程在执行，同样只要是调用 cpu 的进程处理一次服务时间以后就需要判断是否做结束处理。

5、在优先权算法中，整体的思想是从原来按照到达时间排序后的数组来再按照优先权排序来依次处理，为什么还要修改原数组：因为最后的表格输出是从原数组来输出对应的结束时间，周转时间和带权周转时间。所以进程运行完了到了结束时间，就不好回去再找到原来数组中相应进程的位置来标记时间了。

• 方案1：这个时候我就在定义了一个自用的变量my_val,用来对两个数组中的进程位置关系做了一个对应，这样就可以回到原来的排序数组中找到进程给进程标记上结束时间了。
• 方案2：上面的方案代码就比较冗杂，所以后面用了while 循环去查找原数组中对应的进程。
• 方案3：其实最方便的方法是将其结束时间这个属性写成指针的形式，这样即使在优先级数组中修改了进程的结束时间，那么原数组也会被修改，但是没用这个方案，因为这是我在最后想到的，如果要修改那就要修改拷贝构造函数以及大量的代码，其次就是如果用指针的形式，那么就代表了进程的结束时间只有一份，那么后面的RR轮转法和改进的算法用的也是这一份地址，最后如果是顺序输出三个算法不会出现问题，但是如果想测试其中的某个算法，那么数据就会受到污染，其实也不方便，所以还是用了方案二。

---

RR 轮转法中遇到的问题和说明：

6、在 RR 轮转法中，在一个时间时刻，有进程到达，那么是先将这个进程移动到队列中，还是先让这个时刻调度完的进程回到队尾呢？按照上课的方法，应该是先让到达的进程进入队尾

再继续判断这个时刻到下一个时刻的时间段期间，比如，现在是 4 时刻，队列中有 A B，那么 C 在这个时刻到达，应该先让 C 进入这个队列，再处理 4~5 这个时间段队列的状态。

7、在RR 轮转法的辅助函数RR_Scheduling_help()中，将进程放入二维数组的函数中，我开始是用for循环，范围是0-size-1,但是没有考虑到就是该开始进程并没有全部到达那么范围就不是 size -1 的时候会超出队列的范围，

所以应该以队列是否为空来判断，应该用 while 循环。

8、还是RR_Scheduling_help()函数中，开始我就先拷贝了一份原队列，虽然在处理原队列的时候都判断队列是否为空，但是我用到拷贝队列的时候，我就默认先移除了拷贝队列的队头元素，没有考虑是不是也是空的状态。

导致引发 x00007FFB9806829C (ucrtbased.dll)处有未经处理的异常: 将一个无效参数传递给了将无效参数视为严重错误的函数。所以，在最开始就判断传入的队列是不是空的，如果是就直接返回！

9、开始我两个调度算法都是用的同一个进程数组 process[],但是在后面 RR 轮转法更新了数组中每个进程的结束时间后，前面的优先权法更新的数据也会受到影响，所以解决方法就是：

在开始创建的 process[] 数组只用来输出开始的数据表格，再拷贝两份这个数组process[]，各自用于两个调度算法，这样就不会相互影响。包括后面的算法改进，同样拷贝数组，保证数据源不受污染，每个算法都使用单独的数组来实现。

10、因为开始时候都是在进程初始为 5 的静态进程数组中来实现，一开始先用静态数组简单的实现算法，到最后我改用动态的 Process * p = new Process[size] 来实现动态的随机进程情况，由于在所有的函数中，都用的是 size 而不是 5，所以函数不用做其他修改，但是其实更好的办法使用容器，这样既可以避免指针释放的问题，又动态实现进程的管理，我将在改进算法中尝试使用 <容器> + <algorithm> 来具体改进。

11、在输出检查的过程中发现了一个比较严重的错误，有进程的带权周转时间小于 1，后面发现原因以后是因为结束时间的设置错误，比如一个优先级最高的进程到达时间为 1，服务时间为 3，那么我开始认为其占用 cpu 的时间是 1，2，3，则 3 结束，那么这个时候结束时间 – 到达时间则 = 3-1=2；明显这是错误的。

解决：其实解决也比较简单，结束时间的设置应该是在该时间点的末尾，也就是下一个时间点的开始，所以其实需要向后移动一个时间点再记录结束时间，就可以解决这个问题。

---

改进算法中遇到的问题和说明：

12、改进想法：动态的调整进程的优先级，避免先到达的低优先级进程因为等待时间而长时间处于饥饿状态。为了更好的表示改进算法的实现，再添加三个属性：waitTime,newpriority, remain_servicesTime;

刚开始的改进思路：如果一个进程的等待时间大于其总服务时间，就调整其为最高优先级。用 <map> 来实现改进思路， 将 map 的 key 值作为进程的优先级值，value 值作为Process 数据类型，因为 map 会按照 key 值自动排序，这样就可以实现优先级调度优先。

• 问题 1：如果动态调整一个进程的优先级变为 1 ，那这个时候原本的 1 优先级到达了，就会冲突。解决：所以再动态调整优先级的时候，应该将其他的进程（无论到达与否）的优先级全部后移一位，以免冲突。

• 问题 2：但是很快就出现较为严重的问题：发现如果修改了进程的优先级，就要修改 map 的 key 值，但是 map 的实现是二叉树，修改 key 会造成数结构混乱的问题，所以我们还是用回 vector 加上排序算法来进程算法改进。

• 问题 3：用了 vector 容器以后在优化优先级的过程中遇到的问题：如果我们只是单纯的按照（等待时间>=剩余服务时间 && 等待时间>=3）来判断,仅仅将这个进程移动到优先级最高，其他的进程优先级后移，这样单纯的改进其实是低效无用的：

在运行的时候十次一半会发生改进后的算法的平均带权周转时间还比原来的算法要高，所以反思考虑到只是单纯的按照这个条件来使得原本低优先级的进程变成了高优先级的进程，而没有多次的调整，导致原本优先级高的进程也会处于长时间的饥饿状态。

其次就是这个等待时间是怎么来评价？是在进程的上一次调用以后的等待时间吗？还是总的等待时间？如果是总的等待时间，那么这个 >=3 将意义不大。

解决：等待时间应为进程从到达开始到当前时间下没有调用 cpu 的时间总和，这样可以避免有些进程发生反复等待一段时间又被新来的优先级强占的情况；其次，我们要综合考虑到进程的等待时间和剩余服务时间，先让短作业的进程优先，剩余服务时间少的等待时间长的进程分别赋予权重，来实时的调整各个进程的优先级。

最终方案：每个时间都对进程进行优先级的动态调整，调整思路：对已经等待的时间和进程剩余的服务时间加权，如果等待的时间越长，那么优先级高（数值越小），如果剩余服务时间长，那么优先级越低，保证短作业可以先完成，公式：

ewpriority=newpriority - 0.5 * waitTime + 0.5 * remain_servicesTime;

为什么两个都是0.5，因为尝试过许多加权数据，两个0.5在测试10次输出的时候效果是最好的，即保证了短作业可以尽快完成，又保证了进程等待时间长了也可以得到补偿，避免长时间处于饥饿状态。

---

对于程序算法的一些思考

实验中暂无未解决的问题，但对程序有一些反思：

1. 代码的复用率低：

快速排序 QuickSort() 硬编码为 Process 类服务，未使用模板或通用设计，后期难以扩展。随机数生成、printFrom()这样类似的函数功能可封装为工具类，减少重复代码。

2. 内存管理风险：

虽然在最后都对指针进行了处理，但是如果中间过程出错，指针堆积在末尾释放就可能出现问题，可以学习智能指针加以改进或使用容器来封装继承。

3. 改进算法可能不太完善

动态优先级调整函数adjust_Priority()中公式计算：newpriority=newpriority - 0.5 * waitTime + 0.5 * remain_servicesTime; 大概率会出现相同优先级的进程，其实没有过多的考虑其中优先级重复怎么办，可能会有违背优先级调度算法的设计初衷。

---

运行近20遍代码，发现如果生成的短作业较多，而且优先级比较低，那么优先级调度算法的平均带权周转时间会==高于轮转法和改进后的优先级调度算法；如果生成的短作业较少，那么优先级调度算法平均带权周转时间明显低于==轮转法，而改进后的优先级调度算法也几乎每次都可以减少平均带权周转时间，证明了改进后的算法确实优化了算法。

但是并不是每次的输出都是改进后的优先级调度算法优于改进前的，所以证明这个改进并不是一个最周全的改进。

场景	优先级调度 (PS)	轮转法 (RR)	改进优先级调度 (DPS)	结论
短作业多+低优先级	较高	较低	较低	DPS有效缓解短作业饥饿问题
短作业少	最低	较高	接近或略优于PS	DPS在长作业场景无显著副作用

七、附录

核心代码

首先是一些准备工作

/******************************************************************************************************************/
// 一些准备工作：
/******************************************************************************************************************/

// 随机数生成函数辅助函数，检查重复随机数的函数
bool isRandBeUsed(int priority, int* pro, int size) {
	for (int i = 0;i < size;i++) {
		if (pro[i] == priority) {
			return true;
		}
	}
	return false;
}

// 生成不重复的 1-size 随机数数组
int* getUniquePriority(int size) {
	int* pri = new int[size];
	for (int i = 0;i < size;i++) {
		pri[i] = 0;
	}
	int priority, i = 0;
	while (i < size) {
		priority = rand() % size + 1;
		if (!isRandBeUsed(priority, pri, size)) {
			pri[i] = priority;
			i++;
		}
	}
	return pri;
}

// 生成 1-size*2 之内的进程到达时间数组
int* getArriveTime(int size) {
	int* arr = new int[size];
	for (int i = 0;i < size;++i) {
		arr[i] = rand() % (size * 2) + 1;
	}
	return arr;
}

// 生成 1-10 之间的 cpu 调用时间数组
int* getServiceTime(int size) {
	int* ser = new int[size];
	for (int i = 0;i < size;++i) {
		ser[i] = rand() % 10 + 1;
	}
	return ser;
}

// << 运算符重载，方便输出process类
ostream& operator<<(ostream& out, Process p) {
	out << "arriveTime : " << setw(2) << p.arriveTime << '\t';
	out << "serviceTime : " << setw(2) << p.serviceTime << '\t';
	out << "priority : " << setw(2) << p.priority << '\t';
	return out;
}

// 给进程数组中的成员赋值
void addVal(Process* process, int size, int* arr, int* ser, int* pro) {
	// 给进程类的数组的成员属性赋值
	for (int i = 0;i < size;i++) {
		process[i].name = static_cast<char>('A' + i);
		process[i].arriveTime = arr[i];

		process[i].serviceTime = ser[i];
		process[i].remain_servicesTime = ser[i]; // 改进部分需要用到

		process[i].priority = pro[i];
		process[i].newpriority = pro[i]; // 改进部分需要用到
	}
}

// 利用快速排序来针对进程的 **到达时间** 将 Process 对象进行非降序排序，
// 因为是数组的形式存放进程对象，所以排序比较麻烦，在后面的优先级算法改进中我们将用 vector + sort
int Partition(Process* pro, int first, int last) {
	int i = first, j = last;
	while (i < j) {
		while (i < j && pro[i].arriveTime <= pro[j].arriveTime) j--;
		if (i < j) {
			pro[i++].exchange(pro[j]);
		}
		while (i < j && pro[i].arriveTime <= pro[j].arriveTime) i++;
		if (i < j) {
			pro[i].exchange(pro[j--]);
		}
	}
	return i;
}

// 递归快速排序左右区间
void QuickSort(Process* pro, int first, int last) {
	if (first >= last) return;
	else {
		int pivot = Partition(pro, first, last);
		QuickSort(pro, first, pivot - 1); // 对左区间进行快速排序
		QuickSort(pro, pivot + 1, last); // 右区间
	}
}

// 表格形式输出开始时候的进程的到达时间，服务时间和优先级的情况
void printForm(Process* pro, int size) {
	// 输出表头
	cout << "——————————————————————————————————————————————————————" << endl;
	cout << left << "|" << setw(10) << " process" << "| " << setw(10) << " priority"
		<< "| " << setw(15) << " arriveTime" << "| " << setw(11) << "serviceTime" << "|" << endl;
	cout << "——————————————————————————————————————————————————————" << endl;

	// 外层循环遍历每个进程（行）
	for (int i = 0; i < size; i++) {
		// 内层循环遍历每个进程的属性（列）
		cout << left; // 保证对其，包括下面的swtw()中的参数，都是在输出结果中调整后取最合适的参数形成表格
		cout << "|    " << setw(6) << pro[i].name;
		cout << "|    " << setw(7) << pro[i].priority;
		cout << "|        " << setw(8) << pro[i].arriveTime;
		cout << "|     " << setw(7) << pro[i].serviceTime << "|" << endl;
		cout << "——————————————————————————————————————————————————————" << endl;
	}
}

/******************************************************************************************************************/
// 到此，准备工作完成！
/******************************************************************************************************************/

---

优先级调度算法

/************************** 优先级调度算法：***************************/
/*********************************************************************/
// 进程调度具体函数(算法的辅助函数)
void pri_scheduling_help(Process* priority_pro, int index, string** arr, Process* Process_Priority_Array, int size, int time, int& finish_Numbers) {
	for (int i = 0;i < size;++i) {
		if (i == index) {
			arr[index + 1][time] = "-";

			// 如果这次时间结束进程的服务时间变成 0 ，说明进程结束，则在下一个时间点标记 F 表示结束
			if (--Process_Priority_Array[i].serviceTime == 0) {
				arr[index + 1][time + 1] = "F";

				// 找到原进程数组中对应的进行 和 当前的优先级数组 同样都添加结束时间
				int j = 0;
				while (priority_pro[j].name != Process_Priority_Array[index].name) j++;
				priority_pro[j].finishTime = time + 1;

				Process_Priority_Array[i].finishTime = time + 1;
				finish_Numbers++;

				// cout << "Time " << time << ": Process " << Process_Priority_Array[i].name << " finished." << endl;
			}

		}
		// 其他的进程都处于等待的过程, * 在二维数组中表示等待
		else if (Process_Priority_Array[i].serviceTime > 0) {
			arr[i + 1][time] = "*";
		}
	}
}

// 优先级调度核心算法：
// 参数： priority_pro 按到达时间排序后的进程数组；size 数组长度；arr 为需要输出的二维数组； R C 二维数组的行列；
void priority_algorithm(Process* priority_pro, int size, string** arr, int R, int C) {
	int time = 1;
	int n = 0; // 进程到达的个数
	int finish_Numbers = 0; // 进程结束的个数

	// 创建一个由优先级来存放进程的数组
	Process* Process_Priority_Array = new Process[size];

	for (;time < C;time++) {

		// 处理当前时间到达的进程
		// 可能存在多个进程到达的情况
		while (n < size && time == priority_pro[n].arriveTime) {
			int priority = priority_pro[n].priority - 1;

			// 按优先级放到优先权数组中对应的位置
			Process_Priority_Array[priority] = priority_pro[n];

			// 在二维数组表中记录
			arr[priority + 1][0] = priority_pro[n].name;
			n++; // 继续下一个进程
		}

		// 找到从优先级数组中遍历的第一个未完成的进程 (具体实现在"附录")
		int i = firstIsNotZero(Process_Priority_Array, size);

		// 数组中还有未结束的进程
		if (i != -1) {
			// 调用进程调度的函数
			pri_scheduling_help(priority_pro, i, arr, Process_Priority_Array, size, time, finish_Numbers);
		}
		// 说明数组中所有进程的结束了，如果结束进程的数量等于进程数量，就结束算法，否则说明这个时刻 cpu 空闲
		else if (finish_Numbers == size) {
			break; //表示所有进程都结束了，就不需要再跳动时间了
		}
	}
	C = time + 1; // 更新二维数组的列数，以免输出的时候避免不必要的空列数

	// 初始化二维数组列表的第一行,显示为时间
	for (int t = 1;t < time + 1;t++) {
		arr[0][t] = to_string(t);
	}
	delete[] Process_Priority_Array;
}

/******************************************************************************************************************/
// 到此，就实现了优先权的调度算法！
/*******************************************************************************************************************/

---

轮转法

// 下面，来实现RR轮转法。因为有许多的函数确实是可以重复利用的比如isAllZero()、firstIsNotZero()等，但是为了能尝试松散耦合高内聚，我尝试重写一些函数，保证能更好的适用于RR轮转法
/*
主要思路：RR 轮转法只会用到进程的达到时间和服务时间来考虑问题，所以这个时候在一线法的基础上用队列的形式来实现是比较好的
		为了实现一线法的效果，还是用二维数组来实现整个过程
*/

/************************* RR 轮转算法：***************************/
// RR 轮转法的辅助函数：
// 参数说明：RR_queue：进程队列；time 当前时间；RR_arr 需要数组的数组(二级指针)；size 为 pro[] 的长度；finishNumbers 完成的进程个数；
void RR_Scheduling_help(queue<Process>& RR_queue, int time, string** RR_arr, int R, Process* RR_pro, int size, int& finishNumbers) {
	if (RR_queue.empty()) {
		return;
	}

	// 拷贝队列，那么二维数组中的添加情况就只用依次读取和移除临时队列的首进程即可
	queue<Process> temp_q = RR_queue;

	// **先对队头进程处理**
	if (!RR_queue.empty()) {
		RR_arr[0][time] = RR_queue.front().name;
		RR_queue.front().serviceTime--;
		Process frontProcess = RR_queue.front(); // 先记录队头进程

		// 判断队头进程经过这个时间片后剩余服务时间是否为零
		if (frontProcess.serviceTime > 0) {
			RR_queue.pop();
			RR_queue.push(frontProcess); // 还有剩余服务时间，再回到队尾，否则移除队列
		}
		else {
			for (int i = 0;i < size;i++) {
				// 遍历原进程数组，找到当前 time 结束的进程并更新其结束时间
				if (RR_pro[i].name == RR_queue.front().name) {
					RR_pro[i].finishTime = time + 1;
					RR_queue.pop(); // 并移除已经结束的进程
					finishNumbers++;// 表示结束的进程数 +1 
					break;
				}
			}
		}
	}
	// **处理剩下的进程**
	temp_q.pop(); // 只用处理剩余的进程即可
	int i = 4; // 因为二维数组第 123 行放时间片和分割线了，所以从第 4 行继续填入进程
	while (!temp_q.empty() && i < R) {
		RR_arr[i][time] = temp_q.front().name;
		temp_q.pop();
		i++;
	}
}

// 参数说明：RR_pro：按到达时间排序后的进程数组；size 数组长度；RR_arr 为需要输出的二维数组； R C 二维数组的行列；
void RR_Scheduling_algorithm(Process* RR_pro, int size, string** RR_arr, int R, int C) {
	int time = 1;
	int n = 0; // 同样也是进程到达的个数

	// 进程结束的个数，用于避免输出最后过多的无用时间
	int finishNumber = 0;

	queue<Process>RR_queue;
	for (;time < C;time++) {

		// 如果这个时刻有进程到达，那么就先将其添加到队尾
		// while 循环考虑到可能有多个进程一起到达的情况
		while (n < size && RR_pro[n].arriveTime == time) {
			RR_queue.push(RR_pro[n]);
			// cout << "Time " << time << ": Process " << RR_pro[n].name << " 到达" << endl;

			n++; // 处理后续进程

			if (n == size) {
				cout << endl; // 输出换行，不影响下面输出的一线法
				cout << "************************ 以下是一线法的过程展示：***************************" << endl << endl;
			}
		}

		// RR 轮转法的辅助函数
		RR_Scheduling_help(RR_queue, time, RR_arr, R, RR_pro, size, finishNumber);
		if (finishNumber == size) {
			break; // 表示所有进程都结束了，此时就不用再跳动时间了
		}
	}
	C = time + 1;
	for (int t = 1;t < C;t++) {
		// 一线法的展示效果，第1行显示时间，第0行显示正在服务的进程，用"-"分隔开，下面是队列进程
		RR_arr[1][t] = "-";
		RR_arr[2][t] = to_string(t);
		RR_arr[3][t] = "-";
	}
}
/******************************************************************************************************************/
// 到此，就实现了 RR 轮转法！
/*******************************************************************************************************************/

改进的优先级调度算法

// 改进优先级调度算法：动态优先级
// 参数：按照优先级高低顺序存放进程的数组；数组长度；需要输出的二维数组；二维数组的行和列
void  priority_algorithm_Impront(Process* priority_pro, int size, string** arr, int R, int& C) {

	// Process* 容器，存放进程的地址，这样在容器中更新进程的优先级那么原数组也可以得到变化
	vector<Process*> vector_Process;

	int time = 1;
	int n = 0; // 进程到达的个数
	int finish_Numbers = 0; // 进程结束的个数

	for (;time < C;time++) {
		while (n < size && time == priority_pro[n].arriveTime) {
			vector_Process.push_back(&priority_pro[n]);

			// 按照优先级排序 Process容器
			sort(vector_Process.begin(), vector_Process.end(), compareVectorProcess());
			arr[priority_pro[n].priority][0] = priority_pro[n].name;

			n++;
		}
		// 调整进程的优先级，*** 关键 ***
		adjust_Prioriry(vector_Process, priority_pro, size);

		// 找到优先级最高且还有服务时间的进程
		auto it = find_if(vector_Process.begin(), vector_Process.end(), firstNoFinish());

		if (it == vector_Process.end()) {
			if (finish_Numbers == size) break; // 说明目前容器中所有的进程都完成了调度
			continue; // 否则回到 while 循环继续
		}
		else {
			// 进程调度的函数：填充二维数组以输出(附录)
			scheduling(vector_Process, it, arr, time, finish_Numbers);
		}
	}
	C = time + 1; // 更新二维数组的列数，以免输出的时候避免不必要的空列数
	for (int t = 1;t < time + 1;t++) { // 初始化二维数组列表的第一行,显示为时间
		arr[0][t] = to_string(t);
	}
}

程序结果

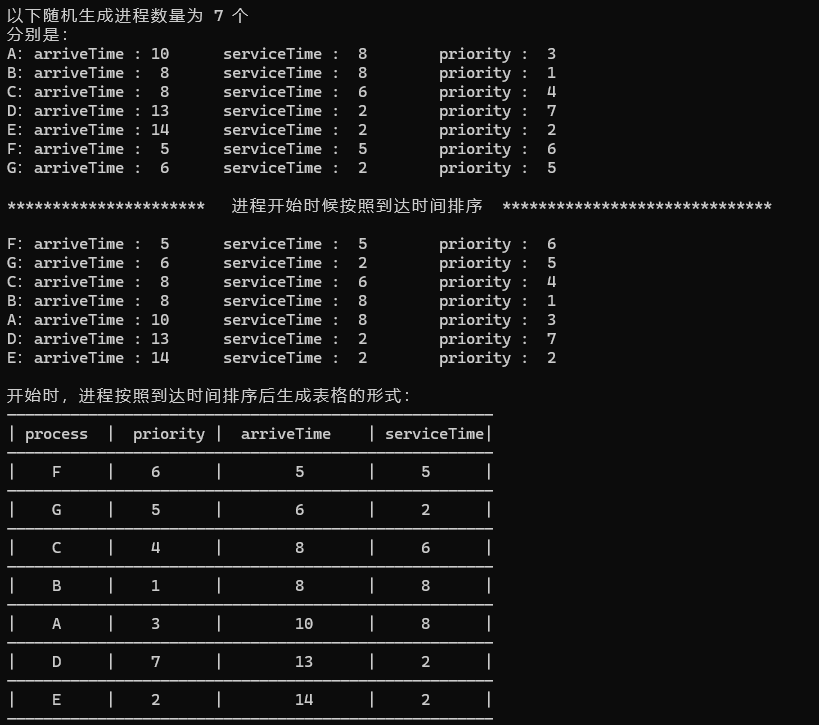
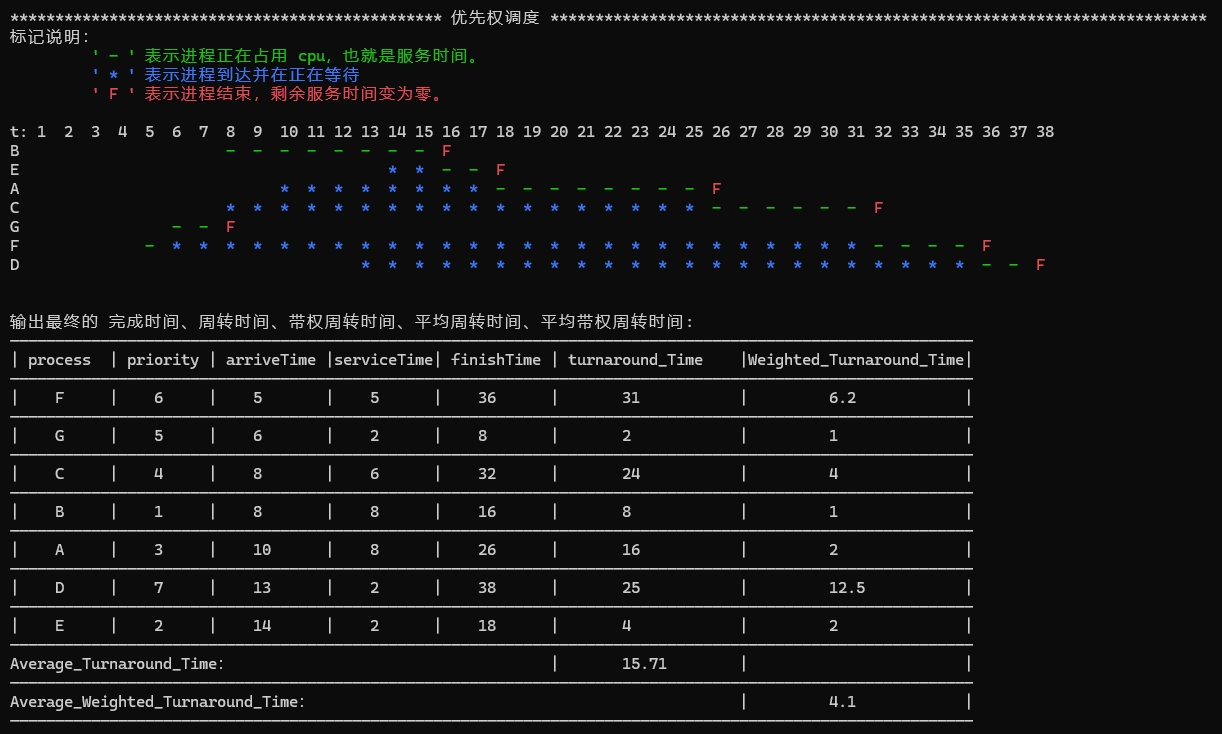
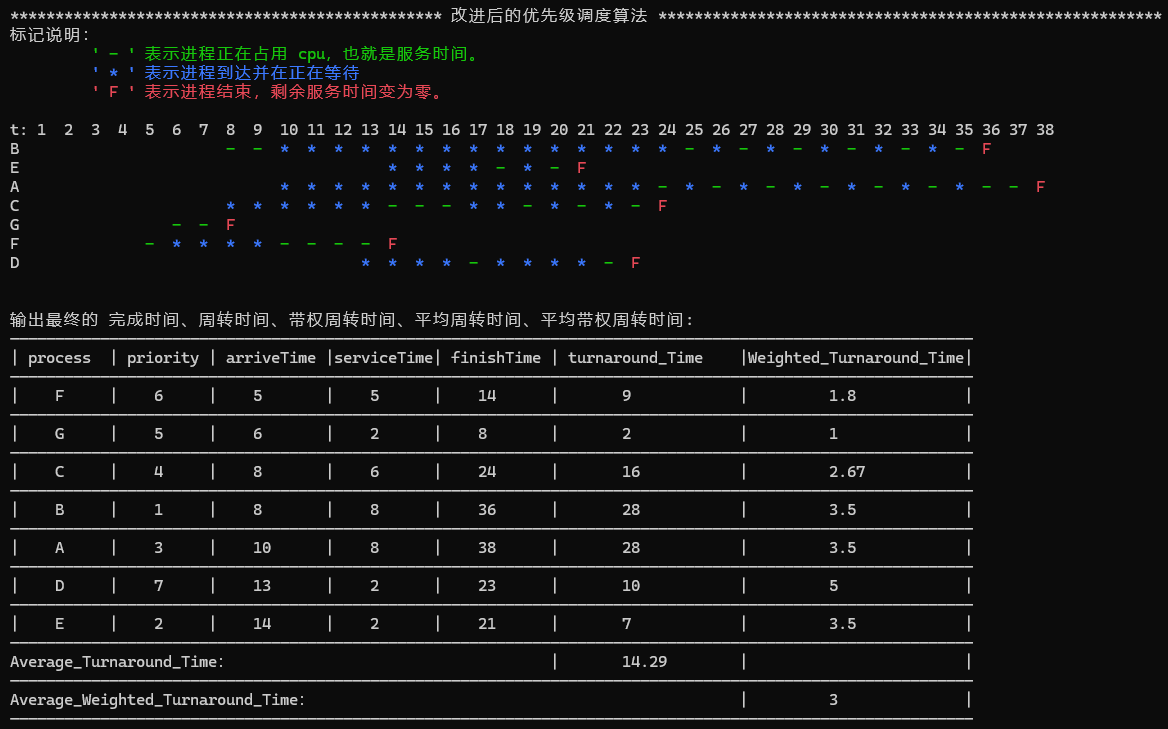
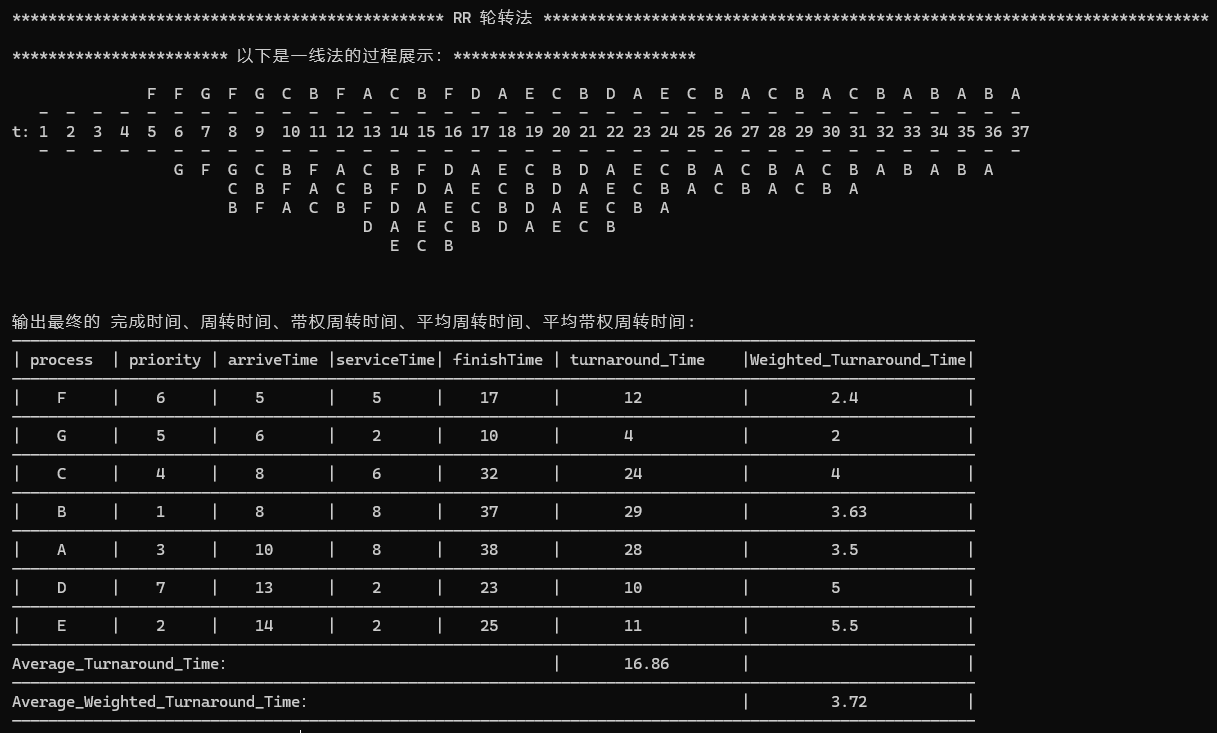
八、温馨说明

学力有限，拙文恐有未周，敬祈读者批评指正，由甚感激！若有讹误或排版不当，尚祈见谅！
☺️☺️☺️☺️☺️