操作系统:存储管理的具体分析实现
文章目录
一、操作目的
存储管理的主要功能之一是合理地分配空间。请求页式管理是一种常用的虚拟存储管理技术。本操作的目的是通过请求页式管理中页面置换算法模拟设计,了解虚拟存储技术的特点,掌握请求页式存储管理的页面置换算法。
二、操作内容
通过计算不同算法的命中率比较算法的优劣。同时也考虑了用户内存容量对命中率的影响。
命中率 = 1 - 缺页率
页面失效次数为每次访问相应指令时,该指令所对应的页不在内存中的次数。在本实验中,假定页面大小为 1k,用户虚存容量为 32k,用户内存容量为 2 页到 32 页。通过随机数产生一个指令序列,共 320 条指令。
A、 指令的地址按下述原则生成:
-
50%的指令是顺序执行的
-
25%的指令是均匀分布在前地址部分
-
25%的指令是均匀分布在后地址部分
B、具体的实施方法是:
-
在[0,319]的指令地址之间随机选取一起点 m;
-
顺序执行一条指令,即执行地址为 m+1 的指令;
-
在前地址[0,m+1]中随机选取一条指令并执行,该指令的地址为 m’;
-
顺序执行一条指令,地址为m’+1的指令在后地址[m’+2,319]中随机选取一条指令并执行;
-
重复上述步骤 1)~5),直到执行 320 次指令
C、 将指令序列变换称为页地址流
在用户虚存中,按每 k 存放 10 条指令排列虚存地址,即 320 条指令在虚存中的存放方式为:
第 0 条~第 9 条指令为第 0 页(对应虚存地址为[0,9]);
第 10 条~第 19 条指令为第 1 页(对应虚存地址为[10,19]);
. . . . . . . .
第 310 条~第 319 条指令为第 31 页(对应虚存地址为[310,319]);
按以上方式,用户指令可组成 32 页。
三、实现目标
1、实现FIFO、LRU、OPT 算法和 Clock 算法。
四、关键要求
1、计算相应算法的用户内存从 2k~32k 时的命中率;
2、比较各种算法的命中率;
3、分析当用户内存容量增加是对命中率的影响。
五、操作过程
1、算法逻辑:
1. FIFO(先进先出)算法
主要思想:FIFO 算法基于队列的思想,认为最先进入内存的页面也是最早可能不再需要的页面。
步骤:
维护一个队列,记录页面进入内存的顺序。
当需要替换页面时,选择队列中最先进入内存的页面进行替换。
使用一个队列来维护页面的进入顺序,并使用一个集合来快速判断页面是否在内存中。
2. LRU(最近最久未使用)算法
主要思想:LRU 算法基于最近使用的页面最可能被再次使用的假设。
步骤:
维护一个队列,记录页面的访问顺序。
每次访问一个页面时,将其移动到队列的末尾。
当需要替换页面时,选择队列中最久未被访问的页面进行替换。
3. OPT(最佳置换)算法
主要思想:OPT 算法基于未来访问的页面,选择未来最长时间不会被访问的页面进行替换。
步骤:
预处理阶段,记录每个页面的所有访问位置。
当需要替换页面时,查看当前内存中的页面,选择未来最长时间不会被访问的页面进行替换。
使用一个哈希表来存储每个页面的访问位置,以便快速查找。
4. CLOCK(时钟)算法
主要思想:CLOCK 算法是 FIFO 和 LRU 的折中,使用一个指针和一个标记位来模拟页面的使用情况。
步骤:
维护一个指针,指向内存中当前检查的页面。
每个页面有一个标记位,表示该页面是否被最近使用过。
当需要替换页面时,从指针位置开始,查找标记位为 false 的页面进行替换。
如果找到标记位为 true 的页面,将其标记为 false,并继续查找。
2、四种算法的流程图:
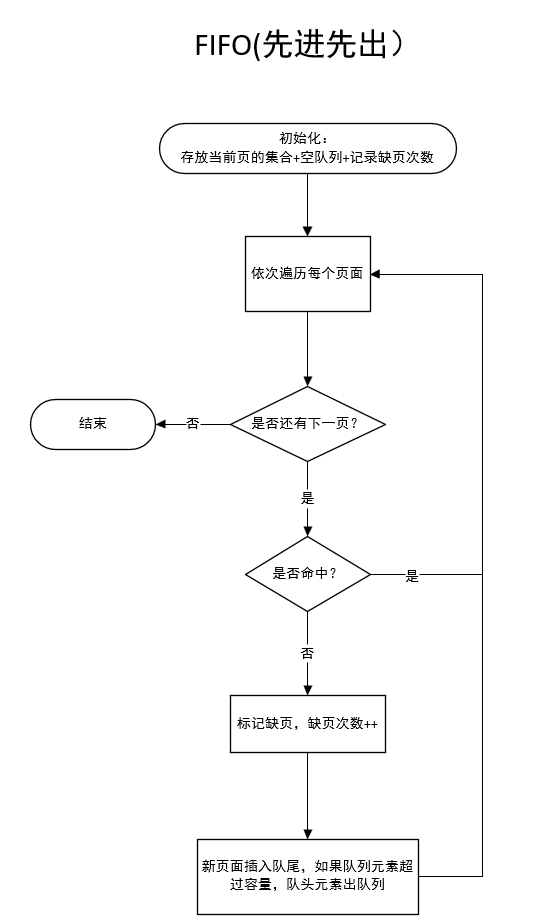
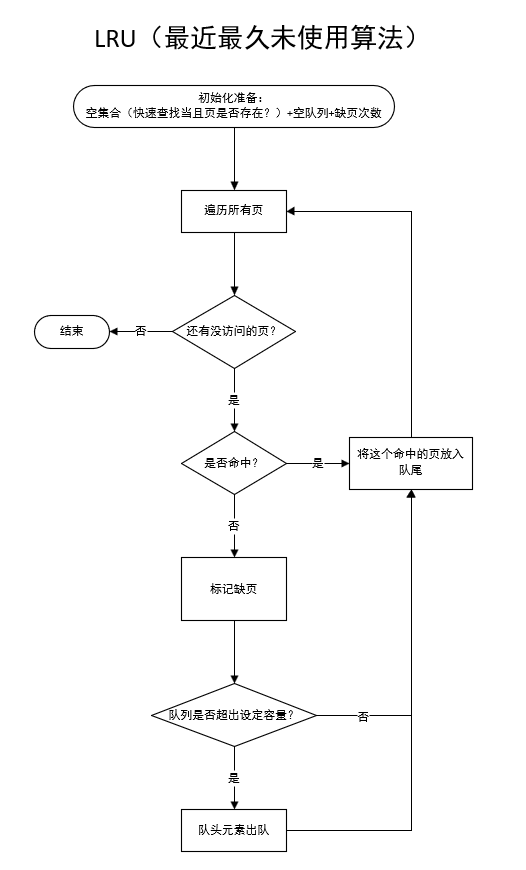
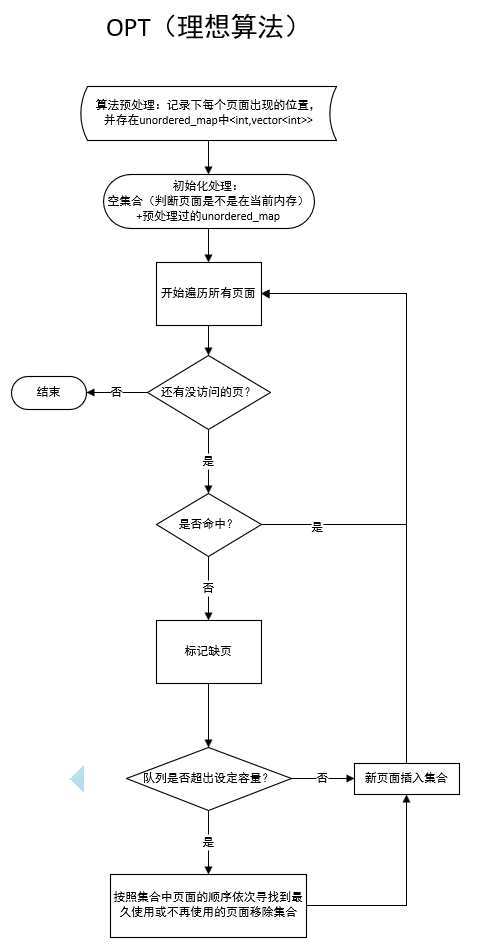
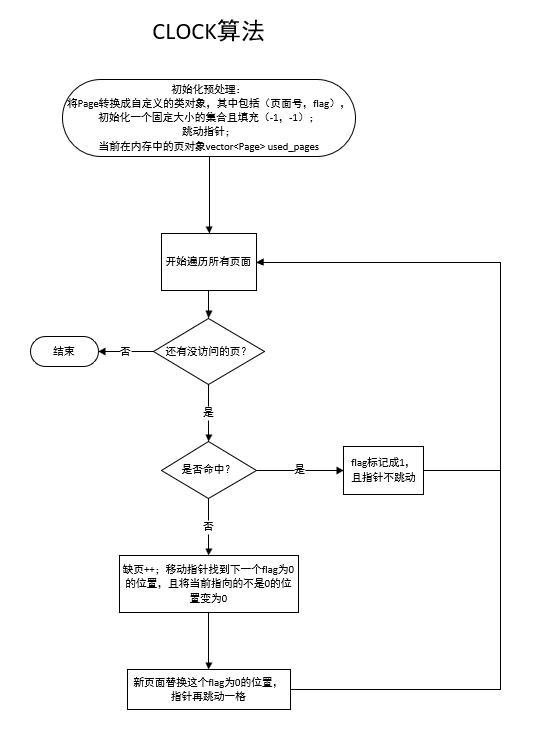
六、遇见问题
总体分为以下几个方面的问题:
- 随机数的生成问题
其实刚开始的随机数是用的rand(),但是对于这次实验的320个随机数并且也是考察重点之一,所以不能再用这种随机性比较差的随机数生成器,这个时候我们想到用C++11的随即库中的random_device + mt19937,保证了生成的随机数严格均匀,避免出现例如某个页面中的十个序号没有被生成的情况导致最后的32个内存页面的命中率高于90%的极端情况。
其次就是随机数生成的时候要保证符合区域的要求:25%,50%,25%的情况,所以我们要在每次使用随机数的时候去考虑生成的范围,避免发生m’+2越界的情况。
- 当前在内存中的页面查找问题
处理内存中是否存在当前遍历到的页面,因为刚开始对于FIFO和LUR算法都是基于队列的实现,实现起来页比较简单,但是队列无法遍历,所以只能将当前队列中的元素在放入一个新的可遍历的容器中。
这就需要考虑到效率的问题,刚开始用的是数组,那这就非常的低效,还需要考虑内存释放的问题。
其次考虑vector+find_if,但是还是不高效加上还要写仿函数,然后我就去查了资料,用了基于哈希表的unordered_set<int> ,避免了时间开销,何况是320个比较大的数据量。
下面我们具体比较一下三类容器对于查找的优劣:
| 容器选择 | 时间复杂度 | 适用性分析 |
|---|---|---|
| unordered_set | O(1) | 最优选择:快速判断页面是否在内存中,高频操作(命中检查、替换)效率最高。 |
| set | O(log n) | 关键的自动有序的性质浪费,而非顺序情况,红黑树开销十分的冗余。 |
| vector | O(n) | 连续内存适合遍历,但页面置换需频繁查找和修改,线性时间复杂度过高。 |
接着,在四种算法中,unordered_set<int> 的作用都是一样的,只用来查找当前页是否在内存块中,
| 算法 | 依赖的顺序 | 为何无需 set 的有序性? |
|---|---|---|
| FIFO | 页面进入内存的时间顺序 | 用 queue 维护顺序,unordered_set 仅负责快速命中检查。 |
| LRU | 页面最近访问的时间顺序 | 用 queue 维护顺序,unordered_set 仅存储页面是否存在。 |
| OPT | 页面未来访问的先后顺序 | 通过预处理的访问序列计算,unordered_set 仅存储当前页面。 |
| CLOCK | 环形扫描顺序(非页号) | 指针移动和标记位维护访问状态,unordered_set 仅用于快速确认页面是否在内存。 |
- OPT算法的具体问题
在OPT算法中,主要的时间消耗就是在查找当前页面下一次使用的时间,来确定该页面能不能被替换,那么这个时候,怎么高效的查找就是问题。
当然首先能想到的是每次判断内存块中的页面时候,我们就遍历一次后面的页面,来找到下一个位置,这样的方法必然是比较低效的。
其次我就想到了用map的key_value性质,只要我们将key的值设置成页面的页号,value的值我们用一个集合来表示,集合里面就是每次这个页号出现的位置,比如整个页面流的顺序是:1 2 2 3 4 2 5,那么对于2来说,就是map[2,(1,2,5)],代表2号页面在 1 2 5 号位置出现,那么只要将所有的页面在开始进行这样的处理,并存于map容器中,通过map的性质find快速查找到当前页面下一次出现的位置。
为了再优化程序,因为没有用到排序的性质,所以完全可以使用unordered_map通过哈希表就可以解决这个问题了。
- CLOCK算法的具体问题
对于CLOCK我原本想将元素和其是否访问标志(0/1)储存在一个容器中,使用 pair<int, bool>,但是在使用 unordered_set 时,pair 不能作为 key。
后面又想到用两个容器,一个页面容器,一个标记容器,但是要确定相关索引的时候复杂,代码的冗余性就高。
那么对于这样一个页面对象存在多个性质(号码,访问),最后我们还是选择用类来实现,使用一个类来表示页面和标记位,但是这样又会产生一个问题,那么查找的页面的时候又比较慢了,因为只能通过自己的函数来实现。暂时也没有想到更好的方法,这也是未解决的问题之一。
七、相关思考和说明
-
算法的正确性验证问题
因为没有要求写出算法的过程,只用写出每个算法对比的结果,那么怎么验证自己的程序是否是想要的过程实现的呢?
为此我对每个算法都写了一个过程化的实现,用已有数据中三个已有数据来验证是否是想要的过程,因为前面实现随机数的的页面序列是无需展现过程化,其实尝试过,出来的效果并不好,太多了数据就比较乱,所以前面320个随机数的算法实现就只用简化版的算法函数即可。
到了已有数据我们再用过程化的函数,以免造成不必要的代码和时间浪费。
-
为OPT算法进行说明:
我们知道如果当前有多个页面都在以后不会被访问到,那我们应该替换哪个?
在一些写法中,我们选择替换其中最近未使用的。但是在程序中,为了减少不必要的前序查找额外的时间开销,我们就直接按照当前unordered_set的顺序,找到第一个永远不会使用的页码替换,减少查找时间的开销!
八、附录
1、核心代码
// FIFO 算法————先进先出
void FIFO_Process(const vector<int>& page_stream, int capacity, string** arr) {
unordered_set<int> present; // 当前在内存中的页
queue<int> FIFO_queue;
int miss = 0;
int i = 0;
for (int page : page_stream) {
arr[0][i] = to_string(page); // 将页号存入数组
if (present.count(page)) {
++i;
continue;
}
miss++;
arr[1][i] = "Y"; // 表示缺页
if (present.size() < capacity) { // 用户内存容量还有空位
present.insert(page);
FIFO_queue.push(page);
}
else {
int removed = FIFO_queue.front();
FIFO_queue.pop();
arr[capacity + 2][i] = to_string(removed); // 将替换的页面存入数组
present.erase(removed);
FIFO_queue.push(page);
present.insert(page);
}
QueueToArray(FIFO_queue, arr, capacity + 2, i); // 将队列拷贝到二维数组中
++i;
}
}
// LRU 算法
void LRU_Process(const vector<int>& page_stream, int capacity, string** arr) {
unordered_set<int> present; // 当前在内存中的页
queue<int> LRU_queue;
int miss = 0;
int i = 0; // 页号
for (int page : page_stream) {
arr[0][i] = to_string(page); // 将页号存入数组
if (present.count(page)) {
// 命中需要调整队列中的位置,因为是最近使用的应该放到队尾
queue<int> temp_queue;
while (!LRU_queue.empty()) {
int front_page = LRU_queue.front();
LRU_queue.pop();
if (front_page != page) {
temp_queue.push(front_page);
}
}
LRU_queue = temp_queue; // 更新队列
LRU_queue.push(page); // 将命中的页放入队尾
}
else {
miss++; // 没有命中,缺页的情况
arr[1][i] = "Y"; // 表示缺页
if (present.size() < capacity) { // 用户内存还有空位
present.insert(page);
LRU_queue.push(page);
}
else { // 没有空位,需要进行页面置换,因为前面已经处理过队列了,所以这里替换的一定是队头页面
int removed = LRU_queue.front();
LRU_queue.pop();
arr[capacity + 2][i] = to_string(removed); // 将替换的页面存入数组
present.erase(removed);
LRU_queue.push(page);
present.insert(page);
}
}
QueueToArray(LRU_queue, arr, capacity + 2, i); // 将队列拷贝到二维数组中
++i;
}
}
// OPT 理想算法
void OPT_Process(const vector<int>& page_stream, int capacity, const unordered_map<int, vector<int>>& Page_pos, string** arr) {
unordered_set<int> present;
int miss = 0;
for (int i = 0; i < page_stream.size(); ++i) {
int page = page_stream[i];
arr[0][i] = to_string(page);
if (present.count(page)) continue; // 命中
miss++;
arr[1][i] = "Y"; // 表示缺页
if (present.size() < capacity) { // 用户内存还有空位
present.insert(page);
}
else {
// 寻找最远使用的页
int farthest = -1, replace_page = -1;
for (auto p : present) {
int next = find_next(p, i, Page_pos);
if (next == INT_MAX) { // 先找永久不会再使用的页
replace_page = p;
break;
}
if (next > farthest) { // 再找最远使用的页
farthest = next;
replace_page = p;
}
}
arr[capacity + 2][i] = to_string(replace_page); // 将替换的页面存入数组
present.erase(replace_page);
present.insert(page);
/*
所以当内存中有多个页面后面都不在被用到,那么该逻辑替换的应该是 unordered_set<int> present 顺序来替换
*/
}
// 将当前内存中的页存入二维数组
int j = 2;
for (auto p : present) {
arr[j][i] = to_string(p);
j++;
}
}
}
// Clock 算法
void CLOCK_Process(const vector<int>& page_stream, int capacity, string** arr) {
// 把 page_stream 中的页号转换为 Page 类对象
vector<Page> pages; // 用于遍历的页对象容器
for (auto it = page_stream.begin();it != page_stream.end();++it) {
Page p(*it);
pages.push_back(p);
}
Page page_temp(-1); // 用于初始化的页对象
vector<Page> used_pages; // 用于存储当前在内存中的页对象
used_pages.resize(capacity, page_temp); // 初始化内存页对象
int miss = 0;
int p = 0; // 跳动指针
for (int i = 0;i < page_stream.size();++i) {
arr[0][i] = to_string(pages[i].page_num); // 将页号存入数组
// 判断当前页是否在内存中
int pos = find_page(used_pages, pages[i]);
int replace_page = -1;
if (pos != -1) {
used_pages[pos].page_flag = true; // 如果在内存中,设置标记位为 true // 指针不跳动
}
else {
// 否则说明不在页面中,那就发生缺页
miss++;
arr[1][i] = "Y"; // 表示缺页
// 先判断指针指向的是否是falg为 false 的页
while (used_pages[p].page_flag) {
// 如果是 true,记录为 false,跳到下一个页面
used_pages[p].page_flag = false; // 设置为 false
p = (p + 1) % capacity; // 跳动指针且以免越界
}
replace_page = used_pages[p].page_num; // 记录替换的页面
if (replace_page != -1) arr[capacity + 2][i] = to_string(replace_page); // 将替换的页面存入数组
used_pages[p] = pages[i]; // 将当前页放入内存
p = (p + 1) % capacity; // 跳动指针且以免越界
}
// 将当前内存中的页存入二维数组
int j = 2;
for (auto p : used_pages) {
if (p.page_num != -1) {
arr[j][i] = to_string(p.page_num);
}
j++;
}
}
}
2、结果显示:
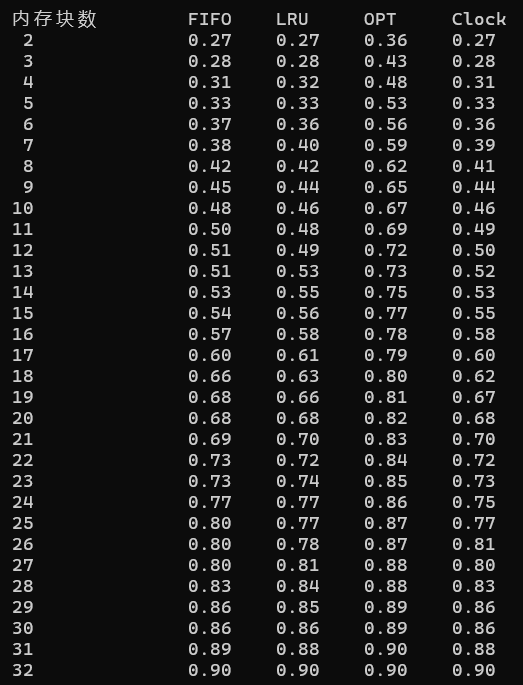

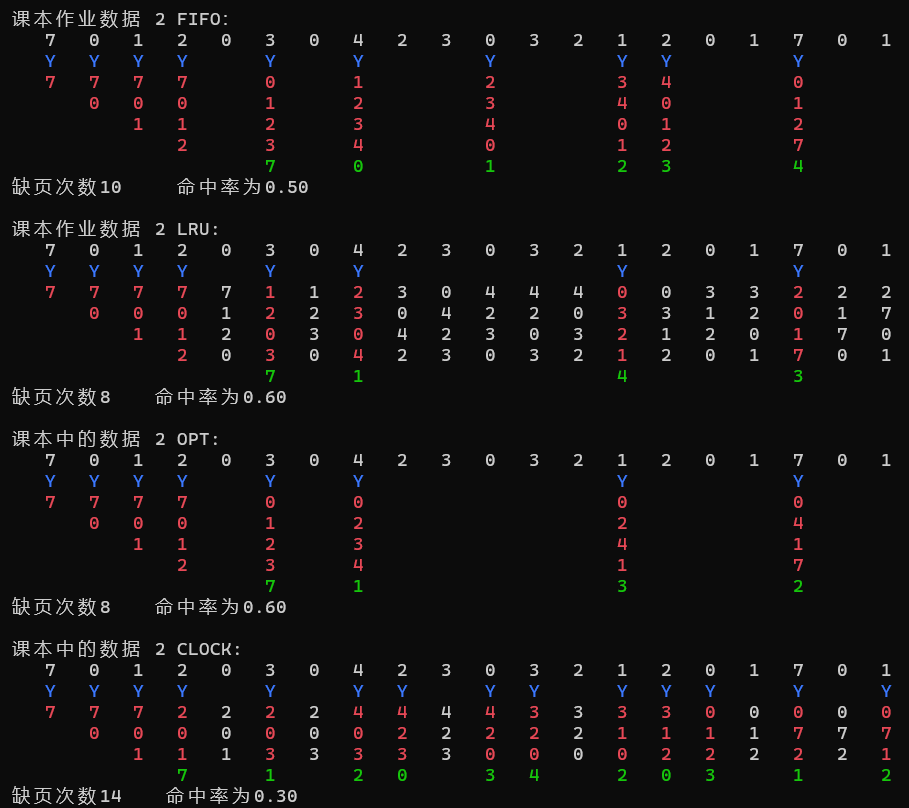

3、四种方法的比较:
| 算法 | 优势 | 不足 | 命中率 |
|---|---|---|---|
| FIFO | 实现简单,只需维护队列,低开销(O(1) | 无法反映访问局部性(缺页率随容量增加而升高) | 较低(尤其是访问模式不符合先进先出规律时) |
| LRU | 通过过去预测未来,实现简单,队列形式 | 可能出现刚出队的页面又请求访问的情况(例如数据三),导致缺页率高 | 较高(优于 FIFO) |
| OPT | 理论最优缺页率(预知未来访问序列) | 用于理论分析,实际情况知道预测未来,且需要体现提取出所有页面出现的位置 | 最高,理想算法(所有算法的下界) |
| CLOCK | 近似 LRU,但开销可能更低,通过软件的方式去解决硬件的问题 | 实现稍微复杂(环形扫描+标记,通过类对象的实现) | 较高(优于 FIFO) |
九、温馨说明
学力有限,拙文恐有未周,敬祈读者批评指正,由甚感激!若有讹误或排版不当,尚祈见谅!

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








