回溯算法之子集问题

回溯算法之子集问题

一、回溯算法简介

回溯算法是一种穷举算法，因此回溯算法是一种暴力求解的算法，它的时间复杂度可以达到O(N!)，但是有些问题我们通过暴力枚举的方式来求解显得更简单，比如经典的子集问题和排列问题

二、回溯算法与树的遍历

其实回溯算法本质上就是在遍历一棵树，这棵树和我们常见的二叉树不同，这棵树可以是多叉的，一般来说解决回溯问题可以分为两个步骤进行：
（1）构造回溯树结构，回溯算法本质上就是在对这棵回溯树进行先序遍历
（2）编写树的递归版本的先序遍历

三、子集问题

3.1 子集问题简介

子集问题就是求一个集合的所有子集，注意集合的元素是不能重复的，并且空集是任何一个集合的子集

3.2 子集问题的回溯树

子集问题的回溯树可以有两种构建方式：
（1）构建成一棵二叉树形式
（2）构造成一棵普通树形式
具体的例子如下图所示，上边是二叉树形式的子集树，下边是普通树形式的子集树

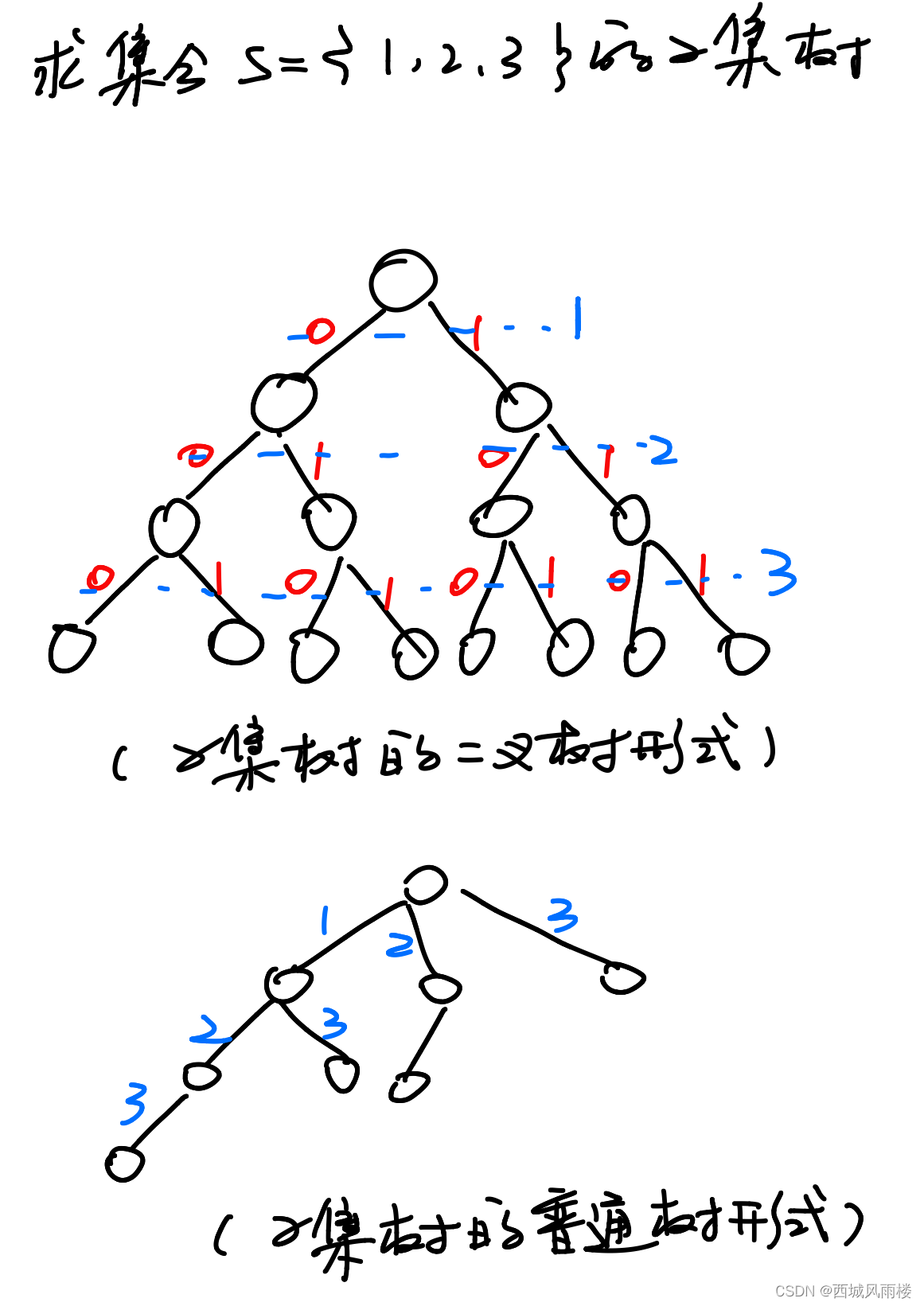
3.2.1 二叉树形式结构解释

将结点看作是函数递归栈中的一个栈帧，而边代表我们在当前栈帧中做出的选择，左孩子边表示我们在当前栈帧中选择第i个元素（这里假设当前栈帧的深度是i，事实上通过观察我们也可以得出，栈的深度最多是4），右孩子边表示我们在当前栈帧中不选择第i个元素，依次类推，因为这是一棵二叉树，因此我们可以很容易写出如下的伪代码

void back_trace(int[] nums, int i) {
	if (i >= nums.length) {
		printf(records);
		return;
	}
	// records表示当前集合
	// 表示向集合中添加nums[i] 
	records[i] = true;
	// 相当于遍历二叉树的左子树
	back_trace(nums, i + 1);
	// 表示不向集合中添加nums[i]
	// 因为我们的递归树中默认遍历二叉树的右子树是不添加操作
	records[i] = false;
	// 相当于遍历二叉树的左子树
	back_trace(nums, i + 1);
} 

3.2.2 普通树形式结构解释

依然是将结点看作是栈帧，同一层的结点表示在同一个递归栈中，结点的分支表示当前选择的是第几个元素，第零层（根节点）表示我们当前子集的第一个元素可以选择的有{1, 2, 3}，第二层的第一个结点的边表示我们在选择了1的情况下，还可以选择哪些元素，这里是{2, 3}，依次类推
因为这是一个普通的树，所以我们对普通树的先序遍历需要借助for循环来完成，伪代码如下：

void back_trace(int[] nums, int i) {
	// 之所以在这里进行打印，是因为先序遍历树的过程中
	// 每经过一段路径就会产生一个新的集合，这从图中
	// 也可以很容易看出来
	printf(records);
	if (i >= nums.length) {
		printf(records);
		return;	
	}	
	// 通过for循环，依次访问同一层的其他结点
	for (int j = i; j < nums.length; j++) {
		// 将第i层的第j个元素添加进子集中
		records[i] = true;
		back_trace(nums, j + 1);
		// 因为records是共享的，所以当第j个结点处理完毕之后
		// 应该将第j个结点产生的数据清除，否则会影响其他结点
		records[i] = false;		
	}
}

四、子集问题具体代码实现

/**
 * 使用回溯算法解决子集问题
 *
 * @author 西城风雨楼
 */
class Solution {
    /**
     * 使用回溯算法求解子集问题
     *
     * @param nums 一组数列
     * @return 返回所有的子集
     */
    public List<List<Integer>> subsets(int[] nums) {
        List<List<Integer>> res = new ArrayList<>();
        backTrace2(nums, 0, res, new ArrayList<>());
        return res;
    }

    public void backTrace1(int[] nums,
                          int startIndex,
                          List<List<Integer>> res,
                          List<Integer> curSubSet) {
        res.add(new ArrayList<>(curSubSet));
        if (startIndex >= nums.length) {
            return;
        }
        for (int i = startIndex; i < nums.length; i++) {
            curSubSet.add(nums[i]);
            backTrace1(nums, i + 1, res, curSubSet);
            curSubSet.remove(curSubSet.size() - 1);
        }
    }

    public void backTrace2(int[] nums,
                           int startIndex,
                           List<List<Integer>> res,
                           List<Integer> curSubSet) {
        if (startIndex >= nums.length) {
            res.add(new ArrayList<>(curSubSet));
            return;
        }

        curSubSet.add(nums[startIndex]);
        backTrace2(nums, startIndex + 1, res, curSubSet);
        curSubSet.remove(curSubSet.size() - 1);
        backTrace2(nums, startIndex + 1, res, curSubSet);
    }

    public static void main(String[] args) {
        int[] nums = {1, 2, 3};
        System.out.println(new Solution().subsets(nums));
    }
}