跳表

结论

跳表是一个二维的链表，通过牺牲一部分空间来换取比链表更快的速度。

从链表开始

链表在查找数据的时候，我们需要从头往后进行遍历，时间复杂度为O(n)，如果我们为了提高链表在查找时候的效率引入了跳表的结构，就是构建了一个二维的链表。

我们通过将提取一条有序的链表上的若干个节点，在其之上构建出了一层新的链表，通过先检索上层的链表来一步步的缩小范围，直到最后确定位置。

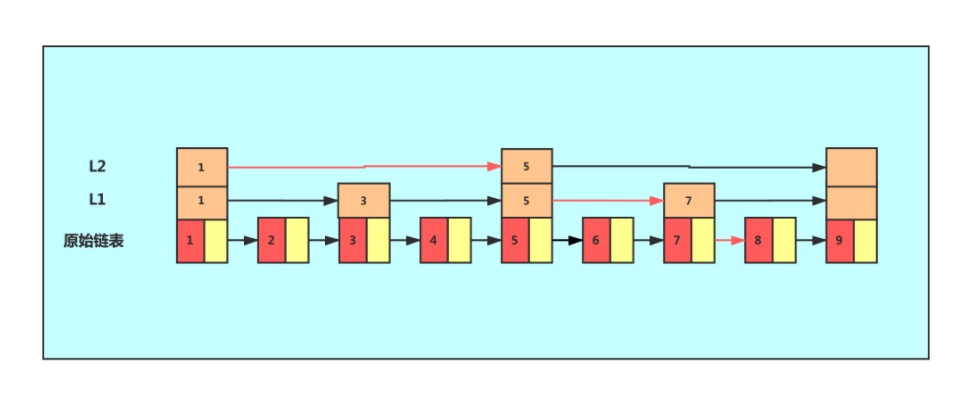
跳表的遍历

拿上图举例， 假设我们需要找到数据 8，那么遍历的步骤如下

1. 从L2的第一个节点出发，找到该条链表中小于等于数据8的最大值，也就是5.
2. 那么在找到5之后，往下走，就到了下面一层 L1，在L1层也是重复步骤1.
3. 在L1层，通过重复步骤1，我们找到了节点 7，继续往下走，到了原始链接层，
4. 继续重复步骤1，就找到了数据8

跳表的查找效率

如果一个链表有n个节点，每两个节点之间抽取出来一个作为索引的话，那么第一层索引就是n/2个，第2层索引就是n/4个，那么第m层的节点数就是n/(2^m)。
假设m层是最上面那层的话，也就是说m层只有两个节点，n/(2^m) =2 ，那么m=$log(n)-1$，我们每层要查询k个节点的话，也就是 $O(k\ast log(n))$
跳表就是一个典型的采用时间换空间的数据结构

跳表的插入(难点)

方法1:跳表的插入不是单纯的遍历底层链表，然后插入一个节点这么简单，当插入一个节点之后，需要考虑要将上层的链表也要进行更新，但是不是每一次都要进行更新的，因此就需要一个随机数

注意这里的随机数不能每次都新生成一个Random对象，那样的话，每次得到的随机数都要一样的。

方法2:这里我们采用一个更新上层节点的时候，可以采用一个逆向的思路，首先，先从最上面的一层的首节点开始，进行遍历，在最下面那层找到能够插入的位置，进行数据的插入，之后我们生成一个随机数，如果大于阈值，就复制最下面一层，将复制的那层作为最底下的那层。如果小于阈值，那就不进行复制。

插入流程(默认，除第一层外，每一层都要进行插入)

在上面的跳表中插入数据 6的流程如下

1. 从最上层的1开始，由于下一个节点大于6，那么节点1就是不大于插入数据的最大的节点，进入下一层
2. 第二层的下一个节点是7，我们要根据随机数去判读是否要插入节点，节点被插入
   
3. 那么节点1继续往下走到下一层，遍历节点发现节点，要被插入到4于7之间(这里)，继续插入节点
   
4. 从节点4往下走，到了下一层，也就是原始层，遍历节点，发现应该在节点5到7之间进行节点插入
   

跳表的删除

删除与查询基本相似，唯一不同的是，在找到节点之后，将当前层级的节点删除的同时，下层的节点也要删除。

redis在底层中，使用了跳表，为什么不是使用B树或者B+树

1. 首先这几种数据结构在检索上的复杂度都是基本差不多的。
2. B树由于单个节点存储多个数据，redis使用B树的话，就需要很多内容，MySQL是由于某个数据被检索到，其附近的数据也有很大可能被再次查询。
3. 跳表对于范围查询 更好一些，同时更加简单
4. 在插入节点的话，B树会引发子树的调整