参考:
维基百科
算法研究之贝塞尔曲线
贝塞尔曲线(The Bézier Curves),是一种在计算机图形学中相当重要的参数曲线(2D,3D的称为曲面)。
贝塞尔曲线于1962年,由法国工程师皮埃尔·贝塞尔(Pierre Bézier)所发表,他运用贝塞尔曲线来为汽车的主体进行设计。

一阶贝塞尔曲线
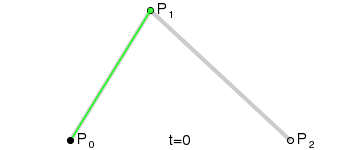
给定点P0、P1,线性贝塞尔曲线只是一条两点之间的直线。这条线由下公式给出:
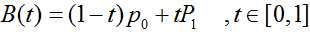
当参数t变化时,其变化过程如下
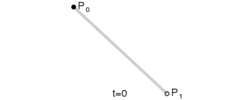
线性贝塞尔曲线函数中的t会经过由P0至P1的B(t)所描述的曲线。例如当t=0.25时,B(t)即一条由点P0至P1路径的四分之一处。就像由0至1的连续t,B(t)描述一条由P0至P1的直线。
二阶贝塞尔曲线
二阶贝塞尔曲线(抛物线) 路径由给定点P0、P1、P2的函数B(t)追踪:
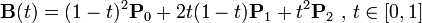
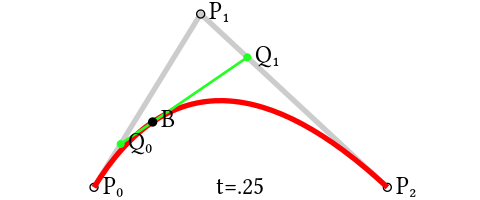
为建构二次贝塞尔曲线,可以以中介点Q0和Q1作为由0至1的t:
- 由P0至P1的连续点Q0,描述一条线性贝塞尔曲线。
- 由P1至P2的连续点Q1,描述一条线性贝塞尔曲线。
- 由Q0至Q1的连续点B(t),描述一条二次贝塞尔曲线。
三阶贝塞尔曲线
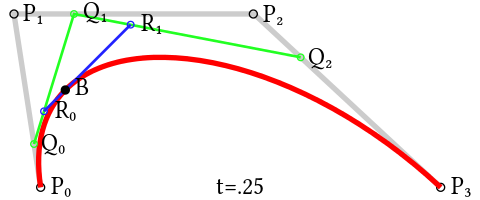
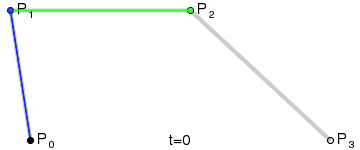
为建构高阶曲线,便需要相应更多的中介点。对于三次曲线,可由线性贝塞尔曲线描述的中介点Q0、Q1、Q2,和由二次曲线描述的点R0、R1所建构:
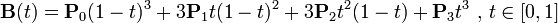
高阶曲线公式
更高阶的贝塞尔曲线,可以用以下公式表示:
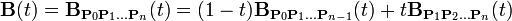
在编程中实现
计算机绘图中,要“画”出贝塞尔曲线,一般需要进行较多的计算,然后绘制出来,类似这样:
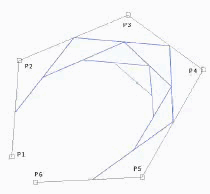








 本文介绍了由法国工程师皮埃尔·贝塞尔于1962年提出的贝塞尔曲线的概念及其在计算机图形学中的应用。文章详细解释了一阶、二阶及三阶贝塞尔曲线,并通过数学公式展示了如何构建这些曲线。
本文介绍了由法国工程师皮埃尔·贝塞尔于1962年提出的贝塞尔曲线的概念及其在计算机图形学中的应用。文章详细解释了一阶、二阶及三阶贝塞尔曲线,并通过数学公式展示了如何构建这些曲线。

















 752
752

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










