欧拉公式

最新推荐文章于 2025-08-09 17:33:05 发布
原创 最新推荐文章于 2025-08-09 17:33:05 发布 · 3.2k 阅读 · 4 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

e^{\pi i} = -1

本文围绕以下视频进行说明：

https://www.youtube.com/watch?v=mvmuCPvRoWQ

https://www.youtube.com/watch?v=F_0yfvm0UoU

一个数字同时代表三样事物

1. 一条无限长数轴上的一个点

2. 将数轴向自身方向活动的动作（数字x 可以看做一个加子，x是正数对应将整个数轴向右移动 \left | x \right | 个单位，x是负数对应将数轴向左 \left | x \right | 个单位）

3. 将数轴伸展或压缩的动作（称之为乘子）

e的x次方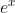（e^{x}）的含义

e^{x}这一运算（更确切的说应该是幂函数这一运算）的目的是把加子转换为乘子 e^{x} 满足f(x+y) = f(x)f(y)这一性质，我们不应该将e^{x}理解为x个e相乘，因为在x为负数，分数，无理数，虚数的时候这是无法理解的，而是理解为 输入为 滑动数轴的动作，输出为 伸展或压缩数轴的动作，的一种函数对应关系，即f(x+y)= f(x)f(y)这一性质本身定义了幂函数运算。

e^{x}这个“自然”函数是由f(x+y)=f(x)f(y)所定义的 而不是x个e相乘所定义的

e的x次方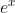（e^{x}）的含义(复数)

视频中利用类比法，直接给出了其意义，

1. x为实数时e^{x}代表输入为数轴(实轴)的滑动，输出为数轴(实轴和虚轴同时)伸展或压缩；

2. x为纯虚数时代表输入为 虚轴的滑动，输出为实轴和虚轴的旋转；

3. x为复数时代表输入为实轴和虚轴的滑动，输出为实轴和虚轴的伸缩加旋转

推理结果

e^{\pi i}  x为纯虚数，输入是在虚轴滑动\pi个单位，所以是将数轴旋转\pi个弧度，等价于将复数对应的向量旋转\pi个弧度，方向正向（逆时针），也就对应-1

e^{\theta i} 等价于将复数向量旋转 \theta 个弧度，所以等价于表达式cos\theta + i sin\theta 即  欧拉公式 e^{\theta i} = cos\theta + i sin\theta

视频里并没有介绍关键的部分：

1.e^{\theta i} 输入为虚轴向上滑动 \theta个单位，为什么正好对应输出是复数向量旋转 \theta个弧度，2^{\theta i}对应旋转多少弧度？

2.为什么e的幂次为虚数时，输出为旋转动作，视频结尾中提到了如何把e^{x}看做复平面上的变换，但我没看懂。

 

自己的理解

在复变函数中，求解析函数的导函数，可以使用柯西黎曼方程，但指数函数这种初等函数，可以直接套用微积分中的求导公式，所以

可以看到e^z 和 e^x(cosy+isiny)这两个函数的导数都等于它们自身，和指数函数的性质一致。其实不仅求导的的性质一致，加减乘除的性质也和指数函数一致。

所以我个人理解e^z只是e^x(cosy+isiny)一种表示形式的简化而已。这要看我们在复数域范围内是如何给出指数函数定义的，我们给出的定义可以根据三角函数来定义的：

expz = e^x(cosy + isiny)

其中expz可以用e^z来表示，e^z只是一个记号，它的实质是e^x(cosy + isiny)

如果我们将e^z做泰勒展开，会发现它们也是正好契合的。

 

高数往事(2) 欧拉公式的理解和证明。
duoyasong5907的博客
10-06 1268
如何理解简洁的欧拉公式？
什么是欧拉公式
back_room的博客
06-26 8581
欧拉公式在不同的学科中有着不同的含义。复变函数中，e^(ix)=(cos x+isin x)称为欧拉公式，e是自然对数的底，i是虚数单位。拓扑学中，在任何一个规则球面地图上，用 R记区域个数 ，V记顶点个数 ，E记边界个数 ，则 R+ V- E= 2，这就是欧拉定理 ，它于1640年由笛卡尔首先给出证明，后来欧拉于 1752年又独立地给出证明，我们称其为欧拉定理，在国外也有人称其为笛卡尔定理。他被称为世界上最简洁的公式。
显式欧拉方法
05-31
显式欧拉方法，计算机专业课件，可直接运行
欧拉公式的意义
最新发布
创新改变世界！
08-09 1709
欧拉公式（Euler’s Formula）是数学中最重要的公式之一，它将。
如何通俗地解释欧拉公式1
08-03
根据给定的信息，本文将详细解释欧拉公式及其背后的数学概念。欧拉公式是一个非常重要的数学公式，它连接了指数函数、三角函数以及复数。接下来我们将深入探讨该公式的意义和背后的概念。 ### 一、复数基础 #### ...
matlab 数学实验 实验报告 欧拉公式 ROSSLER微分方程.docx
07-14
改进的欧拉公式，也称为中点法则，是在每个步长的中间点计算导数，公式为\( y_{n+1} = y_n + h \cdot f(x_n + \frac{h}{2}, y_n + \frac{h}{2}) \)，这种方法通常比向前欧拉公式更精确。 **ROSSLER微分方程**是一组...
欧拉公式求圆周率的matlab代码-Calculate-Pi:计算Pi
05-23
欧拉公式求长期率的matlab代码计算π 挑战的目的是练习将列表理解与输入和输出一起使用。 编写并提交一个Python程序，该程序通过计算以下总和来计算π的近似值： 当n接近∞时，该和接近π的真实值。 该方程式中的大...
欧拉公式求圆周率的matlab代码-Euler-Spiral:进行初始和最终位置+定向。使用以下公式返回欧拉螺旋参数k，伽玛和曲线长度：曲率K
05-23
欧拉公式求长期率的matlab代码欧拉螺旋 来源：形状完成的欧拉螺旋线本杰明·基米亚，伊拉娜·弗兰克尔和安娜·玛丽亚·波普斯库工程学院，布朗大学，普罗维登斯，R1 02912，美国 进行初始和最终位置+定向。 使用以下...
欧拉公式求圆周率的matlab代码-programming-differential-equations:使用Python进行微分方程编程的示
05-23
欧拉公式求长期率的matlab代码编程微分方程 一个存储库，存储Udacity课程中的工作：微分方程在实践中，以及使用Python进行科学编程入门中的示例。 涵盖了以下数值方法： 前向欧拉法 亨氏法 后向欧拉法 梯形法则 对于...
【二】欧拉公式
热门推荐
mrdonghe的博客
05-14 1万+
世界上最伟大的十个公式： 欧拉公式、麦克斯韦方程组、牛顿第二定律、勾股定理、薛定谔方程、质能方程、德布罗意方程组、1+1=2、傅立叶变换、圆的周长公式。 欧拉公式的巧妙之处在于，它没有任何多余的内容，将数学中最基本的e、i、π放在了同一个式子中，同时加入了数学也是哲学中最重要的0和1，再以简单的加号相连。高斯曾经说：“一个人第一次看到这个公式而不感到它的魅力，他不可能成为数学家。” 虽然不敢肯...
向前欧拉公式例题_简单实用！小学语文阅读理解答题万能公式，超全整理
weixin_39958559的博客
01-06 208
阅读理解一直是语文考试中失分的重灾区，面对试卷上的阅读理解题，理解文章意思的同时，在答题技巧上面也应下点功夫。 学习哥分享这份阅读理解中会用到的小技巧和不同题型的答题模式，希望对孩子有所帮助，一起来看看吧！01词语一、某句话中某个词换成另一个行吗？为什么？动词：不行。因为该词准确生动具体地写出了……形容词：不行。因为该词生动形象地描写了……副词：如(如：都，大都，非常只有等)：不行。因为该词准确地...
欧拉公式的三元
06-13
<think>我们首先需要理解用户的问题：用户想要了解欧拉公式在三元情况下的应用或表达形式。欧拉公式通常指的是复分析中的欧拉公式：$e^{ix}=\cosx+i\sinx$，这是二元形式（涉及实部和虚部）。而“三元形式”可能指欧拉公式在三维空间中的推广，例如在四元数或向量分析中的形式，或者是在三元数（如果存在）中的形式。但需要注意的是，三元数并不像四元数那样被广泛使用，因为三元数在乘法运算上存在缺陷（不可除），因此欧拉公式在三元数上的直接推广并不常见。然而，在数学和物理学中，欧拉公式可以推广到四元数。四元数是一种扩展复数的数学结构，包含一个实部和三个虚部。四元数的欧拉公式形式为：$$e^{\mathbf{u}\theta}=\cos\theta+\mathbf{u}\sin\theta$$其中$\mathbf{u}$是一个单位纯四元数（即实部为0，且三个虚部满足$u_x^2+u_y^2+u_z^2=1$），$\theta$是一个实数。另外，在三维空间中，旋转可以用四元数表示，而欧拉公式在四元数中用于描述旋转。这是欧拉公式在三维空间中的一个重要应用。因此，我们可能需要搜索以下内容：-欧拉公式在四元数中的形式（因为四元数有三个虚部，所以有时被称作三元形式？但严格来说四元数有四个分量）-三维空间中的旋转公式（欧拉-罗德里格斯公式）与欧拉公式的关系-是否存在三元数的欧拉公式？（但三元数不常用，可能没有标准形式）经过搜索，我们可能会发现以下信息：1.四元数的欧拉公式：对于单位四元数，我们可以用指数形式表示旋转。2.欧拉公式在三维旋转中的应用：通过四元数，我们可以将三维旋转表示为指数映射。因此，我们回答的重点应该是四元数形式的欧拉公式及其在三维旋转中的应用。我们进行网络搜索（模拟）后，整合信息如下：回答结构：-首先介绍四元数形式的欧拉公式。-然后说明其在三维旋转中的应用。-最后可以提及与经典欧拉公式的联系。注意：由于要求避免步骤词汇，我们使用换行来分隔不同的部分。同时，我们需要注意数学公式的格式要求。下面开始组织答案：欧拉公式在三维空间中的推广通常通过四元数实现。四元数是复数的扩展，包含一个实部和三个虚部，一般形式为$q=a+b\mathbf{i}+c\mathbf{j}+d\mathbf{k}$，其中$\mathbf{i},\mathbf{j},\mathbf{k}$是四元数的基本单位，满足$\mathbf{i}^2=\mathbf{j}^2=\mathbf{k}^2=\mathbf{i}\mathbf{j}\mathbf{k}=-1$。对于单位纯四元数（即实部为0且模长为1），记为$\mathbf{u}=u_x\mathbf{i}+u_y\mathbf{j}+u_z\mathbf{k}$，其中$u_x^2+u_y^2+u_z^2=1$，则指数形式$e^{\mathbf{u}\theta}$（$\theta$为实数）可以用欧拉公式推广形式表示：$$e^{\mathbf{u}\theta}=\cos\theta+\mathbf{u}\sin\theta$$该公式在三维旋转中具有重要应用。三维空间中的一个旋转可以通过一个单位四元数表示：$$\mathbf{q}=\cos\frac{\theta}{2}+\mathbf{u}\sin\frac{\theta}{2}$$其中$\mathbf{u}$是旋转轴方向的单位向量，$\theta$是旋转角度。使用该四元数旋转一个三维向量$\mathbf{v}$（表示为纯四元数）的公式为：$$\mathbf{v}'=\mathbf{q}\mathbf{v}\mathbf{q}^{-1}$$由于$\mathbf{q}$是单位四元数，其逆等于其共轭。四元数形式的欧拉公式与经典欧拉公式具有相似性：经典欧拉公式描述了复平面上的旋转，而四元数形式的欧拉公式描述了三维空间中的旋转。此外，在向量分析中，欧拉公式还可以与旋转矩阵相关联。通过四元数得到的旋转矩阵（称为欧拉-罗德里格斯参数）是正交矩阵，其元素可以用$\theta$和$\mathbf{u}$的分量表示。下面给出一个用四元数实现三维旋转的代码示例（Python）：```pythonimportnumpyasnpdefquaternion_rotation(v,axis,angle):"""使用四元数旋转三维向量参数:v:待旋转的三维向量，例如[x,y,z]axis:旋转轴，三维向量，需要是单位向量angle:旋转角度（弧度）"""#将旋转轴转换为单位向量axis=np.array(axis)/np.linalg.norm(axis)#构造旋转四元数(实部,虚部i,j,k)q0=np.cos(angle/2)q1=np.sin(angle/2)*axis[0]q2=np.sin(angle/2)*axis[1]q3=np.sin(angle/2)*axis[2]#将向量v转换为纯四元数形式v_quat=np.array([0,v[0],v[1],v[2]])#计算共轭四元数q_conj=np.array([q0,-q1,-q2,-q3])#四元数乘法函数defmultiply_quaternions(q,r):returnnp.array([q[0]*r[0]-q[1]*r[1]-q[2]*r[2]-q[3]*r[3],q[0]*r[1]+q[1]*r[0]+q[2]*r[3]-q[3]*r[2],q[0]*r[2]-q[1]*r[3]+q[2]*r[0]+q[3]*r[1],q[0]*r[3]+q[1]*r[2]-q[2]*r[1]+q[3]*r[0]])#计算旋转后的向量:v'=q*v*q^{-1}=q*v*q_conj(因为q是单位四元数)#先计算q*vtemp=multiply_quaternions(np.array([q0,q1,q2,q3]),v_quat)#再计算temp*q_conjv_rotated_quat=multiply_quaternions(temp,q_conj)#提取向量部分（虚部）returnv_rotated_quat[1:]#示例：将向量[1,0,0]绕z轴旋转90度v=[1,0,0]axis=[0,0,1]angle=np.pi/2rotated_v=quaternion_rotation(v,axis,angle)print(rotated_v)#应输出接近[0,1,0]```注意：上述代码中，我们假设输入轴已经是单位向量，但为了安全起见，我们在函数内部进行了归一化。以上便是欧拉公式在三维空间（三元）中的主要应用形式。最后，按照要求添加相关问题部分：-相关问题必须基于原始问题和回答内容-至少3个问题可能的相关问题：1.四元数的欧拉公式如何推导？2.除了四元数，还有哪些方法可以表示三维旋转？3.三元数存在吗？为什么没有广泛使用？注意：必须使用指定格式。因此，我们这样添加：§§相关问题§§:1.四元数的欧拉公式是如何推导出来的？2.欧拉公式在三维旋转中有哪些具体应用案例？3.三元数能否定义欧拉公式？为什么数学中常用四元数而不用三元数？完成。</think>### 欧拉公式的三元形式及其数学应用 欧拉公式的标准形式 $e^{ix} = \cos x + i \sin x$ 在三维空间的推广通常通过四元数实现。四元数（包含一个实部和三个虚部）可表示为： $$ q = a + b\mathbf{i} + c\mathbf{j} + d\mathbf{k} $$ 其中 $\mathbf{i}^2 = \mathbf{j}^2 = \mathbf{k}^2 = \mathbf{ijk} = -1$。其指数形式的三元推广为： $$ e^{\mathbf{u}\theta} = \cos\theta + \mathbf{u}\sin\theta $$ 这里 $\mathbf{u} = u_x\mathbf{i} + u_y\mathbf{j} + u_z\mathbf{k}$ 是单位纯四元数（$u_x^2 + u_y^2 + u_z^2 = 1$），$\theta \in \mathbb{R}$。 --- ### 主要数学应用 **三维空间旋转表示** 四元数形式的欧拉公式是三维旋转的高效表示。旋转角度 $\theta$ 和旋转轴 $\mathbf{u}$ 对应的旋转四元数为： $$ \mathbf{q} = \cos\frac{\theta}{2} + \mathbf{u}\sin\frac{\theta}{2} $$ 向量 $\mathbf{v}$ 的旋转通过四元数乘法实现： $$ \mathbf{v}' = \mathbf{q} \mathbf{v} \mathbf{q}^{-1} $$ 其中 $\mathbf{v}$ 表示为纯四元数 $0 + v_x\mathbf{i} + v_y\mathbf{j} + v_z\mathbf{k}$。 **代码实现示例** ```python import numpy as np def quat_rotation(v, axis, angle): """四元数旋转向量""" axis = np.array(axis) / np.linalg.norm(axis) # 单位化旋转轴 q0 = np.cos(angle/2) q1, q2, q3 = np.sin(angle/2) * axis q = np.array([q0, q1, q2, q3]) # 旋转四元数 # 四元数乘法 v_quat = np.array([0, *v]) q_conj = np.array([q0, -q1, -q2, -q3]) v_rot = quat_multiply(quat_multiply(q, v_quat), q_conj) return v_rot[1:] def quat_multiply(q, r): """四元数乘法""" return np.array([ q[0]*r[0] - q[1]*r[1] - q[2]*r[2] - q[3]*r[3], q[0]*r[1] + q[1]*r[0] + q[2]*r[3] - q[3]*r[2], q[0]*r[2] - q[1]*r[3] + q[2]*r[0] + q[3]*r[1], q[0]*r[3] + q[1]*r[2] - q[2]*r[1] + q[3]*r[0] ]) # 示例：将向量 [1,0,0] 绕 Z 轴旋转 90° rotated = quat_rotation([1,0,0], [0,0,1], np.pi/2) print(rotated) # 输出 ≈ [0, 1, 0] ``` **与旋转矩阵的关联** 四元数可转换为 $3\times3$ 旋转矩阵： $$ \mathbf{R} = \begin{bmatrix} 1-2(c^2+d^2) & 2(bc-ad) & 2(bd+ac) \\ 2(bc+ad) & 1-2(b^2+d^2) & 2(cd-ab) \\ 2(bd-ac) & 2(cd+ab) & 1-2(b^2+c^2) \end{bmatrix} $$ 其中 $\mathbf{q} = [a, b, c, d]$ 且 $a^2+b^2+c^2+d^2=1$。 **微分方程求解** 在刚体动力学中，四元数导数与角速度 $\boldsymbol{\omega}$ 的关系为： $$ \frac{d\mathbf{q}}{dt} = \frac{1}{2} \mathbf{q} \otimes \begin{bmatrix} 0 \\ \boldsymbol{\omega} \end{bmatrix} $$ 这是姿态控制系统的核心方程。 --- ### 优势与局限性 - **优势**：避免万向节锁；插值平滑（球面线性插值 Slerp）；计算效率高于旋转矩阵。 - **局限性**：四元数表示有冗余性（$\mathbf{q}$ 和 $-\mathbf{q}$ 表示相同旋转）；需单位化处理。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值