【数据结构】平衡树 _平衡树技巧-优快云博客

当我们存储和检索数据时，数据就像一个个物品，需要被合理地安排在树形结构中。普通的二叉搜索树在数据插入时，如果顺序不当，可能会退化成一条长长的链，就像把所有物品都堆在一条狭窄的通道上，检索起来效率极低。而平衡树则不同，它能巧妙地调整自身结构，让数据均匀分布，始终保持树的平衡状态，如同精心整理书架，将书籍分类摆放整齐，这样在查找特定书籍时就能快速定位。正是凭借这种维持平衡的能力，平衡树在数据存储和检索时极大地提高了效率，吸引了无数开发者和算法研究者的目光，接下来就让我们深入探索它的奇妙世界。

二、从二叉搜索树到平衡树

2.1 二叉搜索树的困境

在深入了解平衡树之前，我们先来认识一下它的 “前辈”—— 二叉搜索树（Binary Search Tree，BST）。二叉搜索树是一种特殊的二叉树，它的每个节点都含有一个键值，并且具有这样的性质：左子树中所有节点的键值都小于根节点的键值，右子树中所有节点的键值都大于根节点的键值，而左右子树又各自是一棵二叉搜索树。这就好比一个有序的家族族谱，长辈的辈分总是高于晚辈，左支的晚辈都比中间的长辈 “辈分低”，右支的晚辈则都比中间的长辈 “辈分高”。

二叉搜索树的插入操作就像是在族谱中添加新成员。新成员会从根节点开始比较键值，如果小于当前节点的键值，就往左子树走；如果大于，就往右子树走，直到找到一个合适的空位插入。查找操作类似，也是从根节点出发，通过不断比较键值，向左或向右子树深入，直到找到目标节点或者确定目标节点不存在。删除操作相对复杂一些，需要考虑被删除节点的子节点情况，确保删除后树的结构仍然符合二叉搜索树的性质。

在理想情况下，也就是二叉搜索树保持平衡时，它的高度大约为 logn（n 为节点数），插入、查找和删除操作的时间复杂度都能维持在 O (log n) ，效率相当高。然而，二叉搜索树有一个致命的弱点。当遇到一些极端情况，比如插入的数据是有序的，它就会退化成一个链表结构。原本层次分明的族谱变得像一条长长的单线传承，所有节点都在一条直线上，高度变为 n ，此时这些操作的时间复杂度也会退化为 O (n) ，效率大打折扣。比如我们依次插入 1、2、3、4、5，二叉搜索树就会变成一棵只有右子树的 “偏树”，查找 5 的时候，就需要从根节点 1 开始，逐个比较，经过 4 次比较才能找到，而不是平衡状态下的 log5 次。

2.2 平衡树的诞生

为了解决二叉搜索树在极端情况下性能急剧下降的问题，平衡树应运而生。平衡树可以看作是二叉搜索树的升级版，它在继承了二叉搜索树性质的基础上，增加了自平衡的能力。平衡树通过一系列复杂而巧妙的算法，在每次插入和删除节点后，自动调整树的结构，确保树的高度始终保持在对数级别，也就是 O (log n) 。这样一来，无论面对怎样的数据插入顺序，平衡树都能稳定地保持高效的操作性能，插入、查找和删除的时间复杂度始终被控制在 O (log n) ，就像一位训练有素的舞者，无论面对怎样复杂的舞步变化，都能保持优雅的姿态，不被绊倒。常见的平衡树有 AVL 树、红黑树等，它们各自有着独特的平衡策略和实现方式，接下来就让我们走进这些平衡树的奇妙世界，一探究竟。

三、常见平衡树类型剖析

3.1 AVL 树：严格平衡的代表

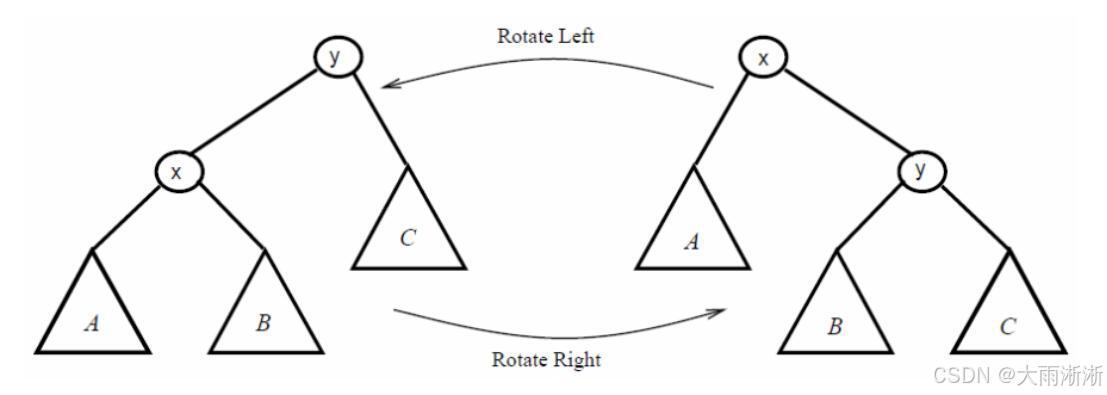
AVL 树是最早被发明的平衡二叉搜索树，它的名字来源于其发明者 G.M. Adelson-Velsky 和 E.M. Landis。AVL 树的平衡策略非常严格，它要求每个节点的左右子树高度差（也称为平衡因子）的绝对值不超过 1 。也就是说，对于 AVL 树中的任意一个节点，其左子树的高度减去右子树的高度，结果只能是 1、0 或者 -1。例如，在一棵 AVL 树中，某个节点的左子树高度为 3，那么它的右子树高度只能是 2、3，这样才能保证树的平衡。

当对 AVL 树进行插入或删除操作时，可能会破坏这种平衡。为了恢复平衡，AVL 树引入了旋转操作，主要有左旋、右旋、先左旋后右旋、先右旋后左旋这四种情况。以左旋为例，假设我们有一个节点 A，它的右子节点 B 的右子树高度较高，导致节点 A 的平衡因子变为 -2，此时就需要进行左旋操作。具体过程是将节点 B 提升为新的根节点，节点 A 变为 B 的左子节点，而 B 原来的左子节点则变为 A 的右子节点。这个过程就像是将一个倾斜的书架进行调整，把较高一侧的书移到另一侧，使书