八皇后的12组等效解

请使用回溯法编程，输出8皇后的所有解，并统计其中等效解的个数（所谓等效解是指，如果将解A 上下翻转，左右翻转，90度旋转等任意组合，如果能得到B，则称A和B为等效解）
要求：
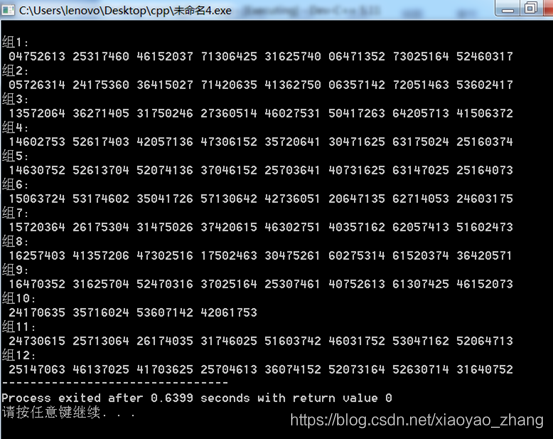
1.输出形式：如果有n个等价类
组1:共10个
(1,2,...,..x8)
......
组2：共...个

组n:共...个
.....

其中(x1,x2,..x8)的含义是在棋盘第1...8行中皇后的位置依次是x1...x8
2.实现建议：生成解后将解保存为无向图，求该图的连通分量

 

#include<iostream>
using namespace std;
#include<cstring>
#include<cmath>
#define N 8
int s=1; 
int sum=0,count=0,m=1,row=0;
int a[N][N],b[2*N][N],c[100][N],x[100];
//数组b[][]的第一个下标为不等效解得数目，第二个下标为8皇后所在列数 
void left90(int x[])
{
	for(int i=0;i<N;i++)
	a[row][N-1-x[i]]=i;
	row++;
}
void left180(int x[])
{
	for(int i=0;i<N;i++)
	a[row][N-1-i]=N-1-x[i];
	row++;
}
void left270(int x[])
{
	for(int i=0;i<N;i++)
	a[row][x[i]]=N-1-i;
	row++;
}
void store(int x[],int count)
{
	for(int i=0;i<N;i++)
	b[count][i]=x[i];
}
int test(int x[])
{
	int i,j;
	for(i=1;i<=m;i++)
	{
		for(j=0;j<N;j++)
		if(c[i][j]!=x[j]) break;
		if(j>=N) break;
	}
	if(i>m)return 1;
	else return 0;
}
int dx(int x[])
{
	int i,j,flag=0;
	for(int i=0;i<N;i++)
	a[row][i]=x[i];
	row++;
	for(int i=0;i<N/2;i++)
	if(x[i]+x[N-1-i]!=N-1)
	{flag=1;break;}
	
	if(N>4&&flag==0) left90(x);
	else if(flag)
	{left90(x); left180(x);left270(x);}
	for(int i=0;i<row;i++)
		for(j=0;j<N;j++)
			a[row+i][N-1-j]=a[i][j];
			cout<<endl;
	cout<<"组"<<s++<<":"<<endl; 
	for(int i=0;i<row*2;i++)
	{
		cout<<" ";
		for(j=0;j<N;j++)
		printf("%d",c[m][j]=a[i][j]);
		m++;
	}
}
int place(int k)
{
	for(int i=0;i<k;i++)
	if(x[i]==x[k]||abs(x[i]-x[k])==abs(i-k))
	return 0;
	return 1;
}
int backtrack(int t)
{
	int i,xx;
	if(t>N-1)
	{
		sum=sum+1;if(sum==1||test(x))
		{
			count++;
			store(x,count);
			row=0;
			dx(x);
		}
	}
	else for(i=0;i<N;i++)
	{
		x[t]=i;
		if(t==0&&x[t]>=N/2) break;
		if(place(t)==1)
		backtrack(t+1);
	}
}
int main()
{
	memset(x,0,sizeof(x));
	backtrack(0);
}