写在最前面:
本文只是对“Level Set Method and Dynamic implict Surfaces”这个文章的翻译,和添加自己的一点点的理解
正文开始:
1.4 Calculus Toolbox(积分工具箱)
characteristic function &Heaviside function
内部区域![]() 内的特征函数
内的特征函数![]() 有如下的定义方式:
有如下的定义方式: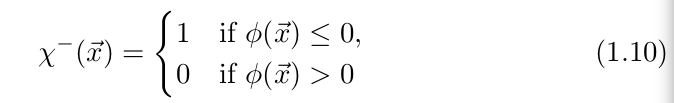
(我们把边界的情况包含到了公式1.10里面)
外部区域![]() 内的特征函数
内的特征函数![]() 有如下的定义方式:
有如下的定义方式:
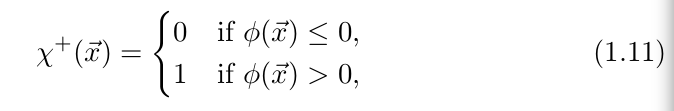
ps:个人觉得两个公式中的0那种情况,很鸡肋。既然已经在内部(或者外部)区域,度量符号的正负不是已经确定了吗?
当![]() 的维度变高,我们引入了Heaviside 函数:
的维度变高,我们引入了Heaviside 函数: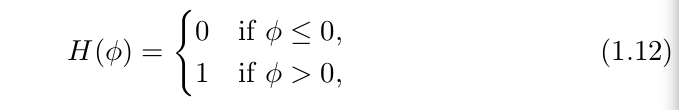
其中,度量函数![]() 的正负仍然是有
的正负仍然是有![]() 决定的。Heaviside函数同样也适用于地位的
决定的。Heaviside函数同样也适用于地位的![]() 因此Heaviside函数和特征函数的之间的转换关系如下:
因此Heaviside函数和特征函数的之间的转换关系如下:
![]()
volume integral function
1. 内部区域![]() 特征函数的积分:
特征函数的积分:
2.内部区域![]() Heaviside函数的积分:
Heaviside函数的积分: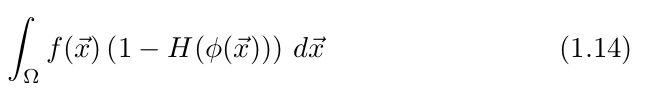
3. 外部区![]() 域Heaviside函数的积分:
域Heaviside函数的积分: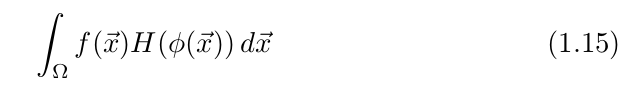
Dirac delta function
Heaviside函数在法向量![]() 方向上的方向导数的公式如下:
方向上的方向导数的公式如下:
1)![]() 为多维
为多维
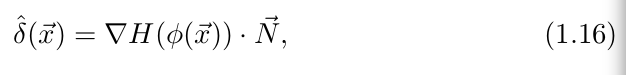
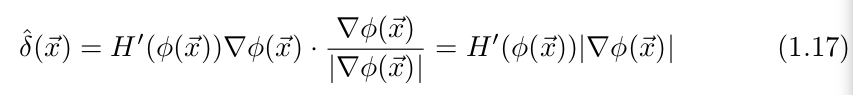
2)![]() 为一维
为一维

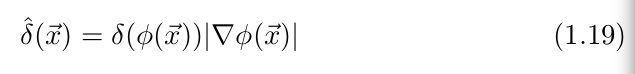
surface integral function
整个边界上的函数:
多维:
一维:
笛卡尔的网格需要对以上的公式进行重新定义:
smeared-out Heaviside function
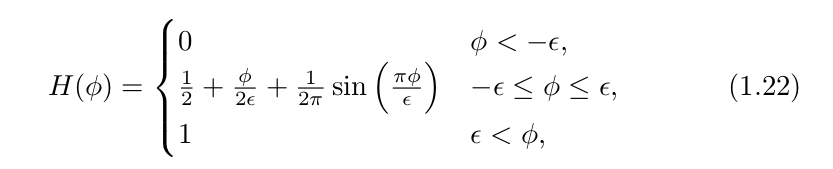
其中![]() 是一个可调参数,用于确定数值模糊网格带宽的大小。
是一个可调参数,用于确定数值模糊网格带宽的大小。
the derivative of the Heaviside function
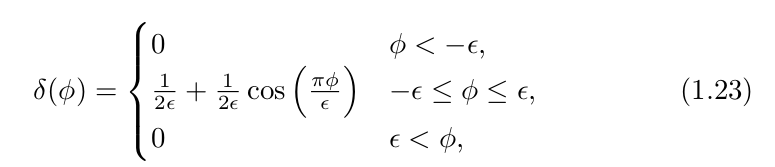




 本文深入探讨了Level Set方法与动态隐式表面的理论基础,详细解析了特征函数、Heaviside函数、体积积分函数、Dirac delta函数及表面积分函数等关键数学工具,并介绍了它们在高维空间中的应用。
本文深入探讨了Level Set方法与动态隐式表面的理论基础,详细解析了特征函数、Heaviside函数、体积积分函数、Dirac delta函数及表面积分函数等关键数学工具,并介绍了它们在高维空间中的应用。

















 1898
1898

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








