写在最前面:
本文只是对“Level Set Method and Dynamic implict Surfaces”这个文章的翻译,和添加自己的一点点的理解
正文开始:
1.4 Geometry Toolbox(几何工具箱)
已知一个确定边界,要判断某个点的位置,可通过以下的方法:
1)从该点处,投射到已知位于边界之外的某个遥远的位置。如果此时 这两点所连成的线,在边界上的焦点为偶数个,则为外部点在边界上的焦点为奇数个,则为内部点。
2) ![]() 这条等高线来作为边界,通过判断局部描述符
这条等高线来作为边界,通过判断局部描述符![]() 的正负来判断内外部。为正表示外部,为负表示内部。
的正负来判断内外部。为正表示外部,为负表示内部。
3) 当给出了一个点集的区间之后,再可以利用插值来判断一些正负。(但是数值型插值( numeriacal interpolation)有可能存在误差)
4)利用网格点集进行评估。其中要求我们的模糊函数足够的平滑,并且能通过网格来得到很好的解决
5) 用signed distance function 来表示表面
Boolean Operations

Gradient of the implicit function:
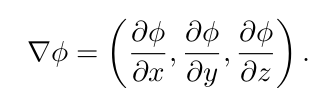
在某个零维边界点处的梯度评估是一个向量,这个向量与边界上的局部单位法向量方向相同。
单位法向量的表达式: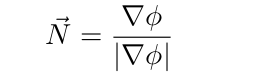
边界的模糊表示,在高维中同样适用。举例:
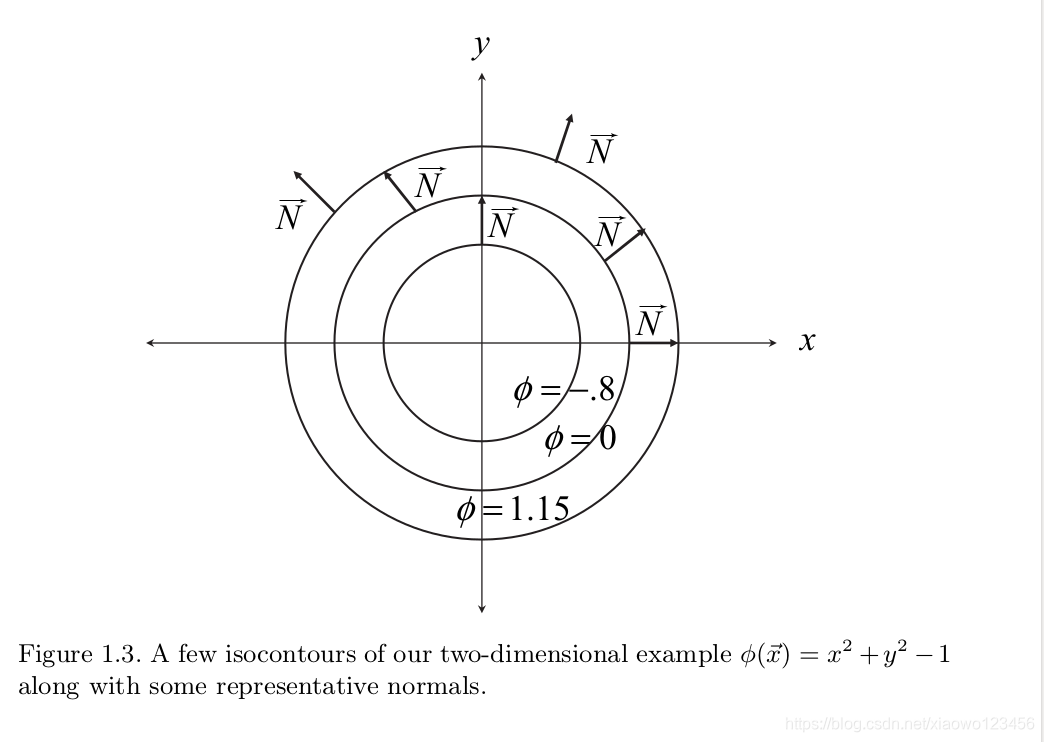
在x=0处,法向量时没有定义的,因此人为的将其定义为![]()
在我们的笛卡尔网格中,对于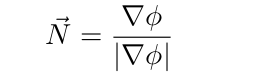 的导数,需要近似,我们采用一下的方法:
的导数,需要近似,我们采用一下的方法:
1) 一阶准确的前向差异 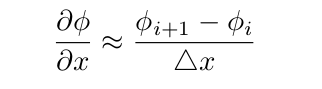
外部点的一阶准确的前向差异: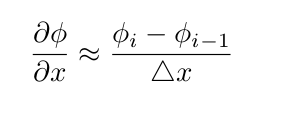
内部点的二阶准确的前向差异: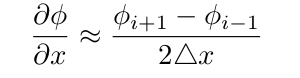
当所有数值计算的有限差异相同为零时,等式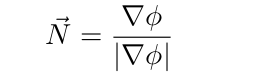 的分母消失。此时可以随机的选择法向量
的分母消失。此时可以随机的选择法向量
如果![]() 是平滑的良好函数,那么可以从在笛卡尔网格的节点处计算的N的值获得边界处法线的近似值。由此看到,
是平滑的良好函数,那么可以从在笛卡尔网格的节点处计算的N的值获得边界处法线的近似值。由此看到,![]() 这个度量函数的选择是十分紧要的。
这个度量函数的选择是十分紧要的。![]() 度量函数的选择问题,就是向量特征函数了。
度量函数的选择问题,就是向量特征函数了。
边界的平均曲率
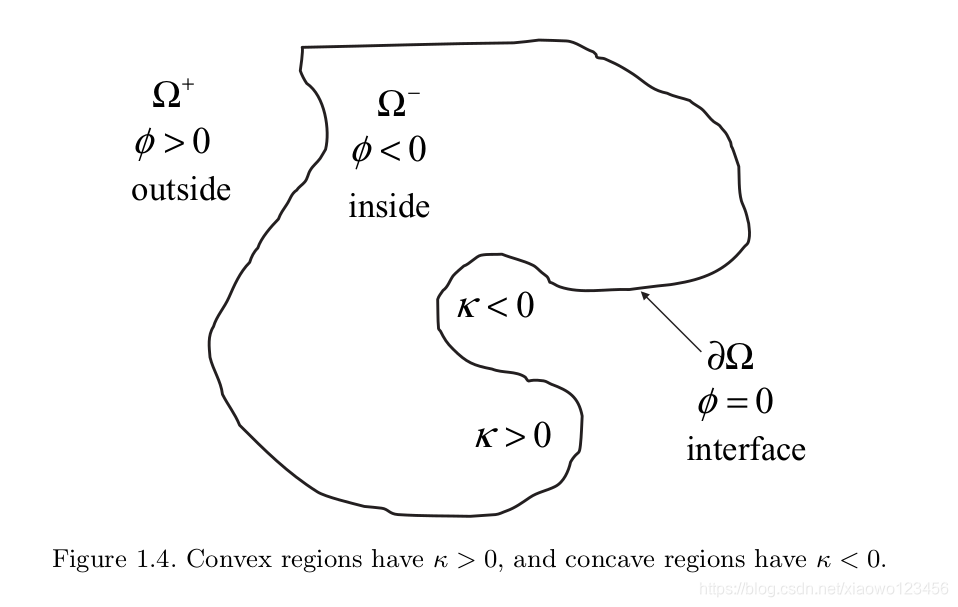
已知法向量为:![]()
曲率的计算公式为: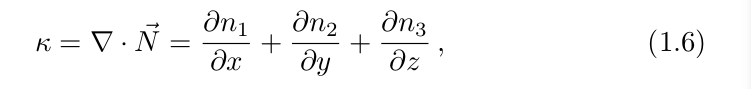
如上图可知, 当k>0时为凸,k<0时,为凹。 k=0时为平面。
用 来替代等式1.6,可以得到如下的曲率计算公式:
来替代等式1.6,可以得到如下的曲率计算公式: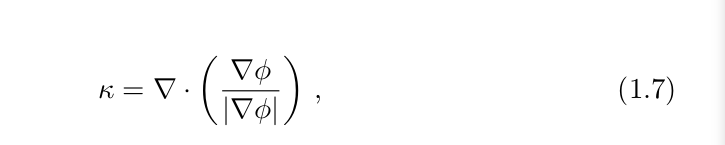 对这公司做一些带入,可以得到:
对这公司做一些带入,可以得到: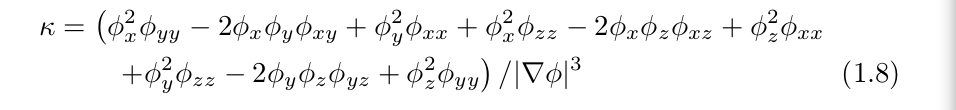
上面的公式,就看成二阶导数,和高阶混合偏导。
在笛卡尔网格的计算过程中,最小的测量单元就是:![]() ,并且我们把曲率限制在一个范围内:
,并且我们把曲率限制在一个范围内:![]() ,一旦有超出这个曲率范围的值,我们就用
,一旦有超出这个曲率范围的值,我们就用![]() 来替代。
来替代。




 本文介绍了 Level Set 方法及其在动态隐式表面的应用,包括几何工具箱的使用,如何判断点相对于边界的内外位置,以及边界表示、模糊函数的选择、曲率计算等关键概念。
本文介绍了 Level Set 方法及其在动态隐式表面的应用,包括几何工具箱的使用,如何判断点相对于边界的内外位置,以及边界表示、模糊函数的选择、曲率计算等关键概念。
















 1872
1872

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








