信息熵，联合熵，交叉熵，相对熵的概念与区别

各种熵之间的关系

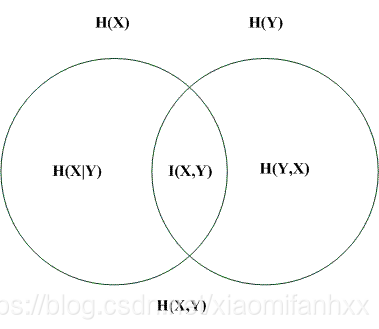
• H(X, Y) =  H(x) U H(Y);  —— 联合熵的定义：两个随机变量X,Y的联合分布，可以形成联合熵,是并集
• H(X|Y) = H(X, Y) - H(Y); H(Y|X) = H(X, Y) - H(X) —— 条件熵的定义
• H(X|Y) = H(X) - I(X, Y); H(Y|X) = H(Y) - I(X, Y)
• I(X, Y) = H(X) - H(X|Y) = H(X) + H(Y) - H(X, Y) —— 也可以作为互信息的定义
• 熵：H(X)=−∑xp(x)lnp(x)
  • 衡量不确定性的度量
• 联合熵: H(X,Y)=−∑x,yp(x,y)lnp(x,y)
  • （X,Y）在一起时的不确定性度量
• 条件熵: H(X,Y)−H(X)=−∑x,yp(x,y)lnp(y|x)
  • X确定时，Y的不确定性度量
  • 在X发生是前提下，Y发生新带来的熵。
• 交叉熵:H(p,q)=−∑xp(x)lnq(x)
  • 衡量p与q的相似性
• 相对熵: KL(p||q)=−∑xp(x)lnq(x)p(x)
  • p与q不相似的度量
  • KL(p||q)=−∑xp(x)lnq(x)p(x)
• H(X|Y) <= H(X)：
  • H(X)表示X的不确定度；H(X|Y)表示给定Y的情况下，X的不确定度。
  • 如果X与Y完全独立，则二者相等（给不给Y对X能给出多少信息无关）；
  • 而如果X与Y不是独立的，则给定Y之后会降低X的熵，即X的不确定性会降低

参考博客：

               联合熵：https://max.book118.com/html/2016/1202/67619413.shtm

               信息熵，条件熵，相对熵：https://www.cnblogs.com/kyrieng/p/8694705.html#name2

                互信息：https://blog.youkuaiyun.com/lk7688535/article/details/52529610