Zero-shot Learning 综述2

最新推荐文章于 2025-04-18 10:50:32 发布

小灰狼@花花

最新推荐文章于 2025-04-18 10:50:32 发布

阅读量736

点赞数

分类专栏： Zero-shot Learning 文章标签：计算机视觉机器学习人工智能深度学习

本文链接：https://blog.youkuaiyun.com/xiaohuilang6/article/details/116148747

版权

Zero-shot Learning 专栏收录该内容

6 篇文章

订阅专栏

3. 非线性映射

典型文章：Latent Embeddings for Zero-Shot Classification (LatEm)-2016 CVPR

通过一个隐变量，将SJE模型扩展为非线性

学习线性兼容函数并不特别适合于具有挑战性的细粒度分类问题。对于细粒度分类，需要一个能够自动将具有相似属性的对象分组在一起的模型，然后为每个组学习一个单独的兼容性模型。例如，可以分别学习两种不同的线性函数来区分棕色翅膀的蓝鸟和其他蓝色翅膀的蓝鸟。

主要贡献：

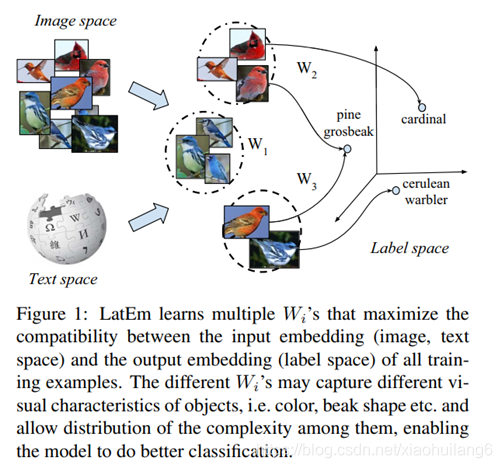
提出学习线性模型的集合，同时允许每个图像类别对从中进行选择。有效地模型非线性，因为在空间的不同局部区域，决策边界是线性的，是不同的；
提出通过模型裁剪的方式进行快速、有效的模型选择方法；
在三个具有挑战性的数据集上进行分段线性模型评估。

Latent Embedding Model

训练集：

x为图像嵌入后的特征向量（CNN或其他特征提取）

y为类别空间的嵌入（属性）

问题求解：

主要思想：合并潜在变量，决策函数分段线性化，达到非线性目的。

非线性兼容函数如下（与Latent SVM类似）：

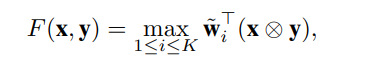
模型中单个线性模型的参数。

K≥2，隐变量选择的indices，i表示第i个线性模型

我们的主要目标是学习一组兼容空间使以下经验风险最小化：

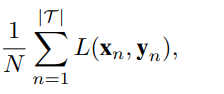
为对于给定输入（xn,yn）的损失函数。

Optimization

F是凸函数，这种分段模型不是连续凸函数，因此，此前线性模型中的优化方法在这里并不适用。为了解决这个问题，我们提出了一个简单的基于SGD的方法，其工作方式与凸函数的求解相同。

这样的模型的好处除了上面说的有更强的表达能力之外，LatEm由于拥有多个W，可以自适应地适应不同类型的样本，并且每个W 会有不同的关注点。

算法如下：

    def update_W(self, W, idx, train_classes):
        # train_classes: 训练集的类别id，共27个
        for j in idx:
            X_n = self.X_train[:, j]
            y_n = self.labels_train[j]
            y_ = train_classes[train_classes != y_n]
            picked_y = random.choice(y_)

            max_score, best_j = self.argmax_over_matrices(X_n, self.train_sig[:, picked_y], W)
            best_score_yi, best_j_yi = self.argmax_over_matrices(X_n, self.train_sig[:, y_n], W)

            if max_score + 1 > best_score_yi:
                if best_j == best_j_yi:
                    Y = np.expand_dims(self.train_sig[:, picked_y] - self.train_sig[:, y_n], axis=0)
                    W[best_j] = W[best_j] - self.args.lr*np.dot(np.expand_dims(X_n, axis=1), Y)
                else:
                    Y0 = np.expand_dims(self.train_sig[:, y_n], axis=0)
                    Y_pick = np.expand_dims(self.train_sig[:, picked_y], axis=0)
                    W[best_j] = W[best_j] - self.args.lr*np.dot(np.expand_dims(X_n, axis=1), Y_pick)
                    W[best_j_yi] = W[best_j_yi] + self.args.lr*np.dot(np.expand_dims(X_n, axis=1), Y0)
        return W

    def fit(self):

        print('Training...\n')

        best_val_acc = 0.0
        best_tr_acc = 0.0
        best_val_ep = -1
        best_tr_ep = -1

        rand_idx = np.arange(self.X_train.shape[1])  # 样本id的随机

        W = []
        for i in range(self.K):
            w = np.random.rand(self.X_train.shape[0], self.train_sig.shape[0]) *1.0 / np.sqrt(self.X_train.shape[0]) # W权重，[2048,85]
            # w = self.normalizeFeature(w.T).T
            W.append(w)
        W = np.array(W)

        train_classes = np.unique(self.labels_train)  # 共27个类别

        for ep in range(self.args.epochs):

            start = time.time()

            shuffle(rand_idx)

            W = self.update_W(W, rand_idx, train_classes)

            tr_acc = self.zsl_acc(self.X_train, W, self.labels_train, self.train_sig)
            val_acc = self.zsl_acc(self.X_val, W, self.labels_val, self.val_sig)

            end = time.time()

            elapsed = end - start

            print('Epoch:{}; Train Acc:{}; Val Acc:{}; Time taken:{:.0f}m {:.0f}s\n'.format(ep + 1, tr_acc, val_acc,
                                                                                            elapsed // 60,
                                                                                            elapsed % 60))

            if val_acc > best_val_acc:
                best_val_acc = val_acc
                best_val_ep = ep + 1
                best_W = np.copy(W)

            if tr_acc > best_tr_acc:
                best_tr_ep = ep + 1
                best_tr_acc = tr_acc

            if ep + 1 - best_val_ep > self.args.early_stop:
                print('Early Stopping by {} epochs. Exiting...'.format(self.args.epochs - (ep + 1)))
                break

        print('\nBest Val Acc:{} @ Epoch {}. Best Train Acc:{} @ Epoch {}\n'.format(best_val_acc, best_val_ep,
                                                                                    best_tr_acc, best_tr_ep))

        return best_W

Model selection

对于K的选取，有两种方法：

1.交叉验证；

2.基于剪枝的策略，该策略既具有竞争优势，又具有更快的训练速度。首先K取大值，并采用以下步骤修剪：

首先，对于每个样本，都选取一个线性模型进行评分，我们跟踪这些信息，并根据线性模型的数量建立一个直方图，计算每个线性模型被选择的次数。根据这个信息，在经过五次训练数据后，删除了选取次数不到选取5%的模型。

Decision

LatEm and SJE的不同：

1.LatEm为分段线性兼容函数，而SJE是线性的。不同的W针对不同的属性。

2.LatEm使用基于排序的损失，而SJE使用多类别损失。

4. 第三空间

典型文章：Zero-shot learning via semantic similarity embedding （SSE）-2015 ICCV

实现了保持语义一致性，还在保持语义一致性的同时，保持分类准确性。

上述介绍的方法，都是直接将视觉特征空间映射到语义空间来实现的，但是两个不同域的空间的语义差距较大，直接嵌入的效果仍不够理想，甚至会出现偏移。出于对齐两者空间、保持语义一致性的考虑，就有人提出了增加一个中间的共享空间（第三方空间），将两个空间都嵌入该空间里，并且同时进行优化以保持语义一致性。

源域（source domain）：每个类的语义描述

目标域（target domain）：视觉图像特征 (xn,yn)

本文算法依赖于以下假设：若目标域的混合比例和源域的混合比例相似，则他们来源于一个类别。

算法的目标是构建一个函数，对于一个任意的源域向量c和目标向量x（输入），将其嵌入到Δ|S| (直方图).

可见类y∈S，源域ψ(c)和目标域 π(x)特征嵌入（第三空间），表示类y在实例x,c上的比例

测试时，不可见类的源域向量

通过最大化直方图之间的语义相似度来预测x的不可见标签

其中< ·, ·>为内积

1.源域嵌入函数（ψ）：嵌入函数是通过一个与稀疏编码相关的参数优化问题来实现；

受稀疏编码的启发，源域的嵌入如下：

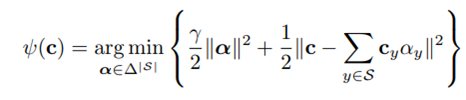
γ ≥ 0 预定义的正则化参数，||…||为l2范数。α = (αy)y∈S为不同可见类的贡献。c为源域向量。 Ψ是非线性的，由于单纯形约束，α向量中的小值被归零。交叉验证中，γ=10最好。

预测时，根据不可见类的属性向量cu，计算可以得到zu。

2.目标域嵌入函数（ π ）： πy(x)=< w, φy(x)>，φy(x)：类别相关的特征变换，W为权重。提出了一个基于边界的优化问题来联合学习权值向量和特征变换。请注意，参数化过程可能产生负值，并且可能不被规范化，这可以作为附加约束合并，但我们在优化目标中忽略了这个问题。

intersection函数捕获x低于每个阈值vy的数据，而ReLU捕获阈值以上的数据模式。从这个意义上说，这两个功能所产生的特性是互补的。这就是我们选择这两个函数来证明我们方法的鲁棒性的原因。

3.交叉验证：嵌入函数是参数独立的，我们通过使用交叉验证技术来选择这些参数。首先，在可见类上分别学习嵌入函数（剩余可见数据），然后联合优化源/目标嵌入函数的参数，以最大限度地减小已知类的预测误差，最后，在整个可见类数据集上重新训练参数。

Salient Aspects of Proposed Method:

1. 分解: 我们的方法试图将源和目标域实例分解为可见类的混合比例(直方图)。相比之下，现有的许多工作可以解释为学习源域属性和目标特征成分之间的跨域相似性。

2.类独立的特征变换πy(x)：分解的观点需要从根本上设计新的选择方法。例如πy(x) ，类y对应的组件需依赖于y，说明需要选择一个类独立的特征变换φy(x) ，因为W是常向量，与类别y无关（ πy(x)=< w, φy(x)> ）。

3.联合优化和不可见类的一般化：所提方法联合优化嵌入函数，以最好的对齐源域和目标域的直方图。即使对于固定参数，由于我们所学习的得分函数f(x,y)以一种复杂的方式连接源域和目标域，因此，嵌入函数π和ψ是非线性的映射。

Intuitive Justification of Proposed Method

我们的方法是基于将不可见的源实例和目标实例视为所见类比例的直方图。目标实例可以看作是由可见类（具有混合组件，取决于实例的位置）的混合而产生的。即假设 P和 Py分别是unseen和seen类的条件目标特征分布，那么：

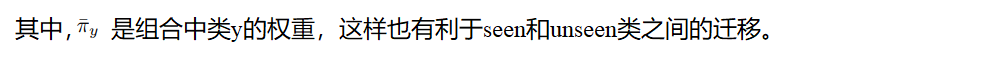
源域数据也可分解为源域可见类的混合（直方图）：

关键假设：如果目标域与源域都对应于相同的看不见的标签，目标域实例x必须具有与源域模式相似的平均混合模式。即π(x)的平均等于zu。注意，由于每个类只有单一源域向量，自然约束要求目标域中每个类对应的每个示例的混合的经验平均值与源域混合很好地匹配。

这里设target的类y的组合均值（average mixture,即中间空间）为πy，source对于类y 的中间空间表示为 zy，要求对于其他类别y’，即 y≠y’ 时，有

表示同一个类的两个domain的直方图尽可能对齐，同一个类的必须大于或等于其他类别的。

结构化得分函数为：

f是非凸的。

Max-Margin Formulation

目标函数：

这是一个二次规划问题，其中Eq.7 中w是target domain的映射权重矩阵，而 v 是source domain的，这两项起到正则的作用。

Eq. 8 就是用来衡量alignment loss的（即语义一致性的对齐），而Eq. 9 是衡量classification loss的（即分类）。

如果只考虑两个domain对齐，则有可能会造成误分类的情况，即图(a)；而如果只考虑分类的话，则可能没有完全对齐分布，即图(b)；所以本文的方法同时考虑了两者，既对齐分布又考虑分类，图(c)。

Alternating Optimization Scheme

1. 固定V学习w：根据Eq8和Eq9，求解Linear-SVM，学习w, ε, ξ

2. 固定w学习V：Concave-Convex procedure (CCCP)方法

Results：

未完，待续。。

参考文献：

[1] Xian Y, Akata Z, Sharma G, et al. Latent embeddings for zero-shot classification[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2016: 69-77.

[2] Zhang Z, Saligrama V. Zero-shot learning via semantic similarity embedding[C]//Proceedings of the IEEE international conference on computer vision. 2015: 4166-4174.