Deep Learning 4 -正则化

Deep Learning 4 -正则化（防止过拟合）

参考自：http://openclassroom.stanford.edu/MainFolder/DocumentPage.php?course=DeepLearning&doc=exercises/ex5/ex5.html

数据

数据地址：ex5Data.zip

数据包含两个数据集，一个用作线性回归，一个用作逻辑回归。同时也包含了一个函数map_feature.m，该函数用在逻辑回归中。

数据绘制

加载ex5Linx.dat和ex5Liny.dat。对应于x和y变量。

注意，输入x为单特征，因而可以作出x的二维图。

 

由上图可以看出，如果用一条直线拟合可能过于简单，因此，我们用一高阶的多项式以拟合更多的数据。如下：

 

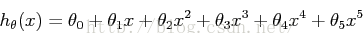
这意味着我们假设有六个特征，因为x0,x1,…x5是我们回归所用的特征。注意到即使使用了多项式进行拟合，这仍然是一线性回归问题，因为每个特征都假设是线性的。正则问题中，最小化损失函数为：

 

正则化参数λ是控制拟合程度的参数。由于适应性参数的增加，会对损失函数有一增加量。这个增加量与λ 和参数的平方有关。因此，λ项中不包含θ0。

一般方程

用一般方程可得到最佳参数，表达式如下：

 

λ项后的矩阵是(n+1)*(n+1)维，如上，（n是特征维度，不含截距项），y和矩阵x有相同的非正则回归的定义：

使用上述方程，利用下述不同的λ值求θ值：

1.      λ为0；

2.      λ为1；

3.      λ为10；

求解时，X是m*n+1为矩阵，因为有m组训练数据和n个特征，加上一截距项x0=1。第一列为1，其他列为相应的几次方，matlab中，

x = [ones(m, 1), x, x.^2, x.^3, x.^4, x.^5];

当求得θ值，除了列出θ向量中的元素θj外，也列出了θ的L2范数来确保求解的正确。Matlab中，可用norm(x)求范数。作图如下：

 

逻辑回归模型的正则化

第二部分的联系是用牛顿法求解正则化逻辑回归模型。首先，加载ex5Logx.dat和ex5logy.dat。这个数据集代表了逻辑回归问题的两个特征。为了和前面的进行区别，两个特征定义为u，v，因此在数据ex5Logx.dat中，第一列为u，作图时可作为横轴，第二列为v，可作为纵轴。

Matlab如下：

x = load('ex5Logx.dat'); 

y = load('ex5Logy.dat');

figure

% Find the indices for the 2 classes

pos = find(y); neg = find(y == 0);

plot(x(pos, 1), x(pos, 2), '+')

hold on

plot(x(neg, 1), x(neg, 2), 'o')

效果如下：

 

逻辑回归中的函数为：

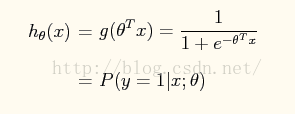
将参数θTx作为sigmod函数参数g(θTx)。

x为u、v由0-6次方组成：

 

因此，x有28个特征。

u是第一列，v是第二列。以后，x指的是x0，x1，而不是u，v。

为了节省x各项枚举的时间，Matlab中我们定义了函数'map_feature'，能够使原始的输入映射到特征向量。这个函数适用于单独的训练样本和整个训练集。调用时

x = map_feature(u, v)

正则化逻辑回归模型的损失函数为：

 

下面用牛顿法最小化函数。

牛顿法

更新规则为

 

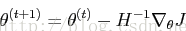
同非正则逻辑回归模型的牛顿法更新规则一直，但是现在要处理正则项，

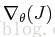和Hessian矩阵H如下：

 

如果λ为0，则同非正则的逻辑回归模型。

1.      xi为特征向量，28维；

2.      为28维向量；

3.      xi*(xi)T和H为28*28矩阵；

4.      yi和为标量；

5.      在非正则项中，后面的对角阵为28*28维；

下面运行牛顿法：

1.      λ为0；

2.      λ为1；

3.      λ为10；

为了确定时候收敛，每次迭代时记录J(θ)值。

收敛后，利用θ值求分类边缘。即：

 

Matlab中：

% Define the ranges of the grid

u = linspace(-1, 1.5, 200);

v = linspace(-1, 1.5, 200);

 

% Initialize space for the values to be plotted

z = zeros(length(u), length(v));

 

% Evaluate z = theta*x over the grid

for i = 1:length(u)

    for j =1:length(v)

        %Notice the order of j, i here!

       z(j,i) = map_feature(u(i), v(j))*theta;

    end

end

 

% Because of the way that contour plotting works

% in Matlab, we need to transpose z, or

% else the axis orientation will be flipped!

z = z'

% Plot z = 0 by specifying the range [0, 0]

contour(u,v,z, [0, 0], 'LineWidth', 2)

如下图：

 

由于有28个θ，将不显示结果的比对。但是可以用气2范数进行比对。

解决方案

线性回归代码在这里，逻辑回归代码在这里。

一般解：

 

随着λ增加，θ范数减小。这是由于λ越大，对较大的拟合参数惩罚大。

在第一幅途中，λ=0，意味着非正则线性回归。由于目标优化过程中仅最小化平方误差，这个曲线对于数据很合适，但并不能很好的反应一般趋势，是一种过拟合。

第二幅图显示过拟合减小在正则化参数增加到1后。由于过拟合的函数仍然是5阶多项式，因此曲线比第一幅图更简单。

第三幅图显示λ值过大。显示为少拟合，曲线并不遵从点的方向趋势。

牛顿法解：

下图是在牛顿法收敛后θ的范数。λ为0时经过15次迭代后收敛，在为1或10时经过5次迭代后收敛：

 

随着λ的增加，θ范数减小。在λ为0的途中，算法边缘拟合精度高，单仍然有1个点误判。这对于一般的分类来说精度过高。

λ为1时，图中显示了一个较小精度的边缘，该边缘仍然能够很好区分正负。

λ为10时，正则项过于高，导致边缘并不准确。