红黑树Red and Black binary tree--------BRtree

于 2022-03-17 19:59:45 发布
阅读量721 收藏 1
点赞数 3
文章标签： b树 数据结构 c++
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/xiaobai_hellow/article/details/123553221
版权
本文详细介绍了红黑树的概念，包括其定义、五大性质，以及在节点插入和删除过程中的调整策略。通过模拟实现展示了关键操作，如旋转和颜色调整，以保持红黑树的正确性。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

红黑树

红黑树的概念以及性质

1.红黑树的概念：
红黑树也是一种二叉搜索树，但是在每个节点上都增加了一个存储位存储节点的颜色，可以是red也可也是black，通过任何一条从根节点到子节点的路径中，根据红黑树着色方式的限制，没有任何一条路径是其他路径的两倍，因此，红黑树是接近平衡的。
2.红黑树具有五大性质：
①：每个节点不是红色就是黑色。
②：根节点是黑色的。
③：如果一个节点是红色的，那么它的两个子节点必然是黑色的。
④：对于每个节点，从该节点开始，到达其后代所有叶子节点的路径上黑节点数目是相同的。
⑤：每个叶子节点都是黑色的（此处的叶子节点指的是空节点）。
3.红黑树的优点：
由于在AVL树中，由于AVL树是绝对平衡的，所有在进行插入和删除的时候，为了维护其绝对的平衡性，有时候进行修改节点的操作，需要进行到根节点，旋转的次数比较多，所以出现了红黑树，当数据不是静态的数据而是动态的数据，进行插入和删除的时候就不用去维护绝对的平衡，也就减少了旋转的次数，照样可以提高效率，并且红黑树的平均查找效率还是log2（n）。

红黑树节点的插入和删除

1.节点的设置：
由于在红黑树中，我们需要让每个节点都赋予颜色，所以我们添加了枚举，而且与AVL树不同的是，我们将平衡因子去掉，增加了指向父节点的指针，
节点代码如下：

typedef enum{BLACK = 0,RED = 1}clour;
template<class Type>
class BRTreeNode
{
	friend class BRTree<Type>;
public:
	BRTreeNode(Type d = Type(),BRTreeNode<Type>* left = nullptr,
		BRTreeNode<Type>* right = nullptr,BRTreeNode<Type>* p = nullptr)
		:data(d), leftchild(left), rightchild(right), parent(p), _clour(RED)
	{}
	~BRTreeNode()
	{}
private:
	Type data;
	BRTreeNode<Type>* leftchild;
	BRTreeNode<Type>* rightchild;
	BRTreeNode<Type>* parent;
	clour _clour;
};

并且我们默认新加入的节点是红色的，这样有利于我们对节点进行修改。
2.插入操作
1.插入操作的步骤
①：找到要插入节点的位置，并进行插入。
②：对红黑树进行调整。
2.找到需要插入节点的位置与AVL树的相同，但是由于构造节点的时候，有指向其父节点的指针，所以我们就不需要使用栈结构进行操作。
3.对红黑树进行调整：
调整的时候，我们需要去寻找插入节点的叔伯节点（就是其父节点的兄弟节点），通过观察其叔伯节点的颜色，来判断要插入的节点应如何改变。
下面情况中，我们用x表示要插入的节点，p表示插入节点的父节点，时表示插入节点的叔伯节点，g表示插入节点的祖父节点，gg表示插入节点的曾祖父节点。
对红黑树进行调整，其中会遇到四个状况，分别如下：
1.s为黑色且x为外侧插入（就是和其父节点相相同，例如p为g的左子树，x围为p的左子树）。
遇到这个情况，我们只需先对p和g节点进行一次单旋转，然后更改p和g节点的颜色即可。如图：
在这里插入图片描述
此图为一个右单旋转的情况，如图，深色为黑节点，浅色为红节点，左单旋转也是如此，不过将图反转来就好了。
2.s为黑色且x为内侧插入（例如：p为g的左子树，x为p的右子树）。
遇到这个情况，我们首先要对x和p进行一次单旋转，并改变x和g的颜色，再对g做一次单旋转即可。
如图：
在这里插入图片描述
如图是一个先左转，再右转的一个例子，其中只改变了一次颜色，就是将x节点的颜色从红色变成了黑色。
3.s为红色且x为外侧插入。
此时对p和g做一次单旋转，并改变x的颜色，然后判断gg的颜色
①：如果gg颜色为黑色，那么一切搞定。
②：如果gg颜色为红色，那么就要看情况4
如图：
在这里插入图片描述
情况如图，如果此时gg节点为黑色节点，那么就完成了插入操作。
4.如果情况三过后，gg颜色为红色，那么我们就需要对在情况三的操作下，继续让节点向上回溯，并进行修改节点。
如图：
在这里插入图片描述
如果gg节点为红色，那么旋转完就会出现红红节点相连，不符合红黑树的性质，所以我们必须向上回溯，继续往上进行回溯调整。
重要的是：我们一般情况下不会对情况三和情况四进行上述操作，如果进行上述操作就有可能旋转到根节点，大大降低了效率，此时我们可以在遇到情况三的时候，不进行旋转，只进行改变颜色，将p和s都改为黑色，并将g改为红色，在让x指向g进行向上回溯，这样操作减少了循环，增加了效率。
3.删除操作
1.删除的步骤：
①：找到删除的节点，并进行删除。
②：删除后对红黑树进行调整。
2.找到节点进行删除的操作和AVL树是相同的，都是化二为一，被删除的节点最多只有一个子节点，所以我们就可以分为一下五种组合：
①：被删除的节点为红色节点，且没有左右子树。这个时候可以直接删除，因为删除这个节点完全不会影响红黑树的性质。
②：被删除的节点为黑色节点，且没有左右子树。这个时候问题会比较复杂，会涉及删除节点的兄弟节点颜色，来重新判断删除的方式。
③：被删除的节点为黑色节点，并且有一个子节点。可以判断出，有一个子节点根据红黑树的性质4，被删除的节点的子节点的颜色一定是红色的，所以我们只需要用被删除的节点的子节点与被删除节点进行替换，并将其替换的节点重新变为黑色即可。
④：被删除的节点右两个子节点，这个时候，我们需要化二为一，将其两个子节点变成一个子节点，和AVL树的删除操作相同，可以在被删节点的左子树找最大的节点与其替换，然后去其左子树删除该节点，也可以在被删节点的右子树去寻找最小的节点与其替换，然后在右子树去删除最小的节点即可。
3.此时我们看一下组合②的所有情况：
在组合二的情况中，我们需要对删除节点进行颜色调整，因为被删除的节点是黑色，如果删除之后，会导致该支路的路径少一个黑色节点，这样的情况会违背性质4，所以我们现在对删除的节点进行双色化，让其拥有两个黑色，这虽然违背了性质1，但是在最后的时候，将这一个黑色的情况删除即可。
在这里插入图片描述

组合二的情况可以分为以下四种情况:
①：被删节点的兄弟节点为黑色，并且带有一个同侧的红色子节点。
此时不管父的颜色，直接对父节点和兄弟节点进行一次单旋转，并且将父节点的颜色赋给兄弟节点，将被删节点的颜色赋给父节点即可。
如图：
在这里插入图片描述

②：被删节点的兄弟节点为黑色，并且带有一个不同侧的红色子节点。
此时先对兄弟节点的子节点和兄弟节点节点进行一次单旋转，并将其颜色进行修改，兄弟节点颜色变为红色，原来兄弟系欸但的子节点颜色变为黑色，然后再进行情况①即可。
如图：
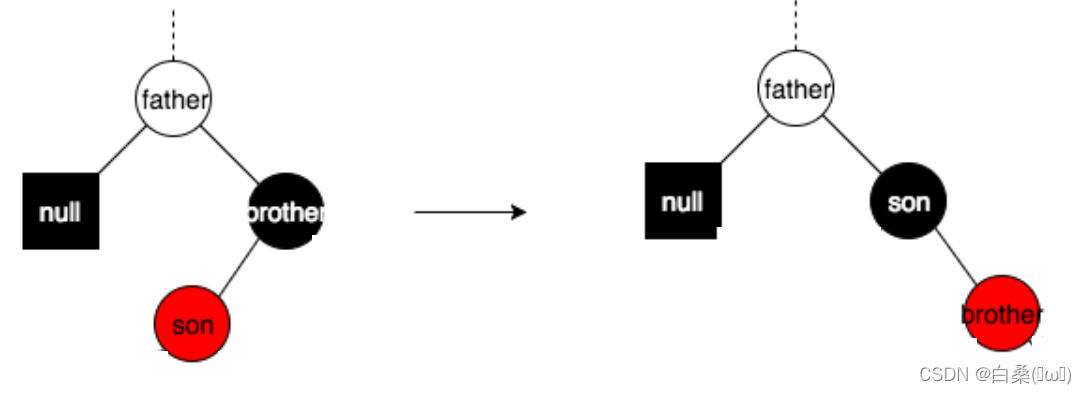
在这里插入图片描述

③：被删节点的兄弟节点为黑色，并且没有红色子节点。
此时又分为两种情况：
a.如果父节点的颜色为红色，那么直接将父节点的颜色变为黑色，将兄弟节点的颜色变为红色即可。
如图：
在这里插入图片描述

b.如果父节点的颜色为黑色，那么将被删节点的黑色附加给父节点上，不进行删除，并将原来的被删节点指向父节点，将父节点作为被删节点继续向上回溯，寻找错误。
如图：
在这里插入图片描述

④：被删节点的兄弟节点为红色，此时父节点一定为黑色。
此时将兄弟节点和父节点颜色进行互换，并对其进行一次单旋转，然后将兄弟节点重新指向被删节点的兄弟节点，此时就变成了情况1或者情况2的判断了。
如图：
在这里插入图片描述

红黑树的模拟实现

#include<iostream>
#include<vector>
using namespace std;
typedef enum{BLACK = 0,RED = 1}clour;
template<class Type>
class BRTree;
template<class Type>
class BRTreeNode
{
	friend class BRTree<Type>;
public:
	BRTreeNode(Type d = Type(),BRTreeNode<Type>* left = nullptr,
		BRTreeNode<Type>* right = nullptr,BRTreeNode<Type>* p = nullptr)
		:data(d), leftchild(left), rightchild(right), parent(p), _clour(RED)
	{}
	~BRTreeNode()
	{}
private:
	Type data;
	BRTreeNode<Type>* leftchild;
	BRTreeNode<Type>* rightchild;
	BRTreeNode<Type>* parent;
	clour _clour;
};
template<class Type>
class BRTree
{
public:
	BRTree() :Nil(_BuyNode()) ,root(Nil)
	{
		Nil->leftchild = Nil->rightchild = nullptr;
		Nil->_clour = BLACK;
	}
public:
	void Insert(const Type& v)
	{
		Insert(root, v);
	}
	void Remove(const Type& v)
	{
		Remove(root, v);
	}
protected:
	void I_AdjustBRtree(BRTreeNode<Type>* x,BRTreeNode<Type>*& t);
	void R_AdjustBRtree(BRTreeNode<Type>* x, BRTreeNode<Type>*& t);
	void Insert(BRTreeNode<Type>*& t, const Type& v);
	void Remove(BRTreeNode<Type>*& t, const Type& v);
	void RightRotate(BRTreeNode<Type>* pr,BRTreeNode<Type>*& t);
	void LeftRotate(BRTreeNode<Type>* pr,BRTreeNode<Type>*& t);
protected:
	BRTreeNode<Type>* _BuyNode(const Type& v = Type())
	{
		BRTreeNode<Type>* s = new BRTreeNode<Type>(v);
		s->leftchild = s->rightchild = Nil;
		return s;
	}
private:
	BRTreeNode<Type>* Nil;
	BRTreeNode<Type>* root;
};
template<class Type>
void BRTree<Type>::RightRotate(BRTreeNode<Type>* pr, BRTreeNode<Type>*& t)
{
	BRTreeNode<Type> *p = pr->leftchild;
	pr->leftchild = p->rightchild;
	if (p->rightchild != Nil)
		p->rightchild->parent = pr;
	p->parent = pr->parent;
	if (pr->parent == Nil)
		t = p;
	else if (pr->parent->leftchild == pr)
		pr->parent->leftchild = p;
	else
		pr->parent->rightchild = p;
	p->rightchild = pr;
	pr->parent = p;	
}
template<class Type>
void BRTree<Type>::LeftRotate(BRTreeNode<Type>* pr, BRTreeNode<Type>*& t)
{
	BRTreeNode<Type>* p = pr->rightchild;
	pr->rightchild = p->leftchild;
	if (p->leftchild != Nil)
		p->leftchild->parent = pr;
	p->leftchild = pr;
	if (pr->parent == Nil)
		t = p;
	else if (pr->parent->leftchild == pr)
		pr->parent->leftchild = p;
	else
		pr->parent->rightchild = p;
	p->parent = pr->parent;
	pr->parent = p;
}
template<class Type>
void BRTree<Type>::I_AdjustBRtree(BRTreeNode<Type>* x, BRTreeNode<Type>*& t)
{
	while (x->parent->_clour == RED)
	{
		BRTreeNode<Type>* s;
		if (x->parent == x->parent->parent->leftchild)
		{
			s = x->parent->parent->rightchild;
			if (s->_clour == BLACK)//状况1和状况2
			{
				if (x == x->parent->rightchild)//状况2的双旋转判断
				{
					x = x->parent;
					LeftRotate(x,t);
				}
				x->parent->_clour = BLACK;//先变色，再旋转
				x->parent->parent->_clour = RED;
				RightRotate(x->parent->parent,t);
				break;
			}
			else//状况3（简便算法），避免状况4的出现
			{
				x->parent->_clour = s->_clour = BLACK;
				x->parent->parent->_clour = RED;
				x = x->parent->parent;
			}
		}
		else
		{
			s = x->parent->parent->leftchild;
			if (s->_clour == BLACK)
			{
				if (x == x->parent->leftchild)
				{
					x = x->parent;
					RightRotate(x,t);
				}
				x->parent->_clour = BLACK;
				x->parent->parent->_clour = RED;
				LeftRotate(x->parent->parent,t);
				break;
			}
			else
			{
				x->parent->_clour = s->_clour = BLACK;
				x->parent->parent->_clour = RED;
				x = x->parent->parent;
			}
		}
	}
	t->_clour = BLACK;
}
template<class Type>
void BRTree<Type>::Insert(BRTreeNode<Type>*& t, const Type& v)
{
	//1.寻找插入的位置
	BRTreeNode<Type>* x = t,*p = Nil;
	while (x != Nil)
	{
		if (v == x->data)//插入元素不符合
			return;

		p = x;//找到要插入位置的父节点

		if (x->data > v)
			x = x->leftchild;
		else
			x = x->rightchild;
	}
	x = _BuyNode(v);
	if (p == Nil)//证明插入的是第一个节点
	{
		t = x;
		t->parent = Nil;
	}
	else if (p->data > x->data)//x在p的左子树插入
	{
		p->leftchild = x;
	}
	else
	{
		p->rightchild = x;//x在p的右子树插入
	}
	x->parent = p;//将x的父节点指针指向其父节点
	//2.修改树
	I_AdjustBRtree(x,t);
}
template<class Type>
void BRTree<Type>::R_AdjustBRtree(BRTreeNode<Type>* x, BRTreeNode<Type>*& t)
{
	while (x != t && x->_clour == BLACK)
	{
		BRTreeNode<Type>* s;
		if (x == x->parent->leftchild)//左子树的删除
		{
			s = x->parent->rightchild;
			if (s->_clour == RED)//情况四，父节点一定为黑色，此时将s和其父节点旋转，就变成情况1，2，3中的一种了
			{
				s->parent->_clour = RED;
				s->_clour = BLACK;
				LeftRotate(s->parent, t);
				s = x->parent->rightchild;
			}
			if (s->_clour == BLACK && s->leftchild->_clour != RED && s->rightchild->_clour != RED)
				//情况3，若被删节点兄弟节点为黑且没有红色子树
			{
				s->_clour = RED;
				if (x->parent->_clour == RED)//若父节点为红色，则直接将兄弟节点的颜色改成红色和父节点的颜色改为黑色
				{
					x->parent->_clour = BLACK;
					x = t;//中止循环
				}
				else      //若父节点为黑色，将兄弟节点颜色修改为红色，并向上回溯
				{
					x = x->parent;
				}
			}
			else
			{
				if (s->leftchild->_clour == RED)//情况2，被删除节点的兄弟节点内测有一个红色节点（双旋转）
				{
					s->leftchild->_clour = BLACK;
					s->_clour = RED;
					s = s->leftchild;
					RightRotate(s->parent, t);
				}

				//情况1，被删除节点的兄弟节点有一个同方向的红色子节点（单旋转）
				s->_clour = x->parent->_clour;
				x->parent->_clour = x->_clour;
				s->rightchild->_clour = BLACK;
				LeftRotate(x->parent, t);
				x = t;
			}
		}
		else//右子树的删除
		{
			s = x->parent->leftchild;
			//情况四，被删除节点的兄弟节点是红色的
			if (s->_clour == RED)
			{
				s->parent->_clour = RED;
				s->_clour = BLACK;
				RightRotate(s->parent, t);
				s = x->parent->leftchild;
			}
			//情况三，被删除的节点的兄弟节点没有红色子节点
			if (s->_clour == BLACK && s->leftchild->_clour != RED && s->rightchild->_clour != RED)
			{
				s->_clour = RED;
				if (s->parent->_clour == BLACK)
				{
					s->parent->_clour = BLACK;
					x = t;
				}
				else
				{
					x = x->parent;
				}
			}
			//情况2，被删节点的兄弟节点有一个与其反方向的红色节点
			else
			{
				if (s->rightchild->_clour == RED)
				{
					s->_clour = RED;
					s->rightchild->_clour = BLACK;
					s = s->rightchild;
					LeftRotate(s, t);
				}
				//情况1，被删节点的兄弟节点有一个与其同方向的红色节点
				s->_clour = x->parent->_clour;
				x->parent->_clour = x->_clour;
				s->leftchild->_clour = BLACK;
				RightRotate(x->parent, t);
				x = t;
			}
		}
	}
}
template<class Type>
void BRTree<Type>::Remove(BRTreeNode<Type>*& t, const Type& v)
{
	//1.找到需要删除的节点
	//if (t == Nil)//如果树为空
		//return;
	BRTreeNode<Type>* p = t,*q = Nil;
	while (p != Nil)
	{
		if (p->data == v)
			break;

		if (p->data < v)
			p = p->rightchild;
		else
			p = p->leftchild;
	}
	if (p == Nil)//证明没找到
	{
		return;
	}
	if (p->leftchild != Nil && p->rightchild != Nil)//化二为一
	{
		q = p->leftchild;
		while (q->rightchild != Nil)
			q = q->rightchild;
		p->data = q->data;
		p = q;
		/*if (p->leftchild != Nil)//其左子树一定为Nil
			q = p->leftchild;
		else*/
	}
	if (p->leftchild != Nil)
		q = p->leftchild;
	else
		q = p->rightchild;
	q->parent = p->parent;
	if (q->parent == Nil)
		t = q;              //情景1，要删除的是红节点，且没有左右子树，直接删除
	else if (p->parent->leftchild == p)
		p->parent->leftchild = q;
	else
		p->parent->rightchild = q;
	//2.进行修改
	if (p->_clour != RED)//证明删除的节点一定是黑的，那么这个节点就只有两种情况，要么p只有一个子节点，并且为红色
		//要么删除的节点没有子节点
	{
		if (q != Nil)//证明p有一个子节点，并且这个字节带你一定是红的，直接删除然后替换就可以了
			q->_clour = BLACK;
		else//证明删除的节点一定是黑的，且没有子节点
			R_AdjustBRtree(q, t);
	}
	delete p;
}
评论 1
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值