【算法刷题-第4题】付账问题-python

目录

题目描述

输入描述

输出描述

输入输出样例

题解

代码

---

题目描述

有n个人出去吃饭，他们总共消费了S元。其中第i个人带了ai元。

所有人带的钱的总数是足够付账的。现在问题来了：每个人分别要出多少钱呢？ 为了公平起见，我们希望在总付钱量恰好为S的前提下，最后每个人付的钱的标准差最小。 我们约定，每个人支付的钱数可以是任意非负实数，即可以不是1分钱的整数倍。

你需要输出最小的标准差是多少。

标准差：是多个数与它们平均数差值的平方平均数，一般用于刻画这些数之间的“偏差有多大”。设第i个人付的钱为bi元，那么标准差为：

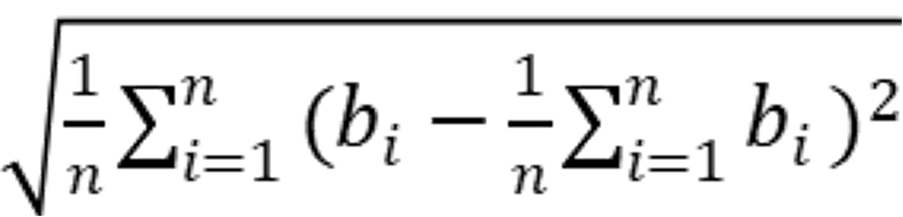
输入描述

从标准输入读入数据。

第一行包含两个整数 n、S；
第二行包含 n 个非负整数 a1, ..., an。

输出描述

输出最小的标准差，四舍五入保留 4 位小数。
保证正确答案在加上或减去 10^−9 后不会导致四舍五入的结果发生变化。

输入输出样例

输入

5 2333
666 666 666 666 666

 输出

0.0000

题解

1. 首先分析标准差，这个标准差的意思其实就是

（当前这个人付的钱 - 应该平均给的钱）²，然后每个人相加，最后 / 总人数

2. 也就是说，要想这个标准差最小，每个人给的钱都应该接近平均数才对

3. 但是有的人钱少，有的人钱多，这个时候该怎么办呢？？？

4. 于是我们想想，分了两种情况：

•         钱不够： 那肯定全部付完呗
•         钱多了： 付的也多，但是总和只有那么多，所以应该让后面钱多的人平摊剩下的钱，这样更接近我们的平均数

5. 然后最开始的时候，就应该排序，这样我们去遍历的时候，就可以很好的实现上面的两种方式，也就是先让钱不够的给付了来，然后再去付剩下的平均数

6. 于是代码如下：

代码

n,s = map(int,input().split())  
a = list(map(int,input().split()))
a.sort()  # 排序
avg = s/n  # 平均值
sum0 = 0
for i in range(len(a)):
  if a[i] * (n-i) < s:   # 当前这个人的钱不够
    sum0 += math.pow(a[i]-avg,2)
    s-= a[i]
  else:
    cur_avg = s/(n-i)    # 剩下所有人要付的钱的平均数
    sum0+= math.pow(cur_avg - avg,2) * (n-i)
    break
print("{:.4f}".format(math.sqrt(sum0/n)))

这里主要解释一下：

a[i] * (n-i) < s： 当前的人付的钱 * 剩下的所有人 = 此时所有人付的钱，也就是说，以这个人的钱当平均数的时候，钱是不够的，所以要全部付，也就是从局部接近平均数推向整体接近平均数。

如果这个地方判断 a[i] < avg，那么会出现一个问题，也就是当前这个数或许比总的平均数要大，但是在计算后面的总体平均数的时候，你当前这个数不一定比剩下钱的平均数要大，此时如果再付它所有钱，那么肯定是不正确的。

所以，这里主要就是，如果你：当前的钱*后面所有人 > 剩余的钱，那么此时，你可以让后面的所有数都取剩余钱的平均数，这样更加接近整体的平均数，也就是最后算出来的那个标准差更小