hdu1506 Largest Rectangle in a Histogram（思维）

最新推荐文章于 2024-06-30 10:57:50 发布

原创最新推荐文章于 2024-06-30 10:57:50 发布 · 218 阅读

0 ·

CC 4.0 BY-SA版权

思维专栏收录该内容

37 篇文章

订阅专栏

本文探讨了如何在直方图中寻找最大的矩形面积，通过优化算法提高效率。介绍了直方图问题背景，详细解释了算法思路，并对比了两种算法实现方式，展示了优化后的代码在处理大规模数据时的性能提升。

Largest Rectangle in a Histogram

Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 24040 Accepted Submission(s): 7527

Problem Description

A histogram is a polygon composed of a sequence of rectangles aligned at a common base line. The rectangles have equal widths but may have different heights. For example, the figure on the left shows the histogram that consists of rectangles with the heights 2, 1, 4, 5, 1, 3, 3, measured in units where 1 is the width of the rectangles: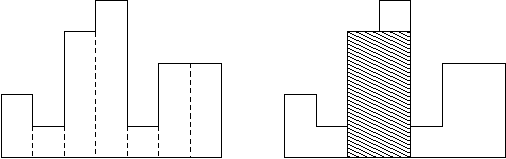

Usually, histograms are used to represent discrete distributions, e.g., the frequencies of characters in texts. Note that the order of the rectangles, i.e., their heights, is important. Calculate the area of the largest rectangle in a histogram that is aligned at the common base line, too. The figure on the right shows the largest aligned rectangle for the depicted histogram.

Input

The input contains several test cases. Each test case describes a histogram and starts with an integer n, denoting the number of rectangles it is composed of. You may assume that 1 <= n <= 100000. Then follow n integers h1, ..., hn, where 0 <= hi <= 1000000000. These numbers denote the heights of the rectangles of the histogram in left-to-right order. The width of each rectangle is 1. A zero follows the input for the last test case.

Output

For each test case output on a single line the area of the largest rectangle in the specified histogram. Remember that this rectangle must be aligned at the common base line.

Sample Input

7 2 1 4 5 1 3 3 4 1000 1000 1000 1000 0

Sample Output

8 4000

Source

University of Ulm Local Contest 2003

Recommend

LL | We have carefully selected several similar problems for you: 1505 1069 1087 1058 1176

这道题转化成：a[i]*(L[i]-R[i])。L【i】表示比她大的最左边的位置，R【i】是比她大的最右边的。

（思维）

然后记忆优化一下就行了。

代码：

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int INF=0x3f3f3f3f;
const int maxn=500000;

LL a[maxn],L[maxn],R[maxn];
int main()
{
    int n;
    while(scanf("%d",&n)){
        if(n==0)
            break;
        memset(L,0,sizeof(L));
        memset(R,0,sizeof(R));
        for(int i=1;i<=n;i++){
            scanf("%lld",&a[i]);
        }
        LL ans=-INF;
        LL qian,hou;
        L[1]=1;
        R[n]=n;
        LL lala;
        for(int i=2;i<=n;i++){
            qian=i;
            while(qian>1 && a[i]<=a[qian-1]){
                qian=L[qian-1];
            }
            L[i]=qian;
        }
        for(int i=n-1;i>=1;i--){
            hou=i;
            while(hou<n && a[i]<=a[hou+1])
                hou=R[hou+1];
            R[i]=hou;
         ///   cout<<L[i]<<"  && "<<R[i]<<endl;
        }
        for(int i=1;i<=n;i++){
             LL sum=(R[i]-L[i]+1)*a[i];
            ans=max(ans,sum);
        }
        printf("%lld\n",ans);

    }
    return 0;
}

上边循环里的优化很好。

下边是超时代码，更好体现：

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int INF=0x3f3f3f3f;
const int maxn=500000;

LL a[maxn],L[maxn],R[maxn];
int main()
{
    int n;
    while(scanf("%d",&n)){
        if(n==0)
            break;
        memset(L,0,sizeof(L));
        memset(R,0,sizeof(R));
        for(int i=1;i<=n;i++){
            scanf("%lld",&a[i]);
        }
        LL ans=-INF;
        LL qian,hou;
        for(int i=1;i<=n;i++){
            qian=i-1;
            while(qian>=1 && a[i]<=a[qian])
                qian--;
            L[i]=qian+1;
            hou=i+1;
            while(hou<=n && a[i]<=a[hou])
                hou++;
            R[i]=hou-1;
         ///   cout<<L[i]<<"  && "<<R[i]<<endl;
            LL sum=(R[i]-L[i]+1)*a[i];
            ans=max(ans,sum);
        }
        printf("%lld\n",ans);

    }
    return 0;
}