hiho：#1176 : 欧拉路·一

最新推荐文章于 2020-09-26 10:13:04 发布

原创最新推荐文章于 2020-09-26 10:13:04 发布 · 227 阅读

0 ·

CC 4.0 BY-SA版权

图论专栏收录该内容

40 篇文章

订阅专栏

本文介绍了一款解密游戏中如何利用欧拉路的概念来帮助角色收集所有道具的方法。通过判定回路及节点度数来确定是否存在一条路径能够遍历所有桥梁。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

#1176 : 欧拉路·一

时间限制: 10000ms

单点时限: 1000ms

内存限制: 256MB

描述

小Hi和小Ho最近在玩一个解密类的游戏，他们需要控制角色在一片原始丛林里面探险，收集道具，并找到最后的宝藏。现在他们控制的角色来到了一个很大的湖边。湖上有N个小岛(编号1..N)，以及连接小岛的M座木桥。每座木桥上各有一个宝箱，里面似乎装着什么道具。

湖边还有一个船夫，船夫告诉主角。他可以载着主角到任意一个岛上，并且可以从任意一个岛上再载着主角回到湖边，但是主角只有一次来回的机会。同时船夫告诉主角，连接岛屿之间的木桥很脆弱，走过一次之后就会断掉。

因为不知道宝箱内有什么道具，小Hi和小Ho觉得如果能把所有的道具收集齐肯定是最好的，那么对于当前岛屿和木桥的情况，能否将所有道具收集齐呢？

举个例子，比如一个由6个小岛和8座桥组成的地图：

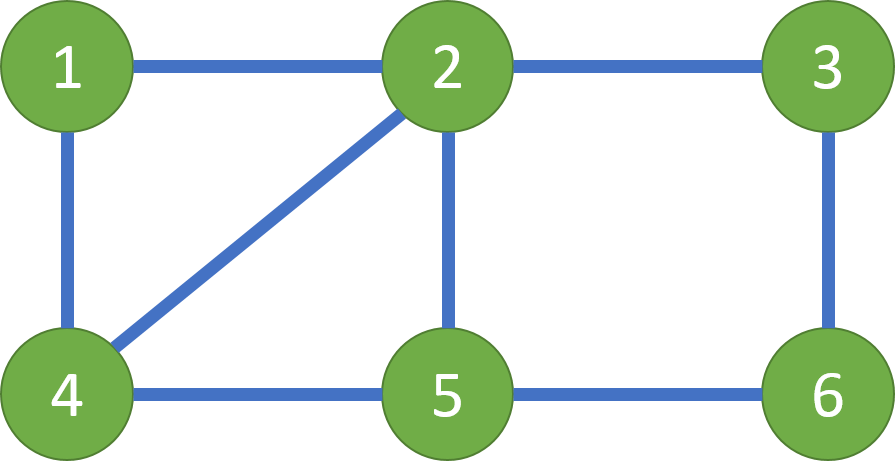
主角可以先到达4号小岛，然后按照4->1->2->4->5->6->3->2->5的顺序到达5号小岛，然后船夫到5号小岛将主角接回湖边。这样主角就将所有桥上的道具都收集齐了。

提示：欧拉路的判定

输入

第1行：2个正整数，N,M。分别表示岛屿数量和木桥数量。1≤N≤10,000，1≤M≤50,000

第2..M+1行：每行2个整数，u,v。表示有一座木桥连接着编号为u和编号为v的岛屿，两个岛之间可能有多座桥。1≤u,v≤N

输出

第1行：1个字符串，如果能收集齐所有的道具输出“Full”，否则输出”Part”。

样例输入

样例输出：Full思路：显然是欧拉通路（每个点都走，且每条边走一遍）。求欧拉通路的方法：1.判断是否是一个回路（即通过并查集findset（））2.判断每个点的度（degree）是否全为偶数。满足条件1，全为偶数的话就是。3.或者有两个点是奇数度。复习了一遍欧拉通路。代码：

#include<iostream>
#include<stdio.h>
#include<string.h>
using namespace std;
const int maxn=50000+100;
int n,m;
int degree[maxn];
int fa[maxn];
int findset(int i)
{
    if(fa[i]==-1)
        return i;
    return fa[i]=findset(fa[i]);
}
void init()
{
    memset(degree,0,sizeof(degree));
    memset(fa,-1,sizeof(fa));
}
int main()
{
    int u,v;
    while(~scanf("%d%d",&n,&m))
    {
        init();
        for(int i=1;i<=m;i++)
        {
            scanf("%d%d",&u,&v);
            degree[u]++;
            degree[v]++;
            u=findset(u);
            v=findset(v);
            if(u!=v)
                fa[u]=v;
        }
        int cnt=0;
        for(int i=1;i<=n;i++)
        {
            if(findset(i)==i)
                cnt++;
        }
        int cnt2=0;
        for(int i=1;i<=n;i++)
        {
            if(degree[i]%2==1)
                cnt2++;
        }
        if(cnt==1&&(cnt2==0||cnt2==2))
            printf("Full\n");
        else
            printf("Part\n");
    }
    return 0;
}