【MindSpore易点通】模型训练中的梯度下降

简介

在机器学习和深度学习中，需要对训练中的模型构建损失函数，这样才能在训练过程中找到最优的参数。梯度下降法是较常使用的优化算法，在求解过程中，需要求解损失函数的一阶导数。

通俗理解就是：

1. 从loss的某一点出发；
2. 找到当前最陡的坡（找梯度最大的方向）；
3. 朝最陡方向走一步（一次迭代后，一步的大小为步长）；
4. 循环执行2和3，走到最低点。

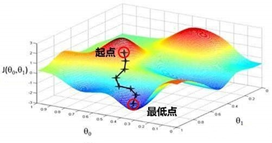
常见的梯度下降有三种不同的计算方法：批量梯度下降（Batch Gradient Descent）、随机梯度下降（Stochastic Gradient Descent）以及小批量梯度下降（Mini-Batch Gradient Descent）。接下来，我们将对这三种不同的梯度下降法进行探讨。

梯度下降的基本过程

以简单的线性回归模型为例：

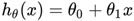
1、假设数据集中有m个样本，那么损失函数就是

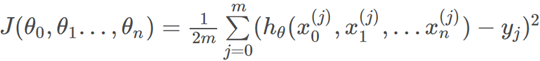
2、初始化θ0,θ1，...,θm, 算法终止距离ε，以及步长α。可以将所有的θ初始化为0， 将步长初始化为1。那么当前位置损失函数的梯度为：