lucene中的模糊检索包括:前缀查询、正则查询、通配符查询、字符类型范围查询,它们的实现原理类似,都是基于一个叫做“确定性有穷自动机(Deterministic Finite Automaton)”实现的,简称DFA。有穷自动机分为确定型有穷自动机(DFA)跟不确定型有穷自动机(NFA)。这两者一般作为正则表达式的引擎存在。正则表达式规则很好理解,但是正则表达式中的?,*,.等只是一种标识,并不能直接进行字符匹配,这种标识需要转化为计算机识别的模型,DAF和NFA一般用于构建这种模型,也称为正则表达式引擎。已有的正则表达式语言对应的引擎的类型有:

Lucene的模糊检索的实现是基于DFA,所以本篇文章将介绍DFA(确定型有穷自动机)原理及lucene的实现。
- DFA
DFA是一种非常有力的工具,可以看做是一个有向带权图,由节点、权重、边组成。其中图的节点集合称为自动机的状态集合,图的权值集合称为自动机的字符集合,图的边称为自动机的转换集合。此外,自动机还需指定初始状态和终止状态。下面是一个DFA的描述:
如果要判断一个字符串是不是仅仅由字符a和b组成,并且b是成对出现的。当然完成这样一个判断很简单,可以使用如下代码实现,不需要DFA也可以,但是如果我们考虑使用DFA来判断,看看实现的思路是怎么样的。

首先,该规则的正规表达式描述是:(a|bb)*。星号运算代表重复若干次,包括零次。
图一:

图一是DFA对上述规则的表示图,其中状态1为初始状态,在状态1上,还没有违反上述规则,因为只有a的字符串是满足规则的。因此,经过字母a以后还可以回到状态1。经过字母b到了状态2就不能回到状态1了,状态2表示“待定的”状态,在这个状态时不能肯定字符串是非法的,但也不是合法的,比如“ab”是不是合法的得取决于下面一个字符是a还是b。在状态2上,如果下一个字母是b,就回到了合法的状态也就是状态1。如果是字母a,到达状态3,那么就不能回到状态1了,则该字符串肯定是非法的。
从上图可知一个确定型有穷自动机包括:
- 一个有穷的状态集合,记作Q。
- 一个有穷的输入符号集合,记作Σ。
- 一个转移函数,以一个状态和一个输入字符作为变量,返回一个状态,记作δ。转移函数实在编程中比较重要的一环,给出当前状态和任一字符,输出为一个目标状态,接着便可以根据这个输出状态的类型,便可判断字符是否合法。
- 一个初始状态q,是Q状态之一。
- 一个终结状态或接受状态的集合F。集合F是Q的子集。
通常用缩写DFA来指示确定型有穷自动机。最紧凑的DFA表示是列出上面5个部分,DFA可以用西面的五元组表示:
A = (Q,Σ,δ,q,F)
其中A是DFA的名称,Q是状态集合,Σ是输入符号,δ是转移函数,q是初始状态,F是接受状态集合。
Lucene中使用DFA的地方有字符类型范围查询、前缀查询、正则查询、通配符查询,这几种查询的实现方式大致类似,下面分别介绍。
字符类型范围查询
Lucene中字符类型和数值类型的范围查询有不同的处理,数值类型有“大小”,不能和字符类型一同处理。
索引数据:

范围查询:
![]()
查询范围为(“bc”,”hcq”),对应的DFA转移图为:

上图是对查询范围为(“bc”,”hcq”)状态机的完整的描述,其中状态0是一个初始状态,状态1是一个可接受状态。
1.1转移函数
1)状态0发出三个方向,对应着三种转换,分别转换到状态1、状态2、状态3。

2)状态1是一个可接收状态,即到状态1意味着当前字符串是满足要求的。所以范围是0-255。

3)状态2是中间状态,只有到状态1一种转换。

4)状态3对应两种转换,固有两个转移函数。
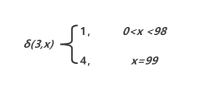
5)同上。

6)状态5是一个终结状态,故没有转移函数。
1.2判断过程
1)判断abc
“a”的ASCII码为97,无法通过转移函数完成转移,所以"a"不在查询范围内。
2)判断bed

b经过状态0判断转换到状态2,由于99<e<255,所以转换到状态1,状态1是可接受状态,无论be后面是什么都是合法字符。
3)判断cef

由于c在b h中间所以由状态0转换到状态1,进入可接受状态,之后的字符便进入状态1自旋状态,属于合法字符。
4)判断hcq

hcq显然沿着0->3->5到达中介状态满足要求是合法字符
5)判断hcqr
hcqr达到终结状态5之后还有一个字符r,由于是终结状态,没有对应转换,所以hcqr是不合法字符。
- 代码实现
2.1构建状态转移图
状态转移图的构建实在termRangQuery初始化时构建的

toAutomaton方法是入口

其中makebinaryInterval完成了状态转移图,该方法较长,分为几个部分来看,
第一部分:

首先创建一个自动机对象,状态信息和转移图时保存在自动机对象中的。

从Automaton可以看到,创建了两个数组和一个bitset(isAccept),用于标识每一个状态是不是可接受状态,states数组用于存储状态,transitions存储具体的状态转移图,接着创建一个初始状态0,创建一个状态的代码实现的很简单,递增新增一个state并在states数组中标记一下,便将state值返回。

然后创建可接受状态1,并将对应的状态为标记为1。因为范围查询最终肯定是有一个可接受状态的。因为达到可接受状态之后便认为当前匹配已经结束,之后再有更多的内容,都只是在状态1 上自旋。所以接下来建立一个1->1的转换,对应的label为0-255。
第二部分:
下面的两个for循环,循环处理范围查询中边界值中的每一个字符,建立对应的状态转移图。
循环处理lower:
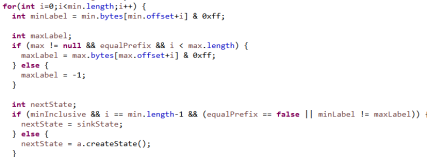
循环处理upper:
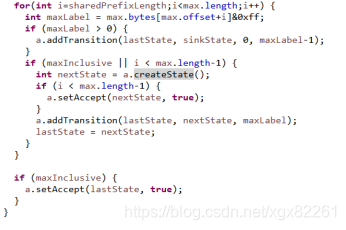
状态转移图的在内存中是存储在字节数组transitions中,添加一个transition代码如下:

需要存储transition的源state、目标state、最大值和最小值。对于查询条件 bc <= value <=hcq,生成的transitions数组为:
[1, 0, 255, 2, 98, 98, 1, 99, 103, 3, 104, 104, 1, 101, 255, 1, 0, 98, 4, 99, 99, 1, 0, 112, 5, 113, 113, 0, 0, 0],配合着states数组最终就生成了如下状态转移图。

转移图就构建完成了。
2.2 构建转移函数
TermRangeQuery父类AutomatonQuery中构建了状态转移函数。

最终是在实例化runAutomaton时创建了转移函数。转移函数的工作其实很简单,就是通过源state和任意字母找到目标state。

首先通过两层for循环找到转移图中的每个label和源state找到对应的目标state,然后放到一个int数组transitions中,关键代码是:
int dest = a.step(n, points[c]);
transitions[n * points.length + c] = dest;
这个时候可以通过transitions数组找到每个转移图的中每个label对应的目标state ,但是如何找到每个字母对应的目标state呢?lucene通过一个classmap数组给所有的字母进行编号。对于查询条件 be <= value <=hcq,生成的classmap为:
| b | c | d | e | f | g | h | i | j | k | l | m | n | o | p | q | r | s | t | u | ... |
| 1 | 2 | 3 | 4 | 4 | 4 | 5 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 7 | 8 | 8 | 8 | 8 | ... |
其中红色的字母是在转移图中出现的,黑色的字母是未出现的,遇到红色的编码+1,黑色的保持不变,这样保持不变的就可以拥有和前面字母一样的状态,那么在查询的时候就可以根据classmap 和 transitions来定位,查询的代码为:

Transitions:数组内容:
| 0 | -1 | 2 | 1 | 1 | 1 | 3 | -1 | -1 | -1 | -1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | -1 |
| 2 | -1 | -1 | -1 | -1 | 1 | 1 | 1 | 1 | 1 | -1 | 3 | 1 | 1 | 4 | -1 | -1 | -1 | -1 | -1 | -1 | -1 |
| 4 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 5 | -1 | -1 | 5 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 |
2.3转移函数查询流程
1)其实lucene对转移函数的实现就是结合上面classmap和Transitions两个数组进行的,可以通过两个数组确定每一个字符对应的目标状态。
2)目标状态为直到目标状态为可接受状态1和终结状态5,查询就结束了。
下面举几个查询的例子。
例子1:hcqr
根据上面的转移图可知,hcqr是不满足查询条件be <= value <=hcq。
查询的过程如下:
查询h:
Step(0,h) =>3
查询c:
Step(3,c) =>4
查询q:
Step(4,q) =>5
查询r:
Step(5,r) =>-1
其实从上面的数组中可以发现,状态5都是-1也就是说,状态5之后再有字符的话就是非法字符了。
例子二:hw
根据上面的转移图可知,hw是不满足查询条件be <= value <=hcq。
查询的过程如下:
查询h:
Step(0,h) =>3
查询w:
Step(3,w) =>-1
从上图可知,经过状态3之后还能是合法字符的字母只能是,b和c,也就是状态转移图中的状态3对应的两个transition:3->1、3->4
例子三:hcd
根据上面的转移图可知,hcd是满足查询条件be <= value <=hcq。
查询的过程如下:
查询h:
Step(0,h) =>3
查询w:
Step(3,c) =>4
查询d:
Step(4,d) =>1
最终是可以达到可接受状态1的,即hcd是合法字符串。
前缀查询/通配符查询
由于实现和字符范围查询类似,在此只给出例子的转移图。
前缀查询示例:
PrefixQuery quer = new PrefixQuery(new Term("city", "bc"))
状态转移图:

通配符查询示例:
WildcardQuery quer = new WildcardQuery(new Term("content", "*b*"))
状态转移图:

借鉴:https://www.amazingkoala.com.cn/Lucene/gongjulei/2019/0417/51.html

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








