Java实现队列以及队列的相关面试题

目录

• Java实现队列
• 队列的经典题目

---

 1.Java实现队列

1.1.概念

队列 ：只允许在一端进行插入数据操作，在另一端进行删除数据操作的特殊线性表，队列具有先进先出的特点 ：进行插入操作的一端称为 队尾( Rear) 出队列: 进行删除操作的一端称为 队头（Front）

因为Queue是一个接口，所以不能自己实例化，所以需要通过链表和数组两种方式来实现它，，，

链表实现（较简单）：

public class MyLinkedList {
    static class Node {
        public int val;
        public Node next;
        public Node(int val) {
            this.val = val;
        }
    }

    public Node head;
    public Node last;
    public int usedSize;
    /**
     * 入队
     */
    public void offer(int val) {
        Node node = new Node(val);
        if(this.head == null) {
            this.head = node;
            this.last = node;
        } else {
            this.last.next = node;
            this.last = node;
        }
        this.usedSize++;
    }

    /**
     * 出队
     */
    public int poll() {
        if(isEmpty()) {
            throw new MyLinkedListIsEmpty("队列为空！");
        }
        int val = this.head.val;
        this.head = this.head.next;
        //处理一个结点的情况
        if(this.head == null) {
            this.last = null;
        }
        this.usedSize--;
        return val;
    }

    /**
     * 出队，，但是不删除
     */
    public int peek() {
        if(isEmpty()) {
            throw new MyLinkedListIsEmpty("队列为空！");
        }
        return this.head.val;
    }
    public int size() {
        return this.usedSize;
    }
    public boolean isEmpty() {
        return usedSize == 0;
    }

}

数组实现（比上面那个难）：

public class MyCircularQueue {
    private int elem[];
    private int front;
    private int rear;
    public static final int DEFAULT_SIZE = 5;

    public MyCircularQueue() {
        this.elem = new int[DEFAULT_SIZE];
    }
    /**
     * 入队
     */
    public boolean enQueue(int value) {
        if(isFull()) {
            return false;
        }
        this.elem[this.rear] = value;
        this.rear = (this.rear + 1) % this.elem.length;
        return true;
    }

    /**
     * 出队
     */
    public int deQueue() {
        if(isEmpty()) {
            throw new MyCircularQueueIsEmpty("对列为空");
        }
        int val = this.elem[this.front];
        this.front = (this.front + 1) % this.elem.length;
        return val;
    }

    /**
     * 获取对头元素
     */
    public int Front() {
        if(isEmpty()) {
            return -1;
        }
        return this.elem[this.front];
    }

    /**
     * 得到队尾元素
     */
    public int Rear() {
        if(isEmpty()) {
            return -1;
        }
        return this.rear == 0 ? this.elem[this.elem.length - 1] : this.elem[rear - 1];
    }
    public Boolean isEmpty() {
        return this.rear == this.front;
    }
    public Boolean isFull() {
        return (this.rear+1)%this.elem.length == this.front;
    }
}

这里要注意两个点：

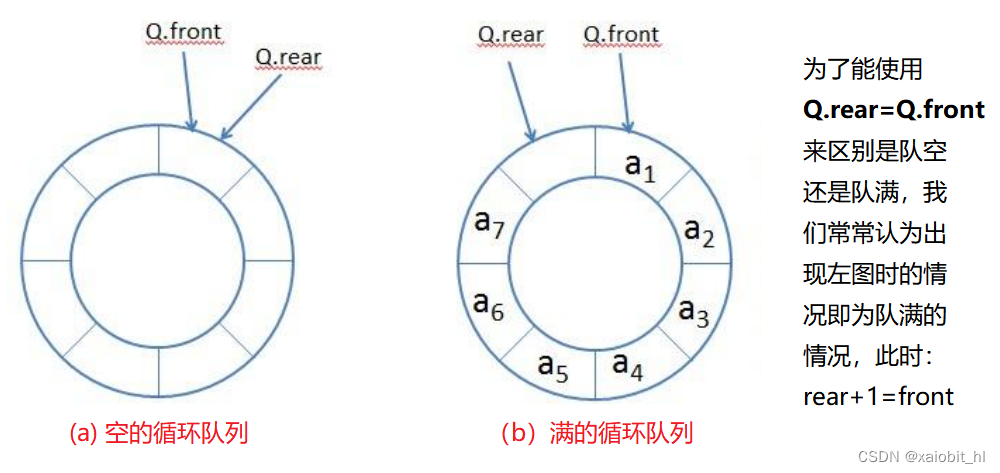
1.就是图中文字描述：我们为了让 rear == front 用来判断队空，所以我们在循环队列里空一个位置；当然不止有这一种方法可以区别，我们还可以用计数器来判断：rear == front时，count或usedSize不为0，则队列不为空；

2.我们这里要用到一个公式：下图中  a7 下标如何走到 a1 下标，也就是说正常情况我们的 a7 下标为 6 ，走到下一个元素一般是 ++ ，但是这里 a1 下标为 0，这样就做不到了，所以rear -> front 就有这样一个公式：(rear+1) % array.length ; 当然对头往后走一步，也需要这样处理才合理，，

 2.队列的经典题目

2.1.用队列实现栈

class MyStack {

    private Queue<Integer> queue1;
    private Queue<Integer> queue2;

    public MyStack() {
        queue1 = new LinkedList<>();
        queue2 = new LinkedList<>();
    }
    
    public void push(int x) {
        if(!queue1.isEmpty()) {
            queue1.offer(x);
        } else if(!queue2.isEmpty()){
            queue2.offer(x);
        } else {
            queue1.offer(x);
        }
    }
    
    public int pop() {
        if(queue1.isEmpty() && queue2.isEmpty()) return -1;
        if(!queue1.isEmpty()) {
            int size = queue1.size();
            for(int i = 0; i < size - 1; i++) {
                int tmp = queue1.poll();
                queue2.offer(tmp);
            }
            return queue1.poll();
        } else {
            int size = queue2.size();
            for(int i = 0; i < size - 1; i++) {
                int tmp = queue2.poll();
                queue1.offer(tmp);
            }
            return queue2.poll();
        }
    }
    
    public int peek() {
        if(empty()) return -1;
        if(!queue1.isEmpty()) {
            int size = queue1.size();
            int tmp = 0;
            for(int i = 0; i < size; i++) {
                tmp = queue1.poll();
                queue2.offer(tmp);
            }
            return tmp;
        } else {
            int size = queue2.size();
            int tmp = 0;
            for(int i = 0; i < size; i++) {
                tmp = queue2.poll();
                queue1.offer(tmp);
            }
            return tmp;
        }
    }
    
    public boolean empty() {
        return queue1.isEmpty() && queue2.isEmpty();
    }
}

用队列实现栈，我们是需要准备两个队列的，不然无法做到；

1.push函数:  我们把元素都放在一个队列里头，也就是谁不为空就放谁，这里规定一下都为空的时候放queue1，当然，你也可以放queu2；

2.pop函数：先把不为空的队列 queue1 倒出 size-1 个元素  到 queue2 中,然后弹出剩下的那个元素；

 3.peek函数：将不为空的队列 queue1 中的所有元素倒入 queue2 队列中，然后返回 queue.peek();当然，我这里是把每一个倒出来的元素都存在了一个 tmp 变量中，所以我只需要返回 tmp 变量；

 4.empty函数：两个队列都为空就返回true；

---

2.2.用栈实现队列

class MyQueue {

    private Stack<Integer> stack1;
    private Stack<Integer> stack2;
    public MyQueue() {
        stack1 = new Stack<>();
        stack2 = new Stack<>();
    }
    
    public void offer(int x) {
        stack1.push(x);
    }
    
    public int poll() {
        if(isEmpty()) {
            return -1;
        }

        if(!stack2.empty()) {
            return stack2.pop();
        } else {
            int size = stack1.size();
            for(int i = 0; i < size; i++) {
                int tmp = stack1.pop();
                stack2.push(tmp);
            }
            return stack2.pop();
        }
    }
    
    public int peek() {
        if(isEmpty()) {
            return -1;
        }
        if(!stack2.empty()) {
            return stack2.peek();
        } else {
            int size = stack1.size();
            for(int i = 0; i < size; i++) {
                int tmp = stack1.pop();
                stack2.push(tmp);
            }
            return stack2.peek();
        }
    }
    
    public boolean isEmpty() {
        if(stack1.empty() && stack2.empty()) {
            return true;
        }
        return false;
    }
}

同样的，用栈实现队列，我们也需要两个栈，实现起来也是很相似的；

1.offer函数：我们规定一下入队都入在在stack1中，出队都出stack2中的元素；

2.poll函数：我们有两种情况：如果stack2中无元素，则把stack1中的元素全部倒入stack2中；

如果stack2中有元素，则直接出stack2中的元素；

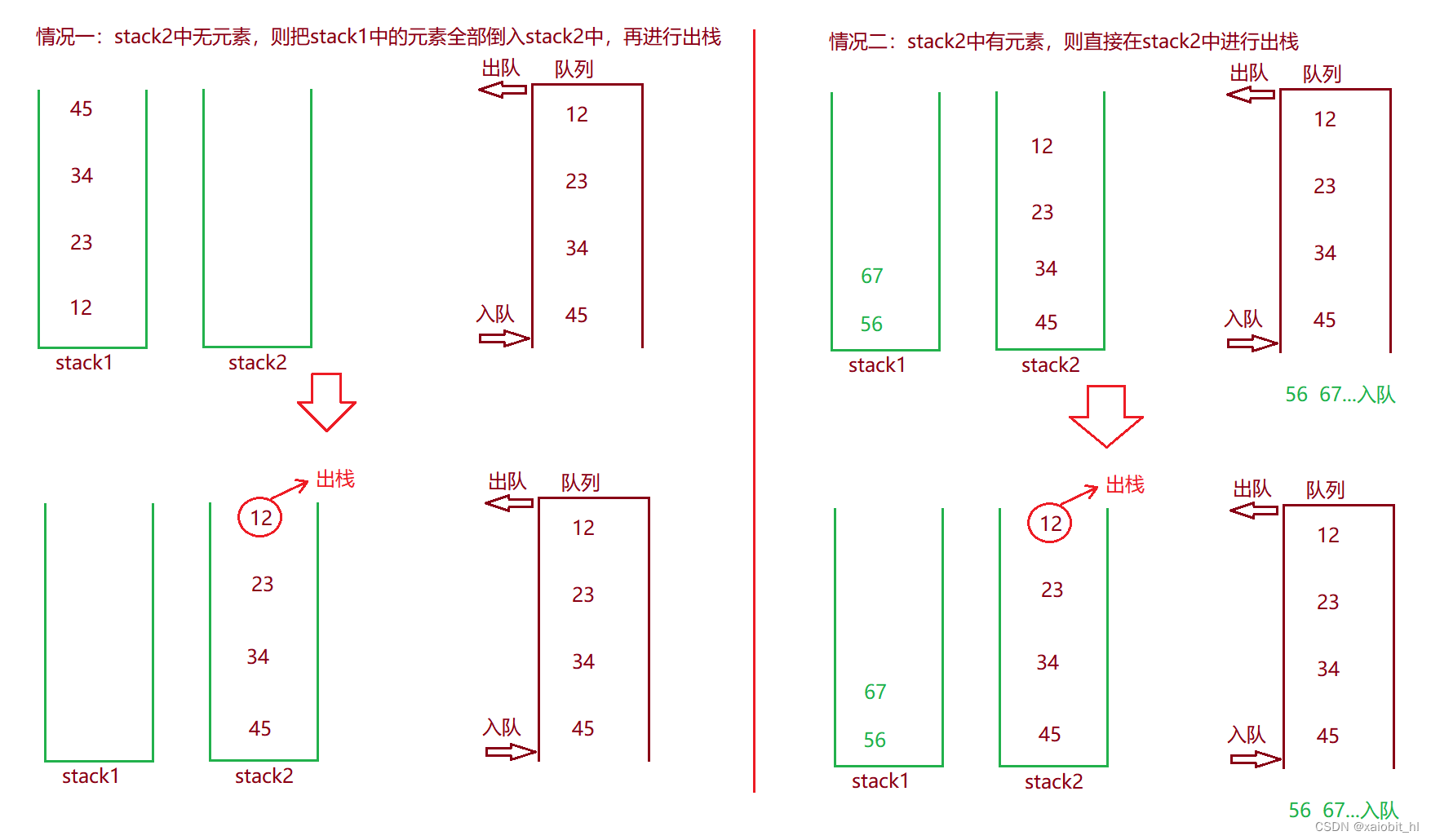
3.peek函数: 稍稍改动一下poll函数即可，poll函数是弹出栈，peek只需要返回stack2的栈顶即可;

4.isEmpty:当两个栈同时为空，才可以判断队列为空；

---

2.3.最小栈

class MinStack {
    private Stack<Integer> stack1;
    private Stack<Integer> MinStack;

    public MinStack() {
        stack1 = new Stack<>();
        MinStack = new Stack<>();
    }

    public void push(int val) {
        stack1.push(val);
        if(MinStack.empty()) {
            MinStack.push(val);
        } else {
            if(val <= MinStack.peek()) {
                MinStack.push(val);
            }
        }
    }
    //题目规定了栈不为空，所以这里没判断
    public void pop() {
        int tmp = stack1.pop();
        if(tmp == MinStack.peek()) {
            MinStack.pop();
        }
    }
    //题目规定了栈不为空
    public int top() {
        return stack1.peek();
    }

    public int getMin() {
        return MinStack.peek();
    }
}

题目的目的是想让我们在O(1)时间复杂度内拿到栈的最小值，所以这里我们不能去遍历栈，而是需要用到两个栈，下面用画图的形式分析一下如何做到：

 谢谢观看！！！