反向传播
当神经网络层数很多,每一层又有很多神经元时,参数就异常的多,我们为了实现梯度下降,就要求L(参数1,参数2...)对所有参数的微分,,假如有一百万个参数,每次梯度下降就要求100万次微分,这个计算量可想而知

反向传播就是为了解决在求损失函数对参数的微分计算量太大的问题,基于链式法则,我们先回顾一下链式法则
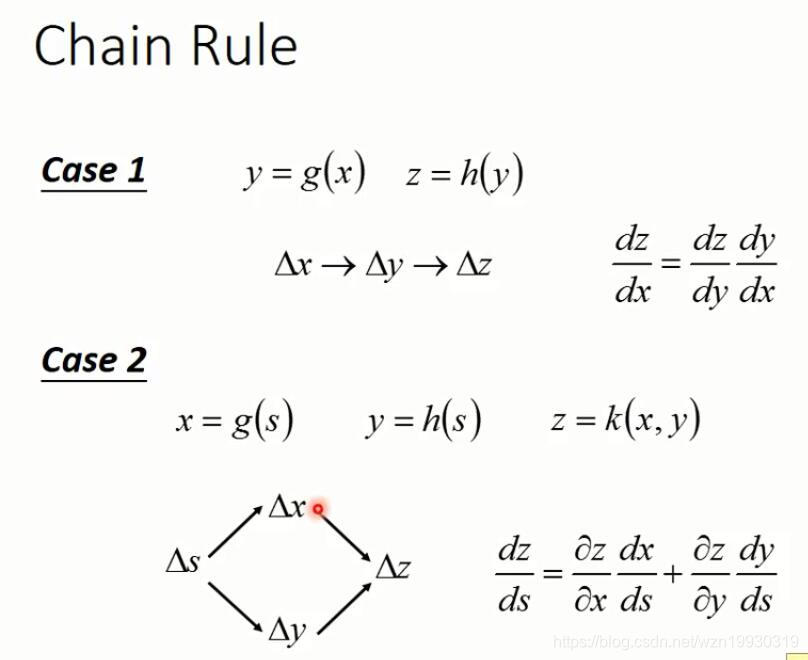
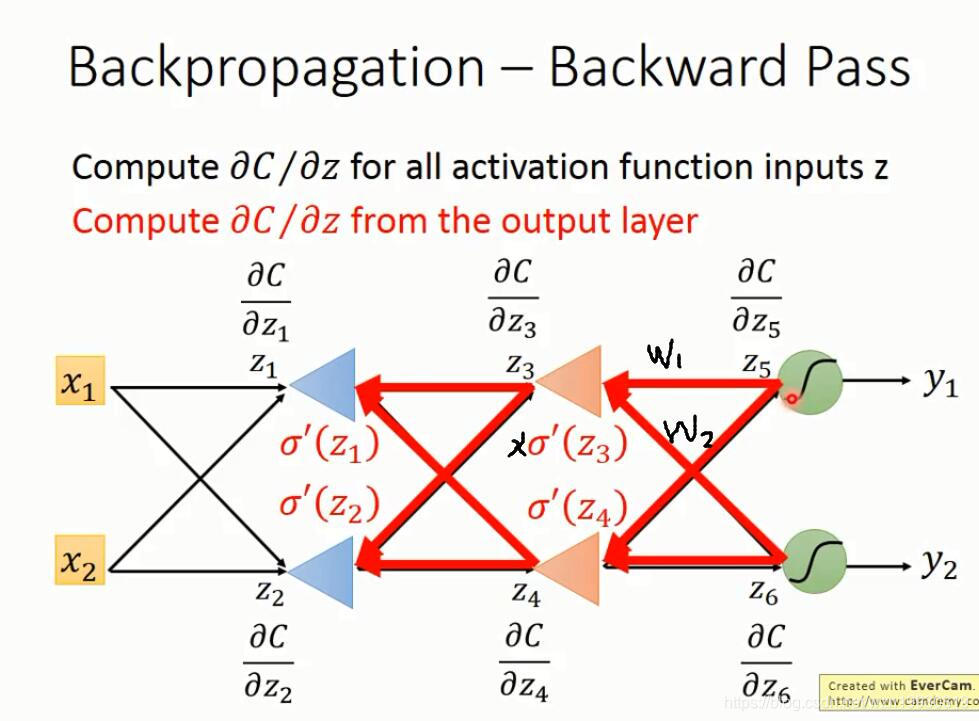
下面就是反向传播的计算过程
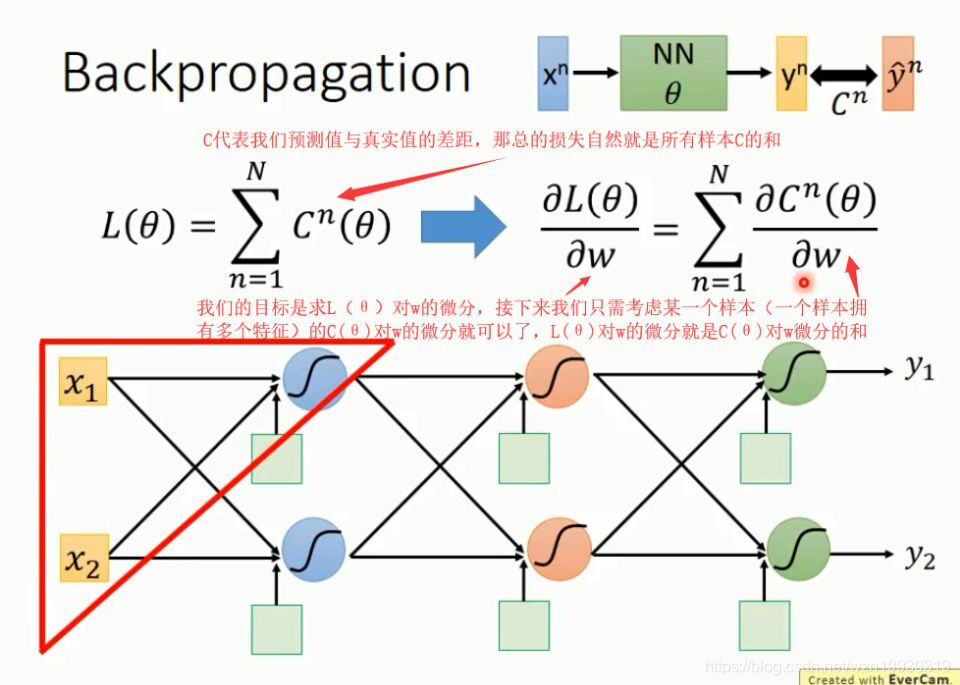
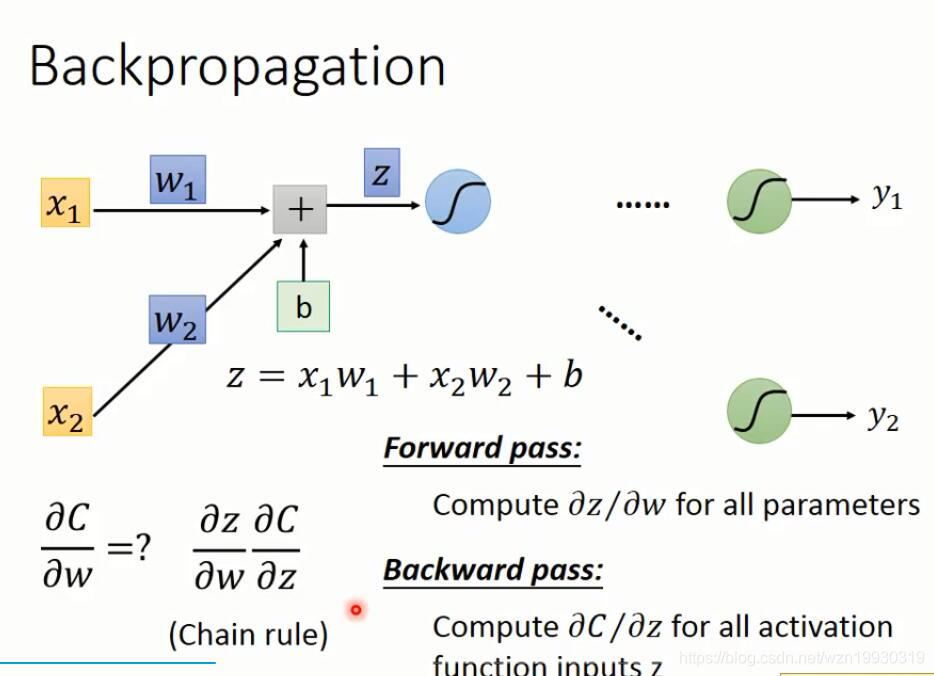
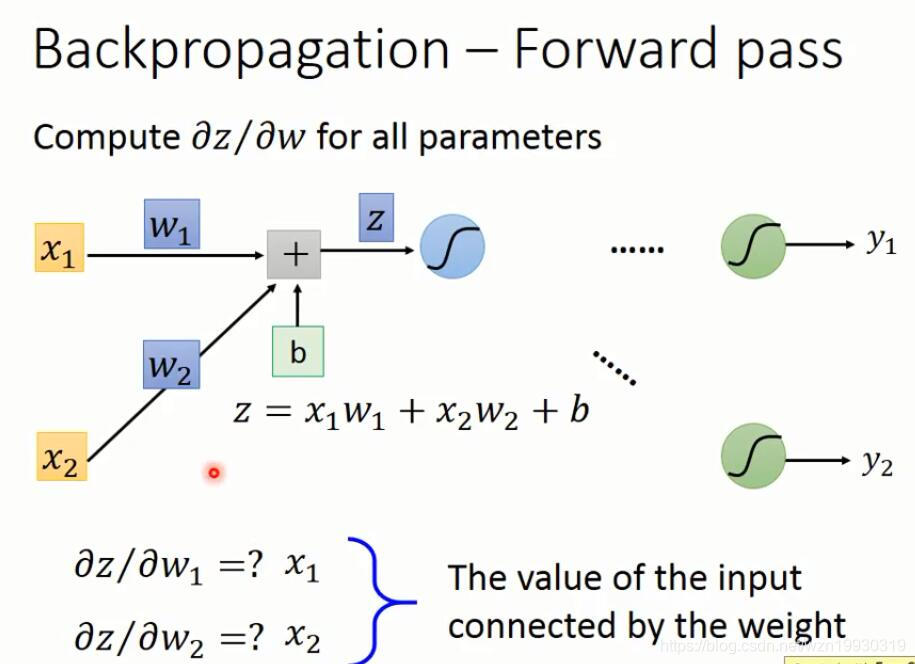
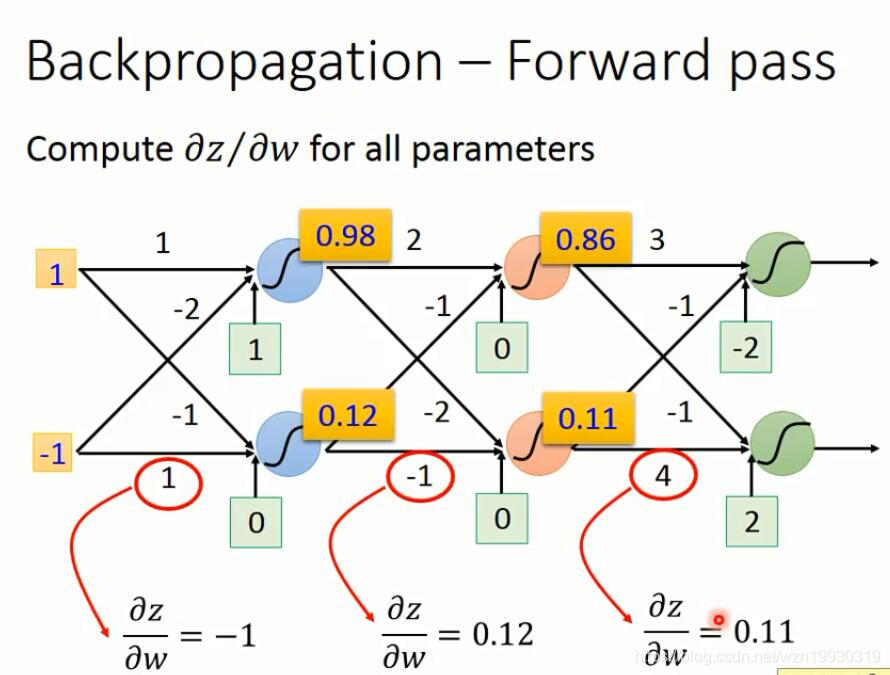
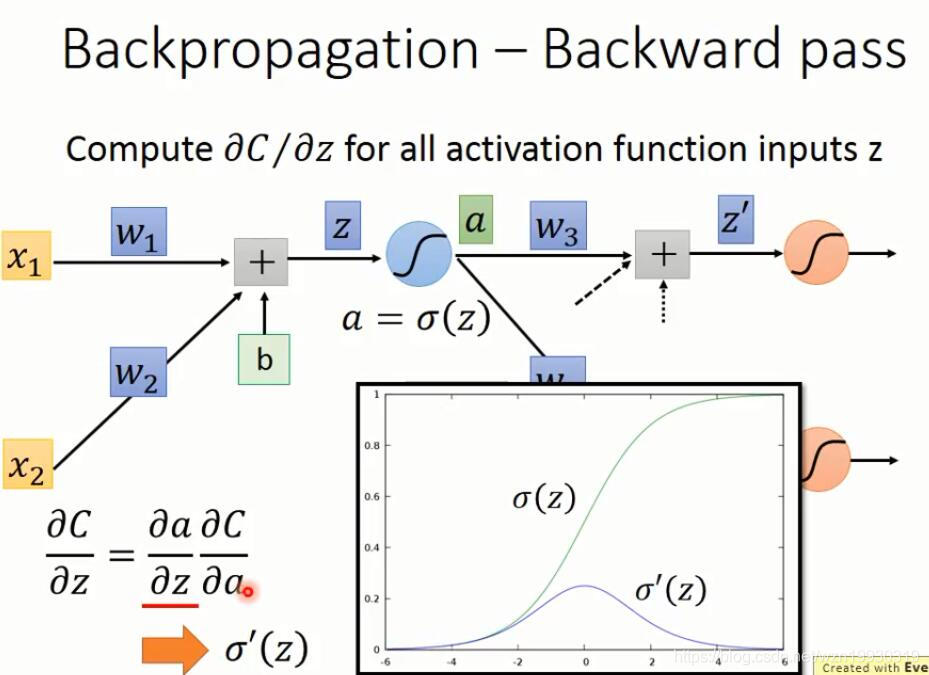
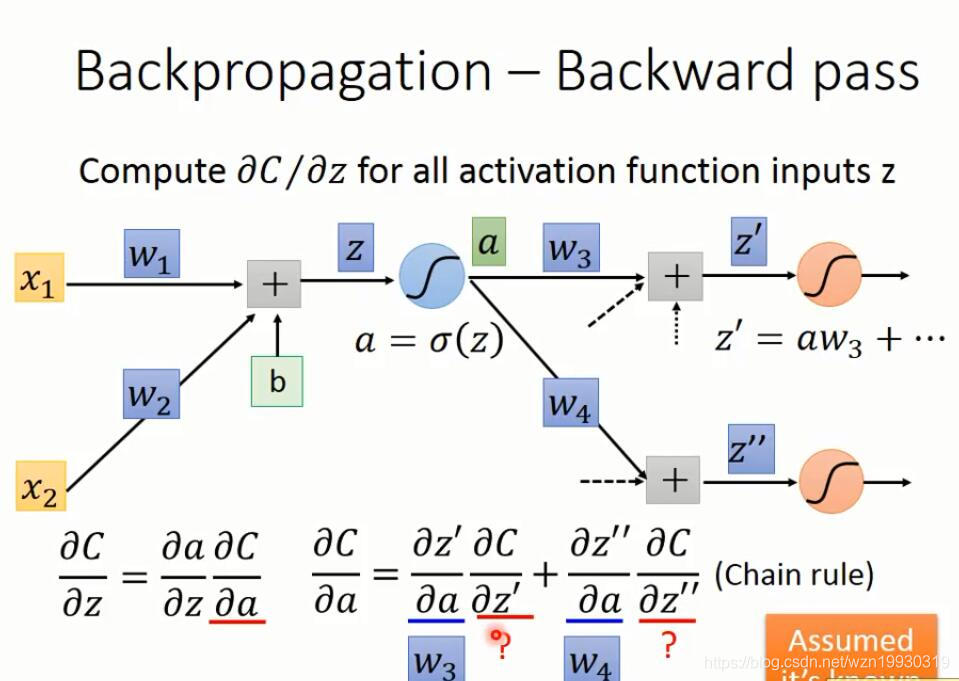
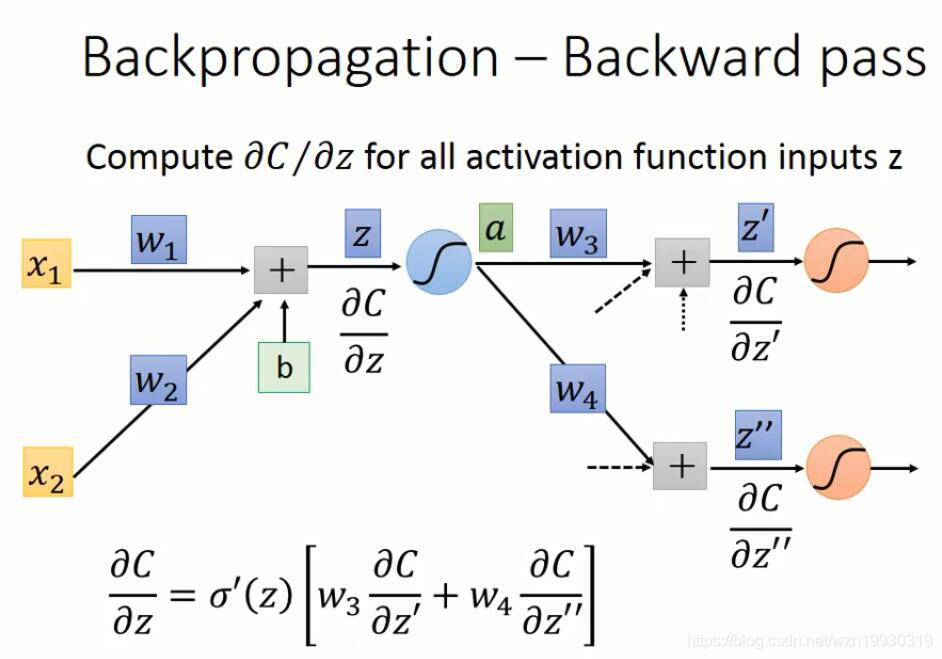
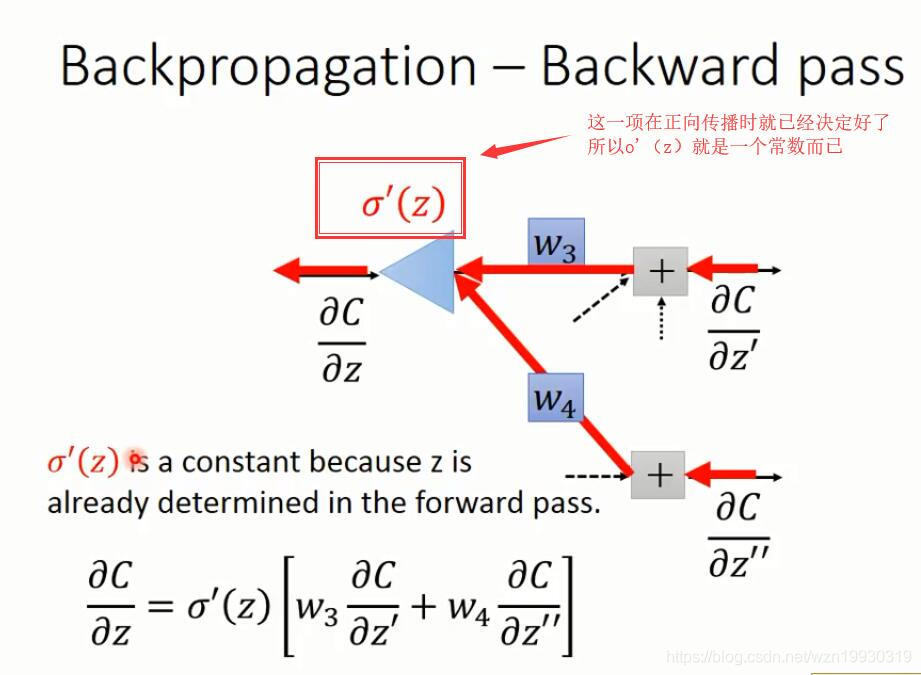
上面的dC/dz,看过Ng的课应该知道,这就是Ng定义的δ
(#^.^#)
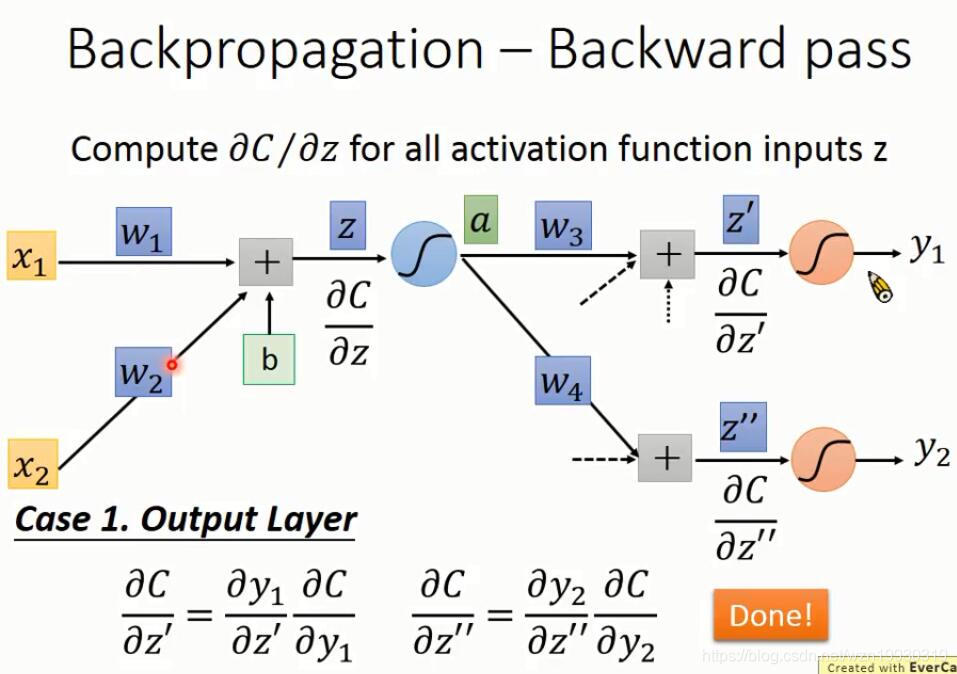
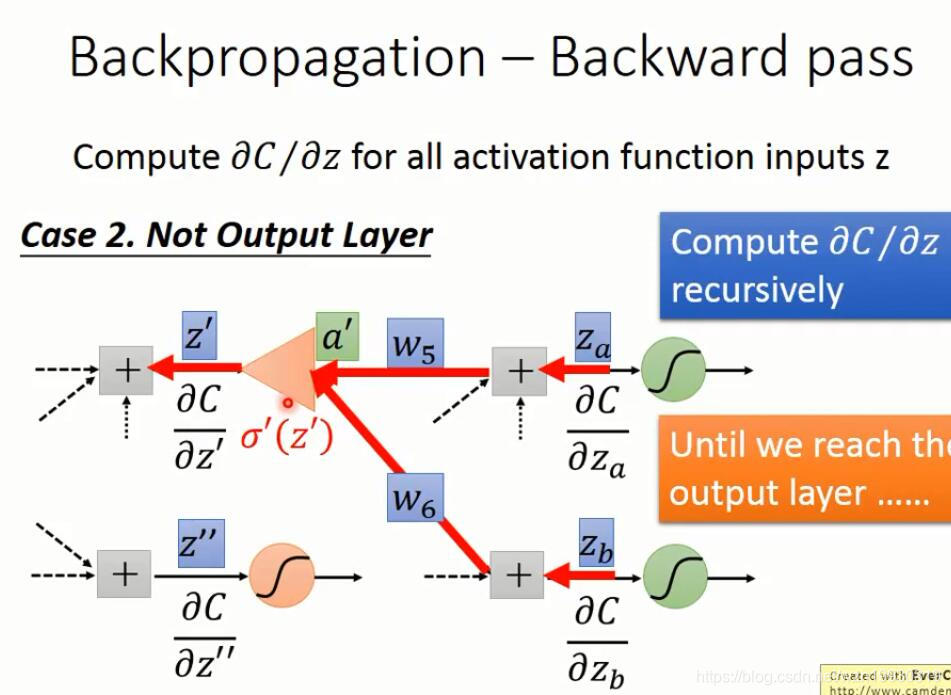
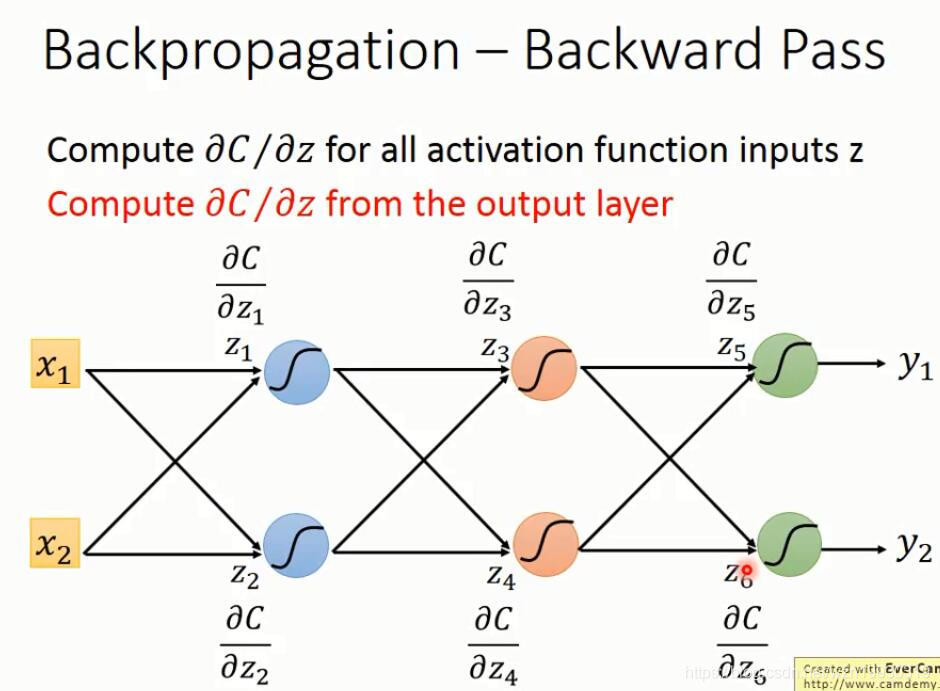
 本文深入探讨了神经网络中反向传播算法的核心概念,解释了如何通过链式法则解决大量参数的梯度计算问题,旨在帮助读者理解深度学习中梯度下降的高效实现。
本文深入探讨了神经网络中反向传播算法的核心概念,解释了如何通过链式法则解决大量参数的梯度计算问题,旨在帮助读者理解深度学习中梯度下降的高效实现。
当神经网络层数很多,每一层又有很多神经元时,参数就异常的多,我们为了实现梯度下降,就要求L(参数1,参数2...)对所有参数的微分,,假如有一百万个参数,每次梯度下降就要求100万次微分,这个计算量可想而知

反向传播就是为了解决在求损失函数对参数的微分计算量太大的问题,基于链式法则,我们先回顾一下链式法则

下面就是反向传播的计算过程








上面的dC/dz,看过Ng的课应该知道,这就是Ng定义的δ
(#^.^#)




 2190
2190

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


