渐次全局网络裁剪 (总结7)

1.1 网络裁剪的一般过程

        网络裁剪通常遵循“筛选-裁剪-微调”三步。 “筛选”指的是根据一定的准则,选择出待裁剪的目标,通常被筛选出的裁减目标是对网络性能影响较小的对象,或者是冗余的对象。筛选出待裁剪对象后,进行第二步裁剪。我们通过把与神经元相连的所有参数置为0,或者将滤波器的所有参数置为0来进行裁剪。此时,在物理上神经元仍然存在于网络之中,但在信号处理的流程里,参数被置0的神经元已经不能对网络的运算做出任何贡献,在信号处理流程中被裁剪出了网络。一般而言,进行网络裁减后,网络的性能会退化。性能退化的主要原因是网络裁剪导致网络参数脱出了之前的局部最优点,因此需要进行微调。

        如果网络的裁剪是通过参数置0的方法完成的,那么在微调的时候需要注意阻止这些参数更新。如果网络的裁剪是物理上将目标脱出网络,则可以直接进行微调。将网络提升到原有性能所需要的微调次数是衡量网络裁剪效果的重要指标之一。

1.2 神经元贡献评价

        在这里我们将卷积层中的一个滤波器或全连接层中的一个计算节点统称为神经元。在神经元级的网络裁剪中,神经元的重要性评价,或称为神经元贡献评价是网络裁剪的核心问题。神经元贡献评价就是为网络中的每一个神经元打一个分数,该贡献分反应了当前神经元对网络性能的影响情况。通常,对网络性能贡献度较小的神经元会被最先剪除。一种简单的评价神经元贡献的方法是,观察剪除该神经元后网络在验证集上的性能变化,并以此作为神经元的得分。这种评价方式相对而言最为有效,但深度神经网络通常含有成千上万个神经元,而神经元的贡献分在每一轮裁剪和微调后又需要重新评估,因此这种打分方式是极为低效的。

1.3 数据相关的评价准则

        我们将文献[75]对神经连接的贡献评价推广到神经元上。由于该类评价准则的神经元分数贡献需要借助训练集,因此我们称之为为数据相关的评价准则。首先,我们规定网络层对数据的响应。我们记Y l 为卷积层对单个输入样本的输出,则Y l ∈ R m×n×c ,该层卷积层对输入样本的响应定义为样本在该层的输出特征沿通道维的平均。这种定义方式实际上取的是滤波器对该样本响应的强度,等价于在卷积层后的全局平均值池化。对全连接网络而言,网络的计算节点对样本的响应是单个实数值,因此全连阶层的输出可以直接作为网络对样本的响应。不含有参数的网络层不是网络裁剪的对象,因此不必规定。设第l层网络对第i个训练样本的响应为R i l ,训练集样本数为N ,则我们可以利用神经元对训练集响应的平均值作为神经元贡献准则,定义如下:

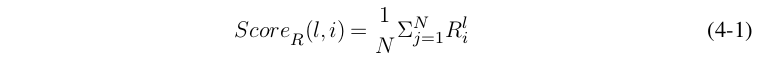
R评价方法的基本思想是,神经元对样本的响应强度决定了它对样本的敏感度。如果一个神经元对整个训练集的样本的响应都不高,那么它对神经网络而言是不重要的,因为它无法产生具有影响力的输出。
        另一种基于一阶统计量的贡献度评分标准是标准差分数σ(R),其神经元贡献分定义如式(4-2)。

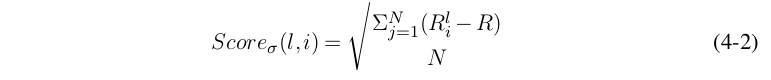
σ(R)评价方法的基本思想是,如果神经元对整个训练集的所有样本都具有稳定的响应,则该神经元所提取的特征不具有判别性,不能以之为分类依据。因此该神经元对网络而言是冗余的。值得注意的是,在全连接网络中,依据σ(R)指标裁剪神经元时,应当通过神经连接将该神经元的平均响应传递到后序神经元中,作为偏置的调整项。

[75] G. Thimm, E. Fiesler. Evaluating pruning methods[J]. Proceedings of International Symposium on Artificial Neural Networks, 1995, 2:20–25

1.4 数据无关的评价准则

        数据相关的评价准则适合于在迁移学习中评估原网络对新样本空间的响应情况,但数据相关评价准则的缺点是计算量相对较大,为了得到神经元分数,我们必须得到网络各层在训练集上的全部输出。
        数据无关的评价准则使用的则是网络本身的性质,此类方法计算量小,特别适合于从初始化参数针对具体任务训练而成的网络的裁剪。在这里我们介绍的数据无关评价准则称为平均权值绝对值和(Average Absolute Weight Sum, AAWS),该评价方法在文献 [49] 提出,我们对它进行进一步推广以使其适应全连接网络。对卷积核而言,其定义如式(4-3)。

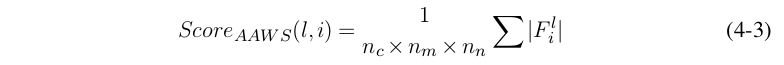
[49] H. Li, A. Kadav, I. Durdanovic, et al. Pruning Filters for Efficient ConvNets[J]. arXiv preprint arXiv:1608.08710, 2017

其中,n c × n m × n n 是卷积核中含有的参数总数,|F i l |则是第l层的第i个卷积核。对全连接层而言,我们定义一个神经元的AAWS分数为起于该神经元的所有连接权重之和,由于全连接的参数有矩阵表达,因此全连接的AAWS分数可定义如式(4-4)。其中,W 为全连接网络的权重参数,n为全连阶层的输出维度。

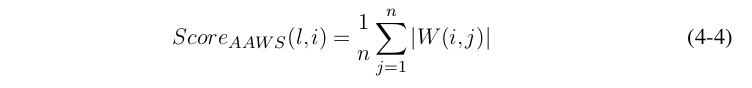
数据无关的评价准则不需要在每一步裁减过程中获得网络各个层的响应信息,因此计算速度较快。但在迁移学习的场景下,由于原始网络的权重不能反映新训练集的信息,数据无关的评价准则不能够正确评估神经元的重要情况。我们将在下一节通过实验证明。

1.5 层间神经元贡献偏差与消除

       目前，神经元的裁剪采用的是逐层裁剪。逐层裁剪的“筛选-裁剪-微调”以层为单位进行，每个裁剪循环只针对一层神经元进行裁剪和微调。逐层裁剪的优点在于能够通过多轮微调使网络逐渐适应新的输入分布，对网络性能影响较小。逐层裁剪的缺点主要有二，一是所需要的微调次数很多，二是我们无法确定应该在每层裁减掉多少神经元。因此，在本节中，我们考虑构建全局的裁减方案。
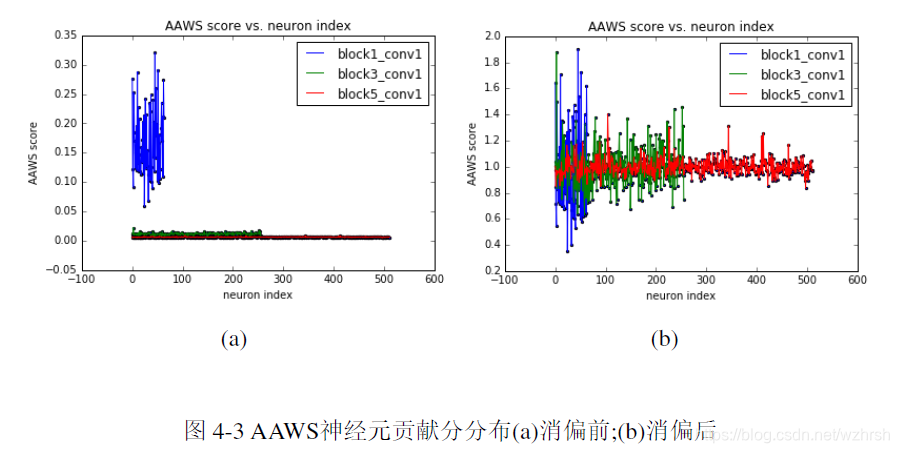
       全局裁剪的方案是在每一轮裁剪中，将所有的神经元的贡献统一评估，随后在全网络范围内筛选对网络性能影响最小的神经元进行裁剪，最后对全网络微调。全局的裁减方案具有自适应性强，运算消耗少等优点。然而，上节提到的神经元贡献度评价指标无法直接应用于全局裁剪，因为不同层级之间的贡献分存在系统性偏差。图4-1(a)、图4-2(a)是我们在实验阶段训练的网络一些层的?和?(?)贡献分分布情况。可以看到网络倾向于对底层的神经元给出较低的分，而对高层神经元给出较高的分数，不同层的神经元得分存在显著的系统性偏差。之所以我们认定这些分数不能反应神经元的真实贡献，是因为如果按照图中所示的得分分布进行裁剪，则网络的近输入端层将被首先被全部裁剪，而没有底层网络对数据特征的低级提取，网络就无从进行模式推断。图4-3(a)是VGG-16网络若干层的AAWS得分，它对高层倾向于给出低分，而对底层给出高分。

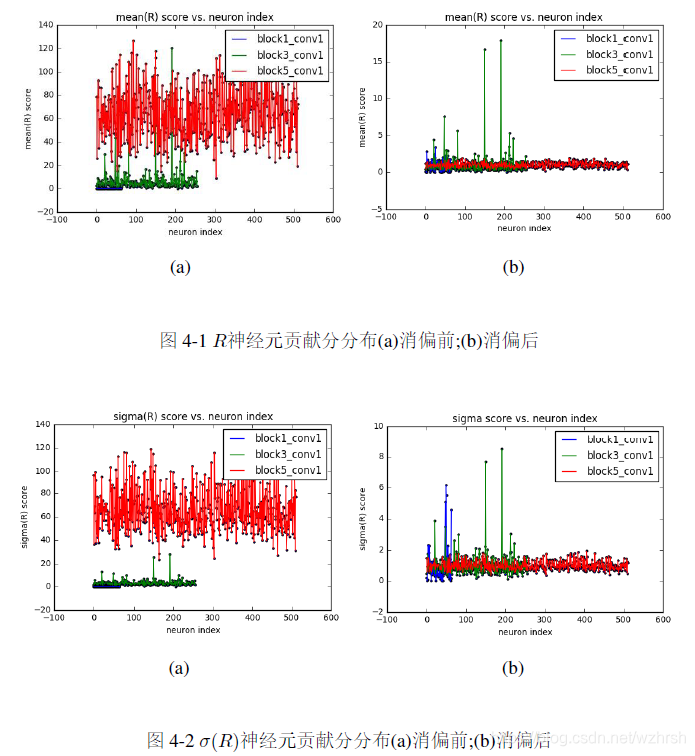
为了实现全局网络裁剪，我们需要对层间神经元贡献偏差进行消除。在我们的框架中，我们简单的将各层神经元得分除以该层神经元得分的均值进行贡献分消偏，经过调整的分数如式，其中??是该层的神经元总数。

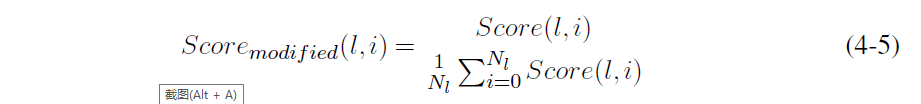
经过消偏后，不同评分方法得到的网络神经元得分分布分别如图图4-1(b)、图4-2(b)和图4-3(b)可以看到，各个层的得分被比较均匀的混合在一起，且同一层内得分的差异性也得到保持。另一种在全局裁剪与逐层裁剪间折中的方案我们称为全局等比例裁剪。这种裁剪方案在每轮裁剪中等比例的在各层筛选出冗余神经元。全局等比例裁剪大大减少了逐层裁剪所需的计算量，但其假设是，网络的冗余神经元等比例的分布在各个层之间。后面我们将通过实验证明这种假设并不正确。

1.6 渐次全局网络裁剪框架

       我们将所提出的渐次全局网络裁剪框架总结如算法2。
       我们称该算法是全局的，因为冗余神经元的筛选在整个网络中进行，而不是在某一层网络进行。我们称该算法是渐次的，是因为在这个框架中每一步裁剪都只选取一小部分神经元。全局的裁剪能够大大降低网络裁剪所需要的微调次数，渐次裁剪能够保证网络参数点的位置尽可能保持在原局部最优点处，使得通过少数几轮微调即可使网络恢复因网络裁剪而下降的性能。

       渐次网络裁剪的另一个优点是，我们无需再规定各个层在一轮裁剪中所需要裁减掉的神经元数目。在给定的网络性能指标下，该框架可以通过反复的全局筛选、裁剪、微调来自动的逐渐逼近网络的最优结构。我们称渐次网络裁剪具有能够自动发现给定性能指标下网络的近似最有结构的能力。通过渐次全局网络裁剪的框架，我们可以用每次裁剪的步长来控制裁剪到合适结构时所需要的循环次数。裁剪步长越大，则越能够快速逼近目标网络结构。裁剪步长越小，逼近目标网络结构需要的循环次数会变多，但得到的网络结构会更加精细。

1.7 算法设计与实现

       我们将介绍对所提出渐次全局裁剪框架的代码实现，我们使用开源深度学习框架Keras实现了上节中提出的算法，并在若干神经网络上进行实验。

实验设计与结果将在后文中介绍，代码设计的原则是为神经元级的网络裁剪提供统一框架。
       我们的渐次全局裁减算法仍然遵循了先筛选，再裁剪，最后微调的三步裁剪方案。算法的代码实现遵循了模块化的思想，即筛选、裁剪、微调三个部分应尽量减少耦合。为了兼容不同冗余神经元遴选算法和不同的裁剪策略，我们设计了一个名为“NetScore”的类，将筛选和裁剪的过程解耦。我们规定每个神经元的贡献分是由“层名”，“神经元下标”和“神经元得分”构成的三元元组。“NetScore”对象只负责读入符合要求的数据，并按照给定的裁剪模式和比例返回筛选得到的冗余神经元，而不干涉神经元评分和裁剪的具体过程。同样，神经元评分的代码只需要给出符合要求的三元组数据即可。

       通过“NetScore”的解耦，我们可以实现任意的神经元评分方法和任意的神经元裁剪方法。在本文的实验中，我们逐层逐神经元进行评分，并将评分结果读入“NetScore”对象。随后，我们按照指定的筛选模式从“NetScore”中获取冗余神经元的信息，并逐个执行裁剪操作。
       我们通过将与冗余神经元相连的所有连接置为0，使神经元在信号处理流程中脱出网络，达到裁剪的目的。需要注意的是，在含有BN层的网络中，需要在裁剪对应神经元的同时，对该神经元对应的BN计算结点进行修正。具体而言，BN层为每个神经元配置了均值?(?)，方差? ??(?)，再放缩参数?和?，在裁剪中，我们应设置?(?) = 0，? = 0，? = 0，并设? ??(?) = 1，以避免BN层干扰计算。
       完成神经元筛选和裁剪后，我们将从原网络中抽取出未被裁剪到的神经元构成子网络，所得到的子网络就是在该步裁剪后得到的模型。子网络抽取保留原网络中所有参数不全为0的神经元和它们的连接关系。值得注意的是，对卷积网络而言，其输出特征图的尺寸与该层中滤波器数目相关，当我们删除一层的若干滤波器时，应当同时调整下一层神经网络滤波器的卷积核形状。具体而言，设某层卷积层输出特征图为? ∈ ??×?×?，则紧邻其后的卷积层滤波器形状为? ∈??1×?2×?。记? = {?1,?2, . . .??}是该卷积层将被删除的滤波器，则经过删除后，卷积层的输出尺寸为? ∈ ??×?×(?−|?|)，为了保证网络的正常运行，紧邻其后的卷积层中滤波器也应调整为? ∈ ??1×?2×(?−|?|)，其中被删除的|?|个通道的下标为{?1,?2, . . .??}。
        此外，对栈式网络结构而言，当网络从卷积层向全连接层过度时，需要利用Flatten层将卷积层的输出向量化。为了抽取子网络，需要确定经过Flatten后得到的一维向量中需要保留的计算结点位置。在本文的实现中，我们通过生成一个“虚假”的卷积层输出特征图，将保留的卷积核对应的特征图设为1，将删除的卷积核对应的特征图设为0。当这个虚假的特征图经过Flatten向量化后，值为1的点即为需要保留的计算结点。
       抽取得到的子网络将使用标准的训练和测试方法进行微调和性能评估，经过微调的网络可以作为模型检查点保存。

       小结：我们从几种面向神经连接的贡献度评价指标中推广出用于神经元裁剪的评价指标，并指出这些指标存在的层间得分系统性偏差问题。我们用简单的方式消除层间偏差，并基于此提出渐近全局裁剪方法，从原理上说明渐近全局裁剪方法的优势。最后，我们介绍了算法在代码实现层面上所采用的方法和技巧。