线性选择的C++实现

元素选择问题的一般提法：

给定线性序集中n个元素和整个k，1<=k<=n,要求找出这n个元素中的第k小的元素，如果将这n个元素依其线性序排列时，排在第k个元素即为要找的元素。
k=1时，找到最小元素。
k=n时，找到最大元素。
k=(n+1)/2时，找中位数。

1. 一般选择问题的分治算法
   基本思想对输入数组进行递归划分。
   与快速排序不同的是，它只对划分出的子数组之一进行递归处理。

2. 线性时间选择核心代码
   int Partition(int a[], int low, int high)
   {
   int i = low, j = high + 1;
   int x = a[low];
   while (true)
   {
   //将<x的元素交换到左边区域
   while (a[++i] < x && i < high);
   //将>x的元素交换到右边区域
   while (a[–j] > x);

   if (i >= j) break;
   Swap(a[i], a[j]);
   }
   a[low] = a[j];
   a[j] = x;
   return j;
   }
   int Random(int low, int high) {//随机找到一个位置
   return (rand() % (high - low + 1)) + low;
   }

int RandomizedPartition(int a[], int low, int high)//根据位置划分
{
int i = Random(low, high);//在新的分区里找到新的随机基准点
Swap(a[i], a[low]);//将随机基准点和第一个位置交换
return Partition(a, low, high);//后面的分区以第一个元素为基准 重新区分
}
int RandomizedSelect(int a[], int low, int high, int k)
{
if (low == high)
return a[low];//找到当前所需的位置，返回当前值。
int i = RandomizedPartition(a, low, high);//重新区分，找到新分区里的基准点传给i
int j = i - low + 1;//小组的个数
if (k <= j)//重新区分后，根据基准元素返回索引，考虑下面往哪里寻找
return RandomizedSelect(a, low, i, k);
else
return RandomizedSelect(a, i + 1, high, k - j);
}

4. 优化
   select类似于前面的randomizedSelect算法，但是可以在O(n)时间内。
   如果在线性时间内找到一个划分基准，使得划分这个
   基准所划分出的两个子数组的长度都至少为原数组长度的ᵋ倍（0<ᵋ<1）。
   举个例子：若ᵋ=9/10，算法递归调用所产生的子数组的长度至少缩短1/10。在最坏的情况，算法所需要时间T(n)<=T(9n/10)+O(n)。由此可得T(n)=O(n).

5. 优化线性时间选择核心代码
   int select(int a[], int p, int r, int k)
   {
   if (r - p<75)//n<75时计算时间不超过一个常数C1
   {
   //用某个简单排序算法对数组a[p:r]排序
   quicksort(a, p, r);
   return a[p + k - 1];
   }
   else//n>=75时递归调用
   {
   //将a[p+5i]至a[p+5i+4]的第3小元素 与a[p+i]交换位置；
   for (int i = 0; i <= (r - p - 4) / 5; i++)
   //共执行n/5次，每次需要O(1)时间 所以for循环需要O(n)时间
   {
   quicksort(a, p + 5 * i, p + 5 * i + 4);
   swap(a[p + 5 * i + 2], a[p + i]);
   }
   //递归调用select
   int x = select(a, p, p + (r - p - 4) / 5, (r - p - 4) / 10);//找到中位数x后
   int i = partition(a, p, r, x);//以x为基准调用partition对数组a[p:r]重新区分，找到新分区里的基准点传给i(这需要O(n)时间)
   int j = i - p + 1;//小组的个数
   if (k <= j)//重新区分后，根据基准元素返回索引，考虑下面往哪里寻找
   return select(a, p, i, k);
   else return select(a, i + 1, r, k - j);
   }
   }

6. 时间复杂度：
   设对n个元素的数组调用算法select，需要
   T（n）时间，那么找中位数x至多用T（n/5）的时间。
   按照算法所选的基准x进行划分所得到的2个子数组分别至多有3n/4个元素。所以无论对哪一个子数组调用select都至多用了T(3n/4)的时间。

7. T(n)的递归式为：
   
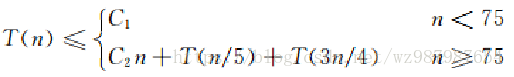
   解此递归式可得：T(n)=O(n)