最大互信息系数

对最大互信息系数的一些思考

最大互信息系数（MIC）

MIC（Maximal Information Coefficient）最大互信息系数。用来衡量两个特征变量之间的关联程度（线性或非线性关系），相较于Mutual Information（MI）互信息而言有更高的准确度。其主要思想是：如果两个变量之间存在一定的相关性，那么在这两个变量的散点图上进行某种网格划分之后，根据这两个变量在网格中的近似概率密度分布，可计算这两个变量的互信息，正则化后，该值可用于衡量这两个变量之间的相关性
MIC 基本原理会利用到互信息概念，互信息的概念使用以下方程来说明：

MIC的想法是针对两个变量之间的关系离散在二维空间中，并且使用散点图来表示，将当前二维空间在 x,y 方向分别划分为一定的区间数，然后查看当前的散点在各个方格中落入的情况，这就是联合概率的计算，这样就解决了在互信息中的联合概率难求的问题。下面是MIC的计算公式：

上式中 a,b 是在 x,y 方向上的划分格子的个数，本质上就是网格分布，B 是变量，在原作者的论文中提到 B 的大小设置是数据量的 0.6 次方左右。
算法的通俗理解：
MIC计算分为三个步骤：

1. 给定i、j，对X、Y构成的散点图进行i列j行网格化，并求出最大的互信息值
2. 对最大的互信息值进行归一化
3. 选择不同尺度下互信息的最大值作为MIC值

最大互信息的求取与数据自身的分布有关系？

在对变量之间的非线性相关性进行分析时，发现有的变量其自身的最大互信息系数都不为1。因此，画出这几个变量与其他几个互信息系数为1的变量进行比较。

求最大的互信息系数时，首先需要对给定的X、Y的散点图进行网格化，再求不同网格化方案下的互信息值，找到最大互信息值。这样，由于碳目标值分布具有离散性，而网格化的过程又具有随机性，从而导致最大互信息不为1。
人造了2000个数据点，分布如下图，其分布如下，可看出这些数据点虽然离散但是分布较为均匀，计算得到的最大信息系数为1。

from minepy import MINE
import numpy as np
A=np.zeros(2000)
A[0:200]=1
A[200:500]=1.5
A[500:700]=1.6
A[700:900]=1.7
A[900:1000]=2
A[1000:1200]=2.5
A[1200:1400]=3
A[1400:1500]=3.2
A[1500:1800]=3.1
A[1800:2000]=3.4
mine = MINE(alpha=0.6, c=15)
mine.compute_score(A,A)
S=mine.mic()

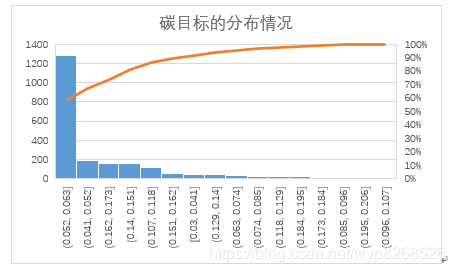
根据碳目标值的分布情况，如下图所示，发现碳目标值的分布具有明显的偏态现象

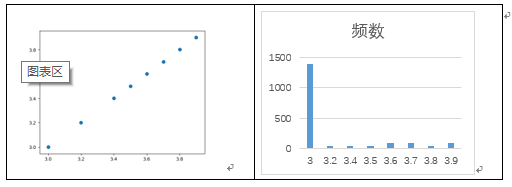
接下来，人造一组具有类似分布的数据（如下图所示），计算其最大信息系数为0.88

from minepy import MINE
import numpy as np
B=np.zeros(2000)
B[0:1400]=3
B[1400:1450]=3.2
B[1451:1600]=3.4
B[1600:1650]=3.5
B[1650:1750]=3.6
B[1750:1850]=3.7
B[1850:1900]=3.8
B[1900:2000]=3.9
mine = MINE(alpha=0.6, c=15)
mine.compute_score(A,B)
S=mine.mic()

因此得出结论（不知正确与否）：当数据具有离散性且偏态分布式，数据自身的最大信息系数可能出现不为1的现象。