题目3
为下列的正则表达式构造最少状态DFA:
(1)(a|b)*a(a|b)
e -> a|b
![![[Blank diagram (4).png|400]]](https://i-blog.csdnimg.cn/direct/277a262d38f04f148d5b280e86fa43dc.png)
e -> (a|b)*
![![[Blank diagram (11).png|1000]]](https://i-blog.csdnimg.cn/direct/fc1e4c8cf78e41e58a006b884b2f39e8.png)
e -> (a|b)*a(a|b)
![![[Blank diagram (15).png|666]]](https://i-blog.csdnimg.cn/direct/30cabbd32f764f4cb92bb15551a80129.png)
利用子集构造算法将NFA转为DFA:
初始状态:{s0}:q0{q0}→ε{s0,s1,s2,s4,s7,s8}:q0{q0}→a{s3,s9}→ε{s1,s2,s3,s4,s6,s7,s8,s9,s10,s11,s13}:q1{q0}→b{s5}→ε{s1,s2,s4,s5,s6,s7,s8}:q2{q1}→a{s3,s9,s12}→ε{s1,s2,s3,s4,s6,s7,s8,s9,s10,s11,s12,s13,s15}:q3{q1}→b{s5,s14}→ε{s1,s2,s4,s5,s6,s7,s8,s14,s15}:q4{q2}→a{s3,s9}→ε{s1,s2,s3,s4,s6,s7,s8,s9,s10,s11,s13}:q1{q2}→b{s5}→ε{s1,s2,s4,s5,s6,s7,s8}:q2{q3}→a{s3,s9,s12}→ε{s1,s2,s3,s4,s6,s7,s8,s9,s10,s11,s12,s13,s15}:q3{q3}→b{s5,s14}→ε{s1,s2,s4,s5,s6,s7,s8,s14,s15}:q4{q4}→a{s3,s9}→ε{s1,s2,s3,s4,s6,s7,s8,s9,s10,s11,s13}:q1{q4}→b{s5}→ε{s1,s2,s4,s5,s6,s7,s8}:q2
\begin{aligned}
&初始状态:\{s_0\}:q_0\\
&\{q_0\}\xrightarrow{ε}\{s_0, s_1, s_2, s_4, s_7, s_8\}:q_0\\
&\{q_0\}\xrightarrow{a}\{s_3, s_9\}\xrightarrow{ε}\{s_1, s_2, s_3, s_4, s_6, s_7, s_8, s_9, s_{10}, s_{11}, s_{13}\}:q_1\\
&\{q_0\}\xrightarrow{b}\{s_5\}\xrightarrow{ε}\{s_1, s_2, s_4, s_5, s_6, s_7, s_8\}:q_2\\
&\{q_1\}\xrightarrow{a}\{s_3, s_9, s_{12}\}\xrightarrow{ε}\{s_1, s_2, s_3, s_4, s_6, s_7, s_8, s_9, s_{10}, s_{11}, s_{12}, s_{13}, s_{15}\}:q_3\\
&\{q_1\}\xrightarrow{b}\{s_5, s_{14}\}\xrightarrow{ε}\{s_1, s_2, s_4, s_5, s_6, s_7, s_8, s_{14}, s_{15}\}:q_4\\
&\{q_2\}\xrightarrow{a}\{s_3, s_9\}\xrightarrow{ε}\{s_1, s_2, s_3, s_4, s_6, s_7, s_8, s_9, s_{10}, s_{11}, s_{13}\}:q_1\\
&\{q_2\}\xrightarrow{b}\{s_5\}\xrightarrow{ε}\{s_1, s_2, s_4, s_5, s_6, s_7, s_8\}:q_2\\
&\{q_3\}\xrightarrow{a}\{s_3, s_9, s_{12}\}\xrightarrow{ε}\{s_1, s_2, s_3, s_4, s_6, s_7, s_8, s_9, s_{10}, s_{11}, s_{12}, s_{13}, s_{15}\}:q_3\\
&\{q_3\}\xrightarrow{b}\{s_5, s_{14}\}\xrightarrow{ε}\{s_1, s_2, s_4, s_5, s_6, s_7, s_8, s_{14}, s_{15}\}:q_4\\
&\{q_4\}\xrightarrow{a}\{s_3, s_9\}\xrightarrow{ε}\{s_1, s_2, s_3, s_4, s_6, s_7, s_8, s_9, s_{10}, s_{11}, s_{13}\}:q_1\\
&\{q_4\}\xrightarrow{b}\{s_5\}\xrightarrow{ε}\{s_1, s_2, s_4, s_5, s_6, s_7, s_8\}:q_2\\
\end{aligned}
初始状态:{s0}:q0{q0}ε{s0,s1,s2,s4,s7,s8}:q0{q0}a{s3,s9}ε{s1,s2,s3,s4,s6,s7,s8,s9,s10,s11,s13}:q1{q0}b{s5}ε{s1,s2,s4,s5,s6,s7,s8}:q2{q1}a{s3,s9,s12}ε{s1,s2,s3,s4,s6,s7,s8,s9,s10,s11,s12,s13,s15}:q3{q1}b{s5,s14}ε{s1,s2,s4,s5,s6,s7,s8,s14,s15}:q4{q2}a{s3,s9}ε{s1,s2,s3,s4,s6,s7,s8,s9,s10,s11,s13}:q1{q2}b{s5}ε{s1,s2,s4,s5,s6,s7,s8}:q2{q3}a{s3,s9,s12}ε{s1,s2,s3,s4,s6,s7,s8,s9,s10,s11,s12,s13,s15}:q3{q3}b{s5,s14}ε{s1,s2,s4,s5,s6,s7,s8,s14,s15}:q4{q4}a{s3,s9}ε{s1,s2,s3,s4,s6,s7,s8,s9,s10,s11,s13}:q1{q4}b{s5}ε{s1,s2,s4,s5,s6,s7,s8}:q2
![![[Blank diagram (29).png]]](https://i-blog.csdnimg.cn/direct/e4d3ab86ded94a539674f91cdf654dd3.png)
将DFA简化到最小:
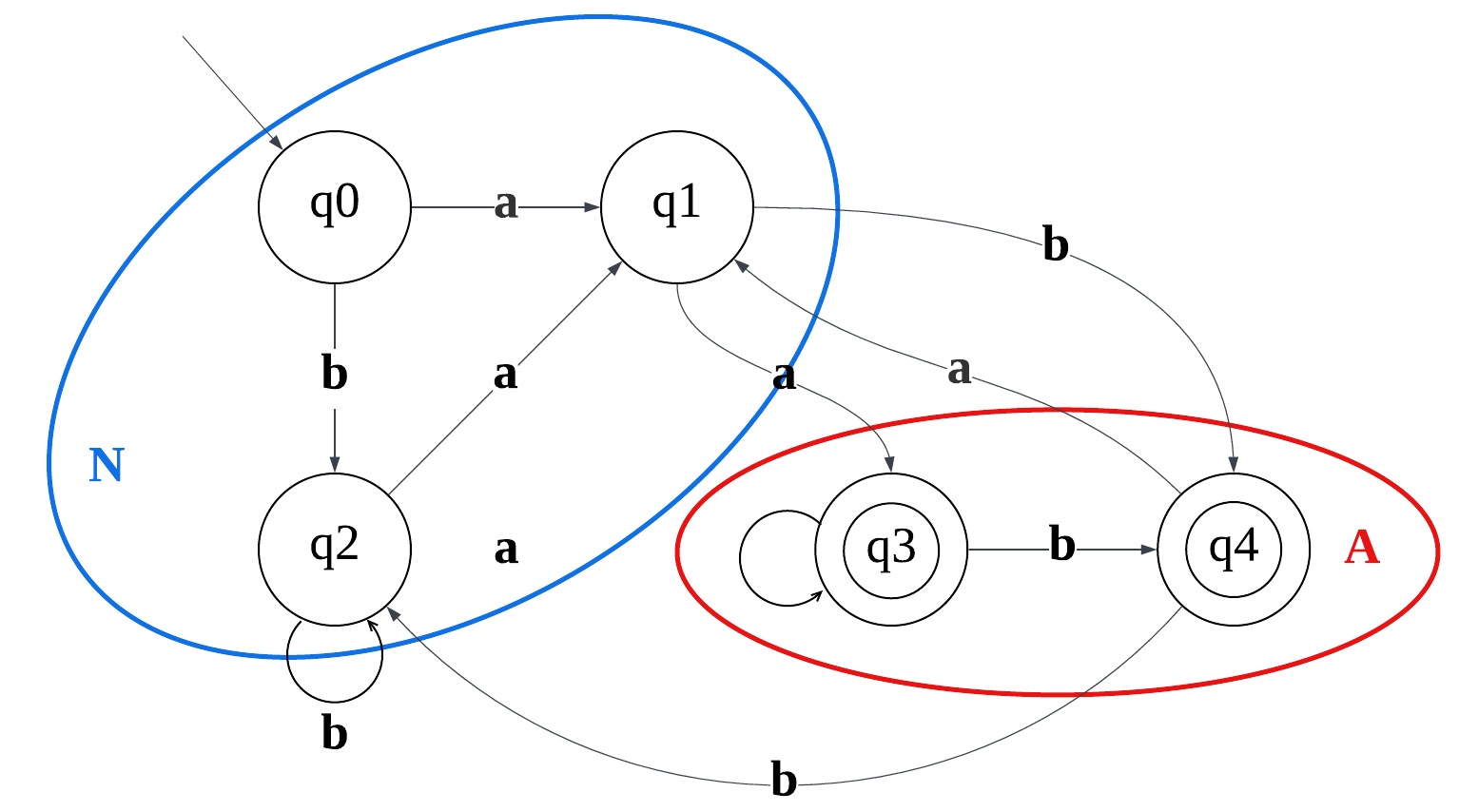
字符a可以分裂DFA,对于N中状态:δ(q0,a)=q1∈Nδ(q1,a)=q3∉Nδ(q2,a)=q1∈N对于A中状态:δ(q3,a)=q3∈Aδ(q4,a)=q1∉A因此字符a可将原DFA分裂为{q0,q2},{q1},{q3},{q4}此后字符b和a都不能继续分裂DFA,因此最简的DFA:
\begin{aligned}
&字符a可以分裂DFA,对于N中状态:\\
&δ(q_0,a)=q_1 \in N \\
&δ(q_1,a)=q_3 \notin N \\
&δ(q_2,a)=q_1 \in N \\
&对于A中状态:\\
&δ(q_3,a)=q_3 \in A \\
&δ(q_4,a)=q_1 \notin A \\
&因此字符a可将原DFA分裂为\{q_0, q_2\}, \{q_1\}, \{q_3\}, \{q_4\}\\
&此后字符b和a都不能继续分裂DFA,因此最简的DFA:
\end{aligned}
字符a可以分裂DFA,对于N中状态:δ(q0,a)=q1∈Nδ(q1,a)=q3∈/Nδ(q2,a)=q1∈N对于A中状态:δ(q3,a)=q3∈Aδ(q4,a)=q1∈/A因此字符a可将原DFA分裂为{q0,q2},{q1},{q3},{q4}此后字符b和a都不能继续分裂DFA,因此最简的DFA:
![![[Blank diagram (28).png]]](https://i-blog.csdnimg.cn/direct/f80d82bf83bd4551b4db48e95d430847.png)
(2)(a|b)*a(a|b)(a|b)
e -> (a|b)*a(a|b)(a|b)
![![[Blank diagram (19) 1.png]]](https://i-blog.csdnimg.cn/direct/6e73413d1875433597a41879d2344c02.png)
利用子集构造算法将NFA转为DFA:
初始状态:{s0}:q0{q0}→ε{s0,s1,s2,s4,s7,s8}:q0{q0}→a{s3,s9}→ε{s1,s2,s3,s4,s6,s7,s8,s9,s10,s11,s13}:q1{q0}→b{s5}→ε{s1,s2,s4,s5,s6,s7,s8}:q2{q1}→a{s3,s9,s12}→ε{s1,s2,s3,s4,s6,s7,s8,s9,s10,s11,s12,s13,s15,s16,s17,s19}:q3{q1}→b{s5,s14}→ε{s1,s2,s4,s5,s6,s7,s8,s14,s15,s16,s17,s19}:q4{q2}→a{s3,s9}→ε{s1,s2,s3,s4,s6,s7,s8,s9,s10,s11,s13}:q1{q2}→b{s5}→ε{s1,s2,s4,s5,s6,s7,s8}:q2{q3}→a{s3,s9,s12,s18}→ε{s1,s2,s3,s4,s6,s7,s8,s9,s10,s11,s12,s13,s15,s16,s17,s18,s19,s21}:q5{q3}→b{s5,s14,s20}→ε{s1,s2,s4,s5,s6,s7,s8,s14,s15,s16,s17,s19,s20,s21}:q6{q4}→a{s3,s9,s18}→ε{s1,s2,s3,s4,s6,s7,s8,s9,s10,s11,s13,s18,s21}:q7{q4}→b{s5,s20}→ε{s1,s2,s4,s5,s6,s7,s8,s20,s21}:q8{q5}→a{s3,s9,s12,s18}→ε{s1,s2,s3,s4,s6,s7,s8,s9,s10,s11,s12,s13,s15,s16,s17,s18,s19,s21}:q5{q5}→b{s5,s14,s20}→ε{s1,s2,s4,s5,s6,s7,s8,s14,s15,s16,s17,s19,s20,s21}:q6{q6}→a{s3,s9,s18}→ε{s1,s2,s3,s4,s6,s7,s8,s9,s10,s11,s13,s18,s21}:q7{q6}→b{s5,s14,s20}→ε{s1,s2,s4,s5,s6,s7,s8,s20,s21}:q8{q7}→a{s3,s9,s12}→ε{s1,s2,s3,s4,s6,s7,s8,s9,s10,s11,s12,s13,s15,s16,s17,s19}:q3{q7}→b{s5,s14}→ε{s1,s2,s4,s5,s6,s7,s8,s14,s15,s16,s17,s19}:q4{q8}→a{s3,s9}→ε{s1,s2,s3,s4,s6,s7,s8,s9,s10,s11,s13}:q1{q8}→b{s5}→ε{s1,s2,s4,s5,s6,s7,s8}:q2
\begin{aligned}
&初始状态:\{s_0\}:q_0\\
&\{q_0\}\xrightarrow{ε}\{s_0, s_1, s_2, s_4, s_7, s_8\}:q_0\\
&\{q_0\}\xrightarrow{a}\{s_3, s_9\}\xrightarrow{ε}\{s_1, s_2, s_3, s_4, s_6, s_7, s_8, s_9, s_{10}, s_{11}, s_{13}\}:q_1\\
&\{q_0\}\xrightarrow{b}\{s_5\}\xrightarrow{ε}\{s_1, s_2, s_4, s_5, s_6, s_7, s_8\}:q_2\\
&\{q_1\}\xrightarrow{a}\{s_3, s_9, s_{12}\}\xrightarrow{ε}\{s_1, s_2, s_3, s_4, s_6, s_7, s_8, s_9, s_{10}, s_{11}, s_{12}, s_{13}, s_{15}, s_{16}, s_{17}, s_{19}\}:q_3\\
&\{q_1\}\xrightarrow{b}\{s_5, s_{14}\}\xrightarrow{ε}\{s_1, s_2, s_4, s_5, s_6, s_7, s_8, s_{14}, s_{15}, s_{16}, s_{17}, s_{19}\}:q_4\\
&\{q_2\}\xrightarrow{a}\{s_3, s_9\}\xrightarrow{ε}\{s_1, s_2, s_3, s_4, s_6, s_7, s_8, s_9, s_{10}, s_{11}, s_{13}\}:q_1\\
&\{q_2\}\xrightarrow{b}\{s_5\}\xrightarrow{ε}\{s_1, s_2, s_4, s_5, s_6, s_7, s_8\}:q_2\\
&\{q_3\}\xrightarrow{a}\{s_3, s_9, s_{12}, s_{18}\}\xrightarrow{ε}\{s_1, s_2, s_3, s_4, s_6, s_7, s_8, s_9, s_{10}, s_{11}, s_{12}, s_{13}, s_{15}, s_{16}, s_{17}, s_{18}, s_{19}, s_{21}\}:q_5\\
&\{q_3\}\xrightarrow{b}\{s_5, s_{14}, s_{20}\}\xrightarrow{ε}\{s_1, s_2, s_4, s_5, s_6, s_7, s_8, s_{14}, s_{15}, s_{16}, s_{17}, s_{19}, s_{20}, s_{21}\}:q_6\\
&\{q_4\}\xrightarrow{a}\{s_3, s_9, s_{18}\}\xrightarrow{ε}\{s_1, s_2, s_3, s_4, s_6, s_7, s_8, s_9, s_{10}, s_{11}, s_{13}, s_{18}, s_{21}\}:q_7\\
&\{q_4\}\xrightarrow{b}\{s_5, s_{20}\}\xrightarrow{ε}\{s_1, s_2, s_4, s_5, s_6, s_7, s_8, s_{20}, s_{21}\}:q_8\\
&\{q_5\}\xrightarrow{a}\{s_3, s_9, s_{12}, s_{18}\}\xrightarrow{ε}\{s_1, s_2, s_3, s_4, s_6, s_7, s_8, s_9, s_{10}, s_{11}, s_{12}, s_{13}, s_{15}, s_{16}, s_{17}, s_{18}, s_{19}, s_{21}\}:q_5\\
&\{q_5\}\xrightarrow{b}\{s_5, s_{14}, s_{20}\}\xrightarrow{ε}\{s_1, s_2, s_4, s_5, s_6, s_7, s_8, s_{14}, s_{15}, s_{16}, s_{17}, s_{19}, s_{20}, s_{21}\}:q_6\\
&\{q_6\}\xrightarrow{a}\{s_3, s_9, s_{18}\}\xrightarrow{ε}\{s_1, s_2, s_3, s_4, s_6, s_7, s_8, s_9, s_{10}, s_{11}, s_{13}, s_{18}, s_{21}\}:q_7\\
&\{q_6\}\xrightarrow{b}\{s_5, s_{14}, s_{20}\}\xrightarrow{ε}\{s_1, s_2, s_4, s_5, s_6, s_7, s_8, s_{20}, s_{21}\}:q_8\\
&\{q_7\}\xrightarrow{a}\{s_3, s_9, s_{12}\}\xrightarrow{ε}\{s_1, s_2, s_3, s_4, s_6, s_7, s_8, s_9, s_{10}, s_{11}, s_{12}, s_{13}, s_{15}, s_{16}, s_{17}, s_{19}\}:q_3\\
&\{q_7\}\xrightarrow{b}\{s_5, s_{14}\}\xrightarrow{ε}\{s_1, s_2, s_4, s_5, s_6, s_7, s_8, s_{14}, s_{15}, s_{16}, s_{17}, s_{19}\}: q_4\\
&\{q_8\}\xrightarrow{a}\{s_3, s_9\}\xrightarrow{ε}\{s_1, s_2, s_3, s_4, s_6, s_7, s_8, s_9, s_{10}, s_{11}, s_{13}\}:q_1\\
&\{q_8\}\xrightarrow{b}\{s_5\}\xrightarrow{ε}\{s_1, s_2, s_4, s_5, s_6, s_7, s_8\}:q_2\\
\end{aligned}
初始状态:{s0}:q0{q0}ε{s0,s1,s2,s4,s7,s8}:q0{q0}a{s3,s9}ε{s1,s2,s3,s4,s6,s7,s8,s9,s10,s11,s13}:q1{q0}b{s5}ε{s1,s2,s4,s5,s6,s7,s8}:q2{q1}a{s3,s9,s12}ε{s1,s2,s3,s4,s6,s7,s8,s9,s10,s11,s12,s13,s15,s16,s17,s19}:q3{q1}b{s5,s14}ε{s1,s2,s4,s5,s6,s7,s8,s14,s15,s16,s17,s19}:q4{q2}a{s3,s9}ε{s1,s2,s3,s4,s6,s7,s8,s9,s10,s11,s13}:q1{q2}b{s5}ε{s1,s2,s4,s5,s6,s7,s8}:q2{q3}a{s3,s9,s12,s18}ε{s1,s2,s3,s4,s6,s7,s8,s9,s10,s11,s12,s13,s15,s16,s17,s18,s19,s21}:q5{q3}b{s5,s14,s20}ε{s1,s2,s4,s5,s6,s7,s8,s14,s15,s16,s17,s19,s20,s21}:q6{q4}a{s3,s9,s18}ε{s1,s2,s3,s4,s6,s7,s8,s9,s10,s11,s13,s18,s21}:q7{q4}b{s5,s20}ε{s1,s2,s4,s5,s6,s7,s8,s20,s21}:q8{q5}a{s3,s9,s12,s18}ε{s1,s2,s3,s4,s6,s7,s8,s9,s10,s11,s12,s13,s15,s16,s17,s18,s19,s21}:q5{q5}b{s5,s14,s20}ε{s1,s2,s4,s5,s6,s7,s8,s14,s15,s16,s17,s19,s20,s21}:q6{q6}a{s3,s9,s18}ε{s1,s2,s3,s4,s6,s7,s8,s9,s10,s11,s13,s18,s21}:q7{q6}b{s5,s14,s20}ε{s1,s2,s4,s5,s6,s7,s8,s20,s21}:q8{q7}a{s3,s9,s12}ε{s1,s2,s3,s4,s6,s7,s8,s9,s10,s11,s12,s13,s15,s16,s17,s19}:q3{q7}b{s5,s14}ε{s1,s2,s4,s5,s6,s7,s8,s14,s15,s16,s17,s19}:q4{q8}a{s3,s9}ε{s1,s2,s3,s4,s6,s7,s8,s9,s10,s11,s13}:q1{q8}b{s5}ε{s1,s2,s4,s5,s6,s7,s8}:q2
![![[Blank diagram (21).png|650]]](https://i-blog.csdnimg.cn/direct/a63d67a28a73479f9b18ff9c7956325f.png)
将DFA简化到最小:
![![[Blank diagram (20) 2.png]]](https://i-blog.csdnimg.cn/direct/6c1f5fa07342452daf4d6eb004360a8c.png)
字符a可以分裂DFA,对于N中状态:δ(q0,a)=q1∈Nδ(q1,a)=q3∈Nδ(q2,a)=q1∈Nδ(q3,a)=q5∉Nδ(q4,a)=q7∉N对于A中状态:δ(q5,a)=q5∈Aδ(q6,a)=q7∈Aδ(q7,a)=q3∈Aδ(q8,a)=q1∉A因此字符a可将原DFA分裂为{q0,q1,q2},{q3,q4},{q5,q6},{q7,q8}字符b可以继续分裂DFA,对于N中状态:δ(q0,b)=q2∈{q0,q1,q2}δ(q1,b)=q4∈{q3,q4}δ(q2,b)=q2∈{q0,q1,q2}δ(q3,b)=q6∈{q5,q6}δ(q4,b)=q8∈{q7,q8}对于A中状态:δ(q5,b)=q6∈{q5,q6}δ(q6,b)=q8∈{q7,q8}δ(q7,a)=q4∈{q3,q4}δ(q8,a)=q2∈{q0,q1,q2}因此字符b可将原DFA继续分裂为{q0,q2},{q1},{q3},{q4},{q5},{q6},{q7},{q8}此后字符a和b都不能继续分裂DFA。因此最简的DFA:
\begin{aligned}
&字符a可以分裂DFA,对于N中状态:\\
&δ(q_0,a)=q_1 \in N \\
&δ(q_1,a)=q_3 \in N \\
&δ(q_2,a)=q_1 \in N \\
&δ(q_3,a)=q_5 \notin N \\
&δ(q_4,a)=q_7 \notin N \\
&对于A中状态:\\
&δ(q_5,a)=q_5 \in A \\
&δ(q_6,a)=q_7 \in A \\
&δ(q_7,a)=q_3 \in A \\
&δ(q_8,a)=q_1 \notin A \\
&因此字符a可将原DFA分裂为\{q_0, q_1, q_2\}, \{q_3, q_4\}, \{q_5, q_6\}, \{q_7, q_8\}\\
&字符b可以继续分裂DFA,对于N中状态:\\
&δ(q_0,b)=q_2 \in \{q_0, q_1, q_2\} \\
&δ(q_1,b)=q_4 \in \{q_3, q_4\} \\
&δ(q_2,b)=q_2 \in \{q_0, q_1, q_2\} \\
&δ(q_3,b)=q_6 \in \{q_5, q_6\} \\
&δ(q_4,b)=q_8 \in \{q_7, q_8\} \\
&对于A中状态:\\
&δ(q_5,b)=q_6 \in \{q_5, q_6\} \\
&δ(q_6,b)=q_8 \in \{q_7, q_8\} \\
&δ(q_7,a)=q_4 \in \{q_3, q_4\} \\
&δ(q_8,a)=q_2 \in \{q_0, q_1, q_2\} \\
&因此字符b可将原DFA继续分裂为\{q_0, q_2\}, \{q_1\}, \{q_3\}, \{q_4\}, \{q_5\}, \{q_6\}, \{q_7\}, \{q_8\}\\
&此后字符a和b都不能继续分裂DFA。因此最简的DFA:
\end{aligned}
字符a可以分裂DFA,对于N中状态:δ(q0,a)=q1∈Nδ(q1,a)=q3∈Nδ(q2,a)=q1∈Nδ(q3,a)=q5∈/Nδ(q4,a)=q7∈/N对于A中状态:δ(q5,a)=q5∈Aδ(q6,a)=q7∈Aδ(q7,a)=q3∈Aδ(q8,a)=q1∈/A因此字符a可将原DFA分裂为{q0,q1,q2},{q3,q4},{q5,q6},{q7,q8}字符b可以继续分裂DFA,对于N中状态:δ(q0,b)=q2∈{q0,q1,q2}δ(q1,b)=q4∈{q3,q4}δ(q2,b)=q2∈{q0,q1,q2}δ(q3,b)=q6∈{q5,q6}δ(q4,b)=q8∈{q7,q8}对于A中状态:δ(q5,b)=q6∈{q5,q6}δ(q6,b)=q8∈{q7,q8}δ(q7,a)=q4∈{q3,q4}δ(q8,a)=q2∈{q0,q1,q2}因此字符b可将原DFA继续分裂为{q0,q2},{q1},{q3},{q4},{q5},{q6},{q7},{q8}此后字符a和b都不能继续分裂DFA。因此最简的DFA:
![![[Blank diagram (22).png|650]]](https://i-blog.csdnimg.cn/direct/62748793c08545a38fcc94478b54e968.png)





















 692
692

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








