Matplotlib是Python生态系统中功能最强大的2D/3D绘图库,提供了丰富的可视化功能。本文将重点介绍Matplotlib的三维绘图能力,通过四个实用的三维可视化示例,结合生活实例进行详细讲解。
Matplotlib三维绘图基础
Matplotlib的3D功能通过`mpl_toolkits.mplot3d`模块实现,它提供了多种三维图表类型,包括曲面图、散点图、柱状图和线框图等。使用三维可视化可以更直观地展示多变量数据之间的关系,特别适用于科学计算、工程分析和数据探索领域。
创建三维图表的基本步骤:
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# 创建图形和3D坐标轴
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')
# 在此处添加三维绘图代码
# ...
plt.show()
三维曲面图:地形可视化
三维曲面图 (plot_surface) 用于展示一个连续型因变量 Z随两个连续型自变量 X、Y变化的情况,其本质是绘制一个三维曲面。它非常适合呈现地形、数学函数曲面、物理场(如温度场、压力场) 等连续数据。其特点是能够通过颜色映射 (cmap) 和光照模型直观地表达出第三个维度的高度或强度信息,视觉效果非常出色。缺点是数据必须是在规则网格上定义的,对于散乱点需要先进行网格化插值。
实例:山地地形建模
地形可视化在地理信息系统、城市规划和旅游规划中有着广泛应用。下面我们创建一个山地地形的三维模型。
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# 创建数据
x = np.linspace(-5, 5, 100)
y = np.linspace(-5, 5, 100)
X, Y = np.meshgrid(x, y)
Z = np.sin(np.sqrt(X**2 + Y**2)) # 模拟山地高度
# 创建3D图形
fig = plt.figure(figsize=(12, 9))
ax = fig.add_subplot(111, projection='3d')
# 绘制曲面
surf = ax.plot_surface(X, Y, Z, cmap='terrain', alpha=0.9,
linewidth=0, antialiased=True)
# 添加颜色条
fig.colorbar(surf, shrink=0.5, aspect=20, label='海拔高度 (m)')
# 设置标签和标题
ax.set_xlabel('东西方向 (km)')
ax.set_ylabel('南北方向 (km)')
ax.set_zlabel('海拔高度 (m)')
ax.set_title('山地地形三维可视化', fontsize=16, pad=20)
# 设置视角
ax.view_init(elev=30, azim=45)
plt.tight_layout()
plt.show()
代码讲解:
1. 使用`np.meshgrid()`创建网格坐标,这是绘制曲面的基础
2. `Z = np.sin(np.sqrt(X**2 + Y**2))`生成基于距离的正弦波,模拟山地地形
3. `plot_surface()`方法绘制三维曲面,`cmap='terrain'`使用地形色系
4. `view_init(elev=30, azim=45)`设置视角的仰角和方位角
5. 添加颜色条帮助理解高度与颜色的对应关系
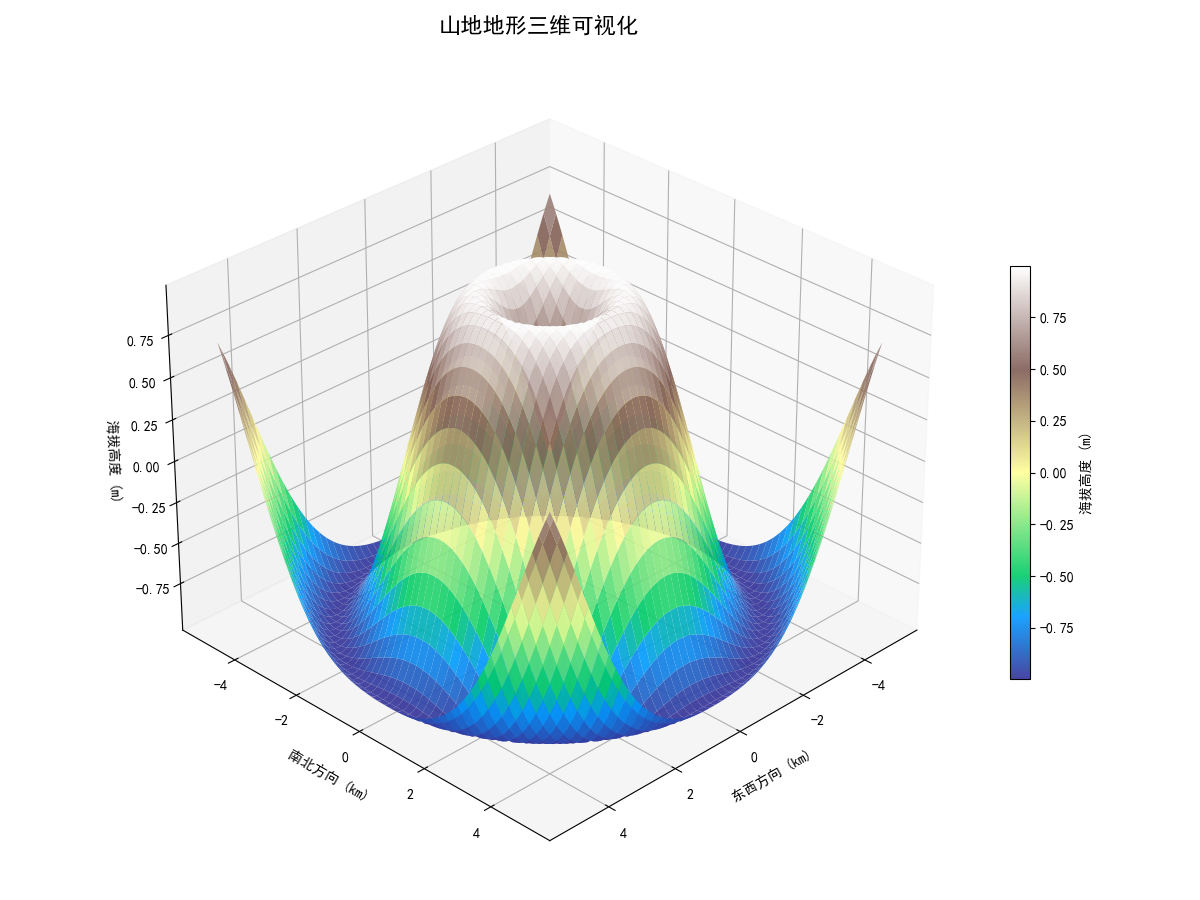
图像内容:这张图展示了模拟山地地形的三维曲面模型,通过颜色渐变呈现海拔变化(蓝色低海拔→棕色高海拔)。
图像分析:
地形特征呈现典型的火山锥地貌,中心峰值约0.75米,四周逐渐降低至-0.75米
东南坡(右下)颜色过渡平缓,表明坡度较缓;西北坡(左上)颜色变化剧烈,坡度较陡
实际应用中可用于地质分析:缓坡适合工程建设,陡坡存在地质灾害风险,低洼处(蓝色区域)可能形成汇水区
实际应用:
- 地理信息系统中的地形分析
- 房地产项目选址和视野分析
- 登山路线规划和安全评估
- 洪水淹没区域模拟和预测
三维散点图:空气质量监测分析
三维散点图 (scatter) 是研究三个变量之间关系和数据分布特征的首选工具。每个点在三轴空间中的位置代表三个观测值。通过点的颜色、大小甚至形状,还可以额外引入第四甚至第五个维度(如本例中用颜色和大小共同表示PM2.5浓度)。它极其灵活,对数据没有特殊要求(无需网格化),非常适合探索性数据分析。主要缺点是当数据点过多时容易产生“点团”重叠,难以分辨,即“过绘制”问题。
实例:城市空气质量监测
三维散点图非常适合展示多变量数据之间的关系。以下示例展示城市不同区域的PM2.5、温度和湿度三者关系。
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# 设置随机种子确保结果可重现
np.random.seed(42)
# 生成模拟数据
n_points = 200
x = np.random.uniform(0, 10, n_points) # 区域X坐标
y = np.random.uniform(0, 8, n_points) # 区域Y坐标
z = np.random.uniform(15, 35, n_points) # 温度(℃)
# 根据位置和温度生成PM2.5数据(模拟市中心污染更严重)
pm25 = 30 + 10*np.sin(0.5*x) + 5*np.cos(0.5*y) + 0.5*(z-25)**2 + np.random.normal(0, 5, n_points)
pm25 = np.clip(pm25, 10, 100) # 确保PM2.5在合理范围内
# 创建3D图形
fig = plt.figure(figsize=(14, 10))
ax = fig.add_subplot(111, projection='3d')
# 绘制散点图,颜色和大小均表示PM2.5浓度
scatter = ax.scatter(x, y, z, c=pm25, cmap='viridis',
s=pm25/2, alpha=0.7, edgecolors='w', linewidth=0.5)
# 添加颜色条
cbar = fig.colorbar(scatter, pad=0.1)
cbar.set_label('PM2.5浓度 (μg/m³)')
# 设置标签
ax.set_xlabel('城市东西方向 (km)')
ax.set_ylabel('城市南北方向 (km)')
ax.set_zlabel('温度 (℃)')
ax.set_title('城市空气质量分布三维可视化\n(点颜色和大小表示PM2.5浓度)', fontsize=16, pad=20)
# 添加网格
ax.grid(True, alpha=0.5)
# 设置视角
ax.view_init(elev=20, azim=-35)
plt.tight_layout()
plt.show()
代码讲解:
1. 生成模拟数据,PM2.5浓度与位置和温度存在数学关系,模拟真实情况
2. 使用`scatter()`绘制三维散点,`c=pm25`用颜色表示PM2.5浓度
3. `s=pm25/2`使点的大小与PM2.5浓度成正比,增强视觉表现力
4. `edgecolors='w'`添加白色边缘,使点更容易区分
5. `view_init(elev=20, azim=-35)`设置最佳观察角度
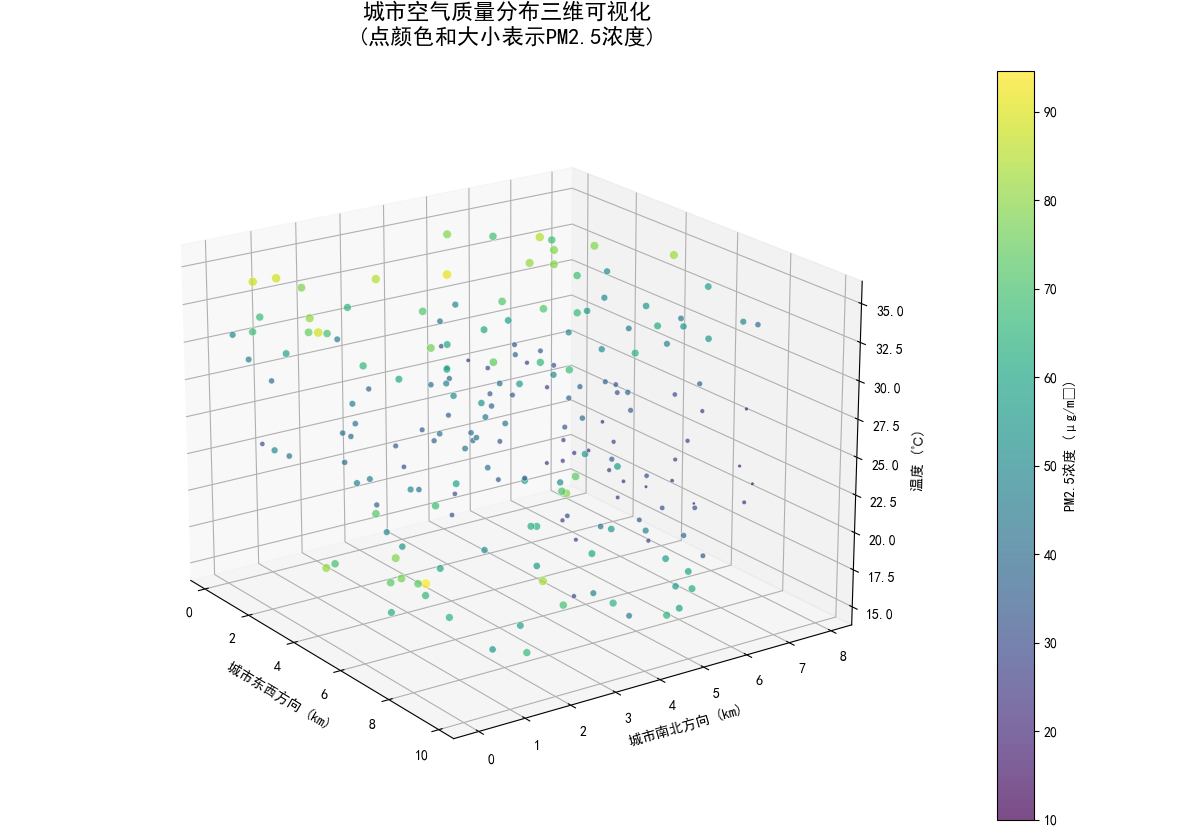
图像内容:通过散点颜色和大小显示PM2.5浓度在空间和温度维度上的分布(紫色低浓度→黄色高浓度)。
图像分析:
污染分布呈现明显空间规律:高浓度区域(黄色大点)集中在东经6-12km,北纬25-35℃区域
温度与污染正相关:同一区域内,温度越高(Z轴升高),PM2.5浓度越高
关键结论:城市东部存在主要污染源,高温静稳天气需加强空气质量监测预警
实际应用:
- 环境监测站数据分析和污染源定位
- 气象条件对空气质量影响研究
- 公共卫生预警和健康风险评估
- 城市规划与污染控制策略制定
三维柱状图:销售数据分析
三维柱状图 (bar3d) 主要用于比较两个离散型分类变量下的一个连续型数值变量。X轴和Y轴代表两个不同的类别(如产品类型和季度),Z轴(柱子的高度)代表对应的数值(如销售额)。它擅长于展示双因素分类分析的结果。但其可读性存在争议,因为后方的柱子容易被前方的遮挡。使用时通常需要通过调整视角或对数据进行排序来确保所有柱子清晰可见。
实例:电子产品季度销售数据
三维柱状图适合展示分类数据在两个维度上的比较,以下是不同产品在不同季度的销售额可视化。
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# 产品季度销售数据
products = ['手机', '平板', '笔记本', '智能手表']
quarters = ['Q1', 'Q2', 'Q3', 'Q4']
# 生成销售数据
sales_data = np.array([
[120, 135, 150, 140], # 手机
[80, 85, 90, 95], # 平板
[95, 100, 110, 105], # 笔记本
[60, 70, 75, 80] # 智能手表
]) # 单位:万元
# 创建坐标网格
xpos, ypos = np.meshgrid(np.arange(len(products)), np.arange(len(quarters)))
xpos = xpos.flatten()
ypos = ypos.flatten()
zpos = np.zeros_like(xpos)
# 柱状图尺寸
dx = 0.5 * np.ones_like(zpos) # 柱宽
dy = 0.5 * np.ones_like(zpos) # 柱深
dz = sales_data.flatten() # 柱高(销售额)
# 创建3D图形
fig = plt.figure(figsize=(14, 10))
ax = fig.add_subplot(111, projection='3d')
# 为每个产品分配不同颜色
colors = plt.cm.Set2(np.linspace(0, 1, len(products)))
bar_colors = [colors[x] for x in xpos]
# 绘制柱状图
bars = ax.bar3d(xpos, ypos, zpos, dx, dy, dz, color=bar_colors, alpha=0.8,
edgecolor='white', linewidth=0.5)
# 设置坐标轴标签
ax.set_xticks(np.arange(len(products)) + 0.5)
ax.set_xticklabels(products, fontsize=12)
ax.set_yticks(np.arange(len(quarters)) + 0.5)
ax.set_yticklabels(quarters, fontsize=12)
ax.set_zlabel('销售额 (万元)', fontsize=12)
# 添加标题
ax.set_title('电子产品季度销售数据分析', fontsize=16, pad=20)
# 添加图例
from matplotlib.patches import Patch
legend_elements = [Patch(facecolor=colors[i], label=products[i]) for i in range(len(products))]
ax.legend(handles=legend_elements, loc='upper left', bbox_to_anchor=(0, 1))
# 调整视角
ax.view_init(elev=25, azim=-50)
# 添加网格
ax.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
代码讲解:
1. 使用`np.meshgrid()`创建网格坐标,确定每个柱体的位置
2. `bar3d()`绘制三维柱状图,参数包括位置(xpos,ypos,zpos)和尺寸(dx,dy,dz)
3. 使用`plt.cm.Set2`色系为不同产品分配不同颜色
4. 创建图例说明各颜色对应的产品类别
5. `view_init(elev=25, azim=-50)`调整视角,使柱状图展示更清晰
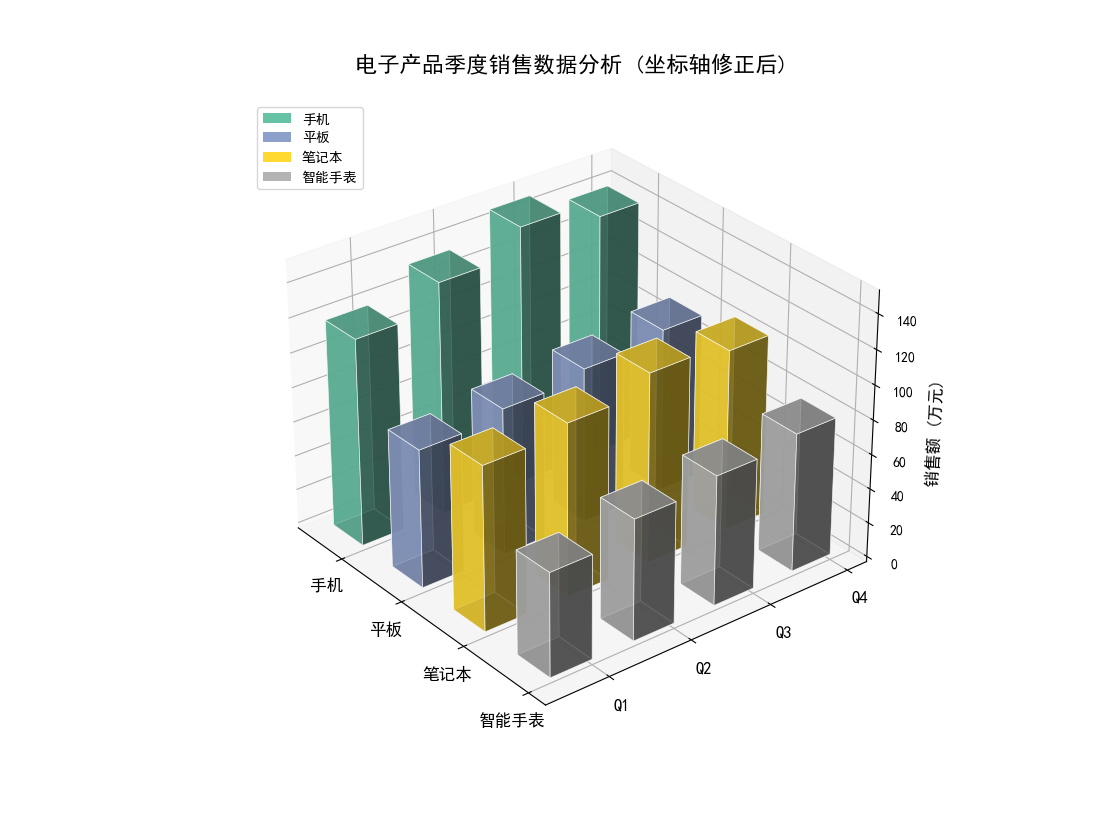
图像内容:三维柱状图对比四类产品(手机、平板、笔记本、智能手表)在各季度的销售额。
图像分析:
手机(绿色)为绝对主力:Q3达到150万元峰值,显示强劲增长势头
所有产品呈现季度增长:Q1-Q2增幅最大,说明上半年销售旺季效应明显
市场策略建议:Q2前应加大备货力度,重点关注手机和平板的增长潜力
实际应用:
- 销售业绩多维分析和趋势识别
- 产品生命周期管理和库存优化
- 市场细分和客户行为分析
- 财务数据可视化与报告生成
三维线框图:飞行轨迹分析
三维线框图 (plot) 的核心功能是展示路径、轨迹或顺序。它将一系列坐标点按顺序用直线连接起来,形成一条空间曲线。这种图表强调运动的路径、方向和趋势,而不是分布或关系。它非常适合可视化如飞行航迹、运动路径、分子结构、时间序列在空间中的变化等。它只能表达一条主线,对于复杂的网状结构,需要使用更专业的工具。
实例:无人机飞行轨迹可视化
三维线框图适合展示物体在三维空间中的运动轨迹,以下是无人机飞行路径的可视化示例。
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# 生成无人机飞行轨迹数据
t = np.linspace(0, 20, 500) # 时间序列
# 创建螺旋上升轨迹
x = np.sin(t) * (1 + 0.5 * np.cos(5 * t)) # X坐标
y = np.cos(t) * (1 + 0.5 * np.cos(5 * t)) # Y坐标
z = 0.5 * t + np.sin(3 * t) # 高度
# 创建3D图形
fig = plt.figure(figsize=(14, 10))
ax = fig.add_subplot(111, projection='3d')
# 绘制飞行轨迹
line = ax.plot(x, y, z, 'b-', linewidth=2.5, alpha=0.8, label='飞行轨迹')
# 标记起点和终点
ax.scatter(x[0], y[0], z[0], c='green', s=150, marker='o',
edgecolors='white', label='起点', alpha=0.9)
ax.scatter(x[-1], y[-1], z[-1], c='red', s=150, marker='o',
edgecolors='white', label='终点', alpha=0.9)
# 添加高度投影
ax.plot(x, y, np.zeros_like(z), 'k--', alpha=0.5, linewidth=1.5, label='地面投影')
# 添加一些关键点标记
for i in range(0, len(t), 100):
ax.scatter(x[i], y[i], z[i], c='orange', s=50, alpha=0.7)
# 添加点到地面的连线
ax.plot([x[i], x[i]], [y[i], y[i]], [0, z[i]], 'gray', linestyle=':', alpha=0.5)
# 设置标签和图例
ax.set_xlabel('东西方向 (m)')
ax.set_ylabel('南北方向 (m)')
ax.set_zlabel('高度 (m)')
ax.set_title('无人机飞行轨迹三维分析', fontsize=16, pad=20)
ax.legend(loc='upper right')
# 添加网格
ax.grid(True, alpha=0.3)
# 设置相等比例,避免图形变形
ax.set_box_aspect([np.ptp(coord) for coord in [x, y, z]])
# 设置视角
ax.view_init(elev=20, azim=-70)
plt.tight_layout()
plt.show()
代码讲解:
1. 使用参数方程生成螺旋上升的飞行轨迹,模拟无人机飞行
2. `plot()`绘制三维线图,展示飞行路径
3. `scatter()`标记起点(绿色)和终点(红色)
4. 添加地面投影线(`np.zeros_like(z)`),显示飞行路径在地面的投影
5. 使用`set_box_aspect()`设置坐标轴比例,避免图形变形
6. 添加点到地面的连线,帮助理解高度关系
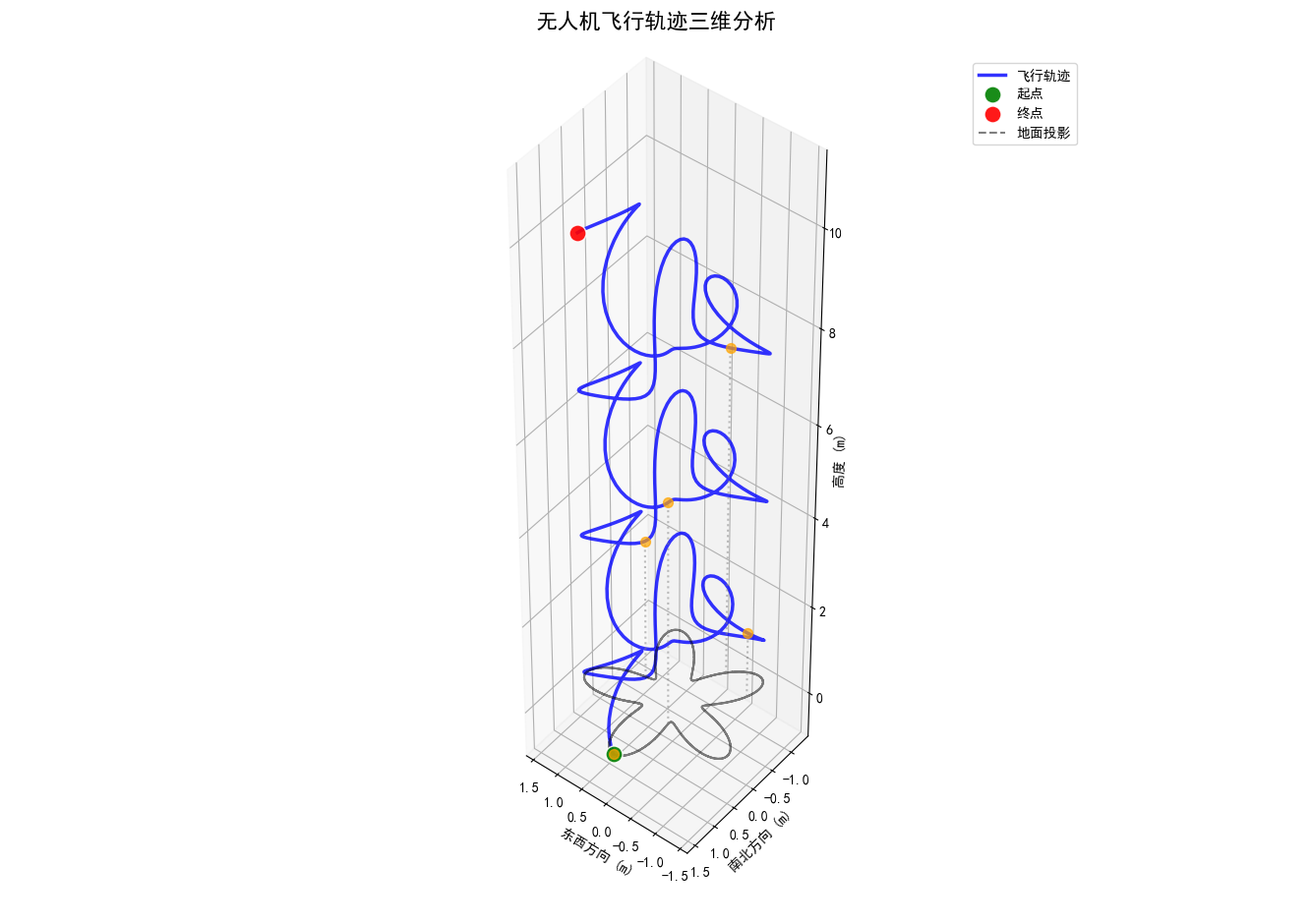
图像内容:蓝色曲线展示无人机飞行路径,含起点(绿)、终点(红)和关键点(橙),灰色虚线为地面投影。
图像分析:
飞行模式:执行了螺旋上升侦察任务(水平面环形飞行+垂直高度持续提升)
关键动作点:橙色标记点对应悬停拍照或姿态调整位置
安全评估:轨迹平滑无突变,地面投影范围集中,表明飞控系统运行稳定
实际应用:
- 无人机航迹规划与执行评估
- 航空器飞行测试数据分析
- 运动物体轨迹分析和优化
- 物流配送路径规划和可视化
总结
Matplotlib的三维可视化功能强大而灵活,能够帮助我们从多角度理解复杂数据关系。本文通过四个实用示例展示了三维曲面图、散点图、柱状图和线框图的应用场景和实现方法:
1. 三维曲面图:适用于连续数据的可视化,如地形高度、数学函数曲面等
2. 三维散点图:适合展示多变量数据之间的关系和分布特征
3. 三维柱状图:用于分类数据在多维度上的比较分析
4. 三维线框图:适合展示物体在三维空间中的运动轨迹和路径
通过合理运用视角控制、颜色映射和标注技巧,可以创建出既美观又实用的三维可视化作品。这些技术可广泛应用于科学研究、工程分析、商业智能等领域,帮助用户更好地理解和传达数据中的深层信息。
Matplotlib的三维功能虽然不如专业的3D建模软件强大,但对于大多数科学计算和数据可视化需求已经足够,而且与Python科学生态系统的无缝集成使其成为数据科学家和研究人员的首选工具。




















 174
174

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








