赫夫曼树及其应用（代码）

在掌握赫夫曼树构建的基础上，实现赫夫曼解码：

一、哈夫曼树的构建满足一下规则：

1.赫夫曼构建中，默认左孩子权值不大于右孩子权值

2.如果遇到两个孩子权值相等，那么按输入顺序或生成顺序来排列。

二、编码规则：

令左孩子分支为编码‘0’，右孩子分支为编码‘1’ 将根结点到叶子结点路径上的分支编码，组合起来，作为该字符的Huffman码。

三、解码：

Huffman是一种前缀编码，解码时不会混淆。任何一个字符的编码都 不是同一字符集中另一个字符的编码的前缀。

四、特点：

利用赫夫曼树可以构造一种不等长的二进制编码，并且构造所得的赫夫曼编码是一种最优前缀编码，即使所传电文的总长度最短。

#include <iostream>
#include <cstring>
using namespace std;

const int MAX = 9999;	   //设定无穷大权值

struct HuffmanNode{
    int weight;//权值
    char c;//字符
    int parent,rchild,lchild;
    char code[MAX];
};

class HuffmanTree{
    HuffmanNode *HT;//节点序列指针
    int num,all_num;
public:
    void selectMin(int i,int &s1,int &s2) //返回当前最小下标
    {   
        s1=0,s2=0;
        for(int j=1;j<=i;j++)
        {
            if(HT[j].parent!=0)
                continue;
            if(s1==0)
                s1=j;
            else if(s2==0)
                s2=j;
            
            if(HT[s1].weight>HT[j].weight)
            {
                s2=s1;
                s1=j;
            }
            else if(s2!=0&&HT[s2].weight>HT[j].weight)
            {
                s2=j;
            }
        }
    }

    void get_HuffmanCode()   //哈夫曼编码de编译
    {  
        for(int i=1;i<=num;i++)
        {
            char code[MAX];
            int a=i,f=HT[a].parent,imag=MAX;
            while(f!=0)
            {
                if(HT[f].lchild==a)
                {
                    code[--imag]='0';
                }
                else if(HT[f].rchild==a)
                {
                    code[--imag]='1';
                }
                a=f;
                f=HT[f].parent;
            }
            cout<<HT[i].weight<<"-";
            for(int h=0;h<MAX-imag;h++)
            {
                HT[i].code[h]=code[MAX-1-h];
                cout<<HT[i].code[h];
            }
            cout<<endl;
        }
    }
    void get_c(char *mi,int ml)
    {
        int q=0,a=all_num;
        string sub="";
        while(1)
        {
            if(q>=ml)
            {
                if(HT[a].c!='\0')
                {
                    sub+=HT[a].c;
                    cout<<sub<<endl;
                }
                else
                {
                    cout<<"error"<<endl;
                }
                return;
            }
            if(HT[a].lchild==0&&HT[a].rchild==0)
            {
                if(HT[a].c=='\0')
                {
                    cout<<"error"<<endl;
                    return;
                }
                sub+=HT[a].c;
                a=all_num;
            }
            if(mi[q]=='0')
                a=HT[a].lchild;
            else if(mi[q]=='1')
                a=HT[a].rchild;
            q++;
        }
    }
    HuffmanTree(){HT=NULL;num=0;all_num=0;}
    HuffmanTree(int hn,char hc[],int hw[])   /***“哈夫曼树”构建***/
    {
        num=hn;
        all_num=2*num-1;
        HT=new HuffmanNode[all_num+1];
        for(int i=1;i<=num;i++)
        {
            HT[i].parent=0;
            HT[i].lchild=0;
            HT[i].rchild=0;
            HT[i].weight=hw[i-1];
            HT[i].c=hc[i-1];
        }
        for(int i=num+1;i<=all_num;i++)
        {
            HT[i].parent=0;
            HT[i].lchild=0;
            HT[i].rchild=0;
            HT[i].weight=0;
            HT[i].c='\0';
        }
        /***开始添加新的子树节点***/
        for(int i=num+1;i<=all_num;i++)
        {
            int s2,s1;//s1<s2 下标
            selectMin(i-1,s1,s2);
            HT[i].weight=HT[s1].weight+HT[s2].weight;
            HT[i].lchild=s1;//下标
            HT[i].rchild=s2;
            HT[s1].parent=i;
            HT[s2].parent=i;
        }
        get_HuffmanCode();//编译
    }
};

int main()
{
    int n,*w;
    char *c;
    cin>>n;
    w=new int[n];
    c=new char[n];
    for(int i=0;i<n;i++)
    {
        cin>>w[i];
    }
    for(int i=0;i<n;i++)
    {
        cin>>c[i];
    }
    HuffmanTree huff(n,c,w);
    cin>>n;
    while (n--)
    {
        char *str;
        cin>>str;
        huff.get_c(str,strlen(str));
    }
    return 0;
}

这里我还另外输出了对应编码的值

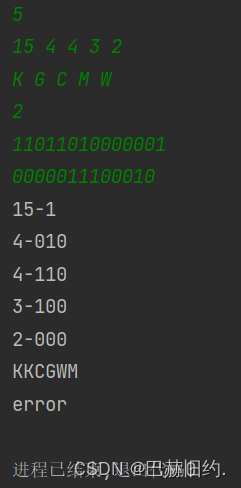
运行结果：                          一点笔记：