哈夫曼树，哈夫曼编码及应用——（代码实现）

最新推荐文章于 2025-09-24 18:50:48 发布

原创

最新推荐文章于 2025-09-24 18:50:48 发布 · 1.7k 阅读

10 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #数据结构

本文详细介绍了哈夫曼树的概念、构造方法及其在数据压缩中的应用。通过实例展示了如何手动和代码实现哈夫曼树的构建，并解释了哈夫曼编码的原理和具体实现，强调了其在提高数据传输效率中的作用。

哈夫曼树，哈夫曼编码及应用

1.哈夫曼树
- 1.1 什么是哈夫曼树
2.如何构造哈夫曼树（哈夫曼算法）
- 2.1 举例实现哈夫曼树
- - 2.1.1手动实现具体步骤
  - 2.1.2代码实现具体步骤
3.哈夫曼编码
- 3.1 什么是哈夫曼编码
- 3.2哈夫曼编码的具体实现
END!!!

1.哈夫曼树

路径长度：从树中一个节点到另一个节点之间的分支构成两个节点之间的路径，路径上的分支数目就成为路径长度。
树的路径长度：从树根到每一节点的路径长度之和。
带权路径长度：考虑到带权的节点，节点的带权路径长度是从该节点到根之间的路径长度与节点权的乘积。
带权路径长度（WPL）：树中所有叶子节点的带权路径长度之和。

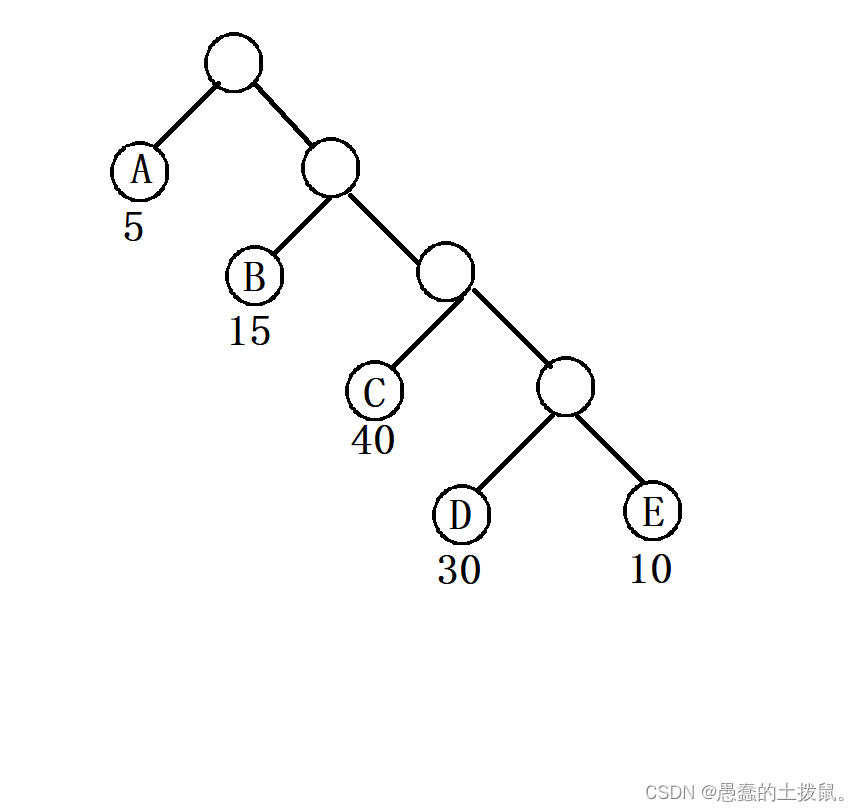
在这里插入图片描述
在上图中，根节点到节点D的路径长度是4，二叉树的路径长度=1+1+2+2+3+3+4+4=20。WPL(a)=51+152+403+304+10*4=315。

1.1 什么是哈夫曼树

假设有n各权值{w1,w2,…,wn}，构造一棵有n各叶子节点的二叉树，每个叶子节点带权wk，每个叶子的路径长度为lk，WPL=w1l1+w2l2+…+wn*ln，记带权路径长度WPL最小的二叉树为哈夫曼树，也称其为最优二叉树。

2.如何构造哈夫曼树（哈夫曼算法）

根据给定的n个权值{w1,w2,…,wn}构成n个二叉树的集合F={T1,T2,…,Tn}，其中每棵二叉树Ti中只有一个带权为wi的根节点，其左右子树均为空。
在F中选取两棵根节点的权值最小的树作为左右子树构造一个新的二叉树，且置新的二叉树的根节点的权值为其左右子树上根节点的权值之和。
在F中删除这两棵树，同时将新得到的二叉树加入F中。
重复步骤2和步骤3，直到F只含一棵树为止。这棵树便是哈夫曼树。

2.1 举例实现哈夫曼树

2.1.1手动实现具体步骤

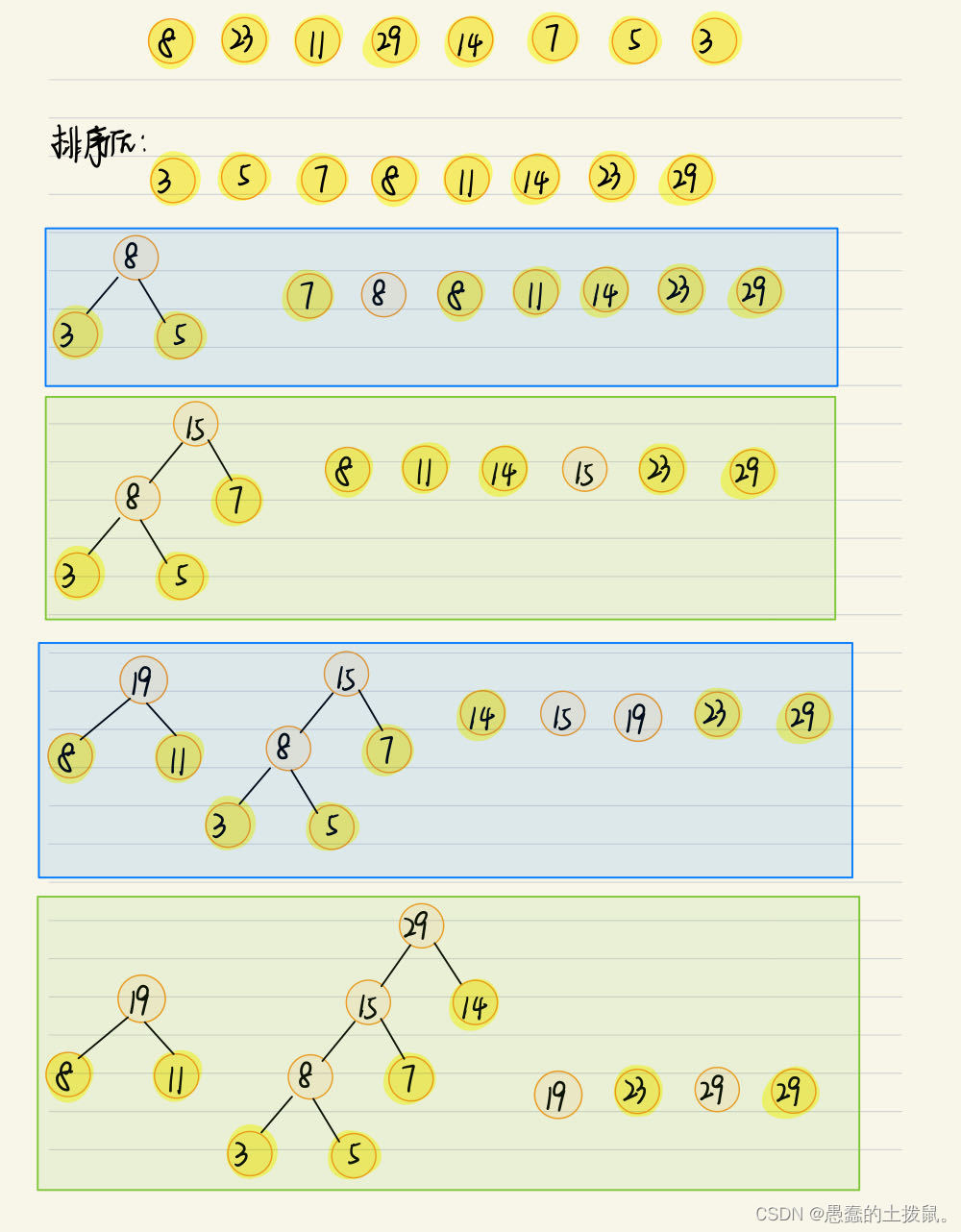
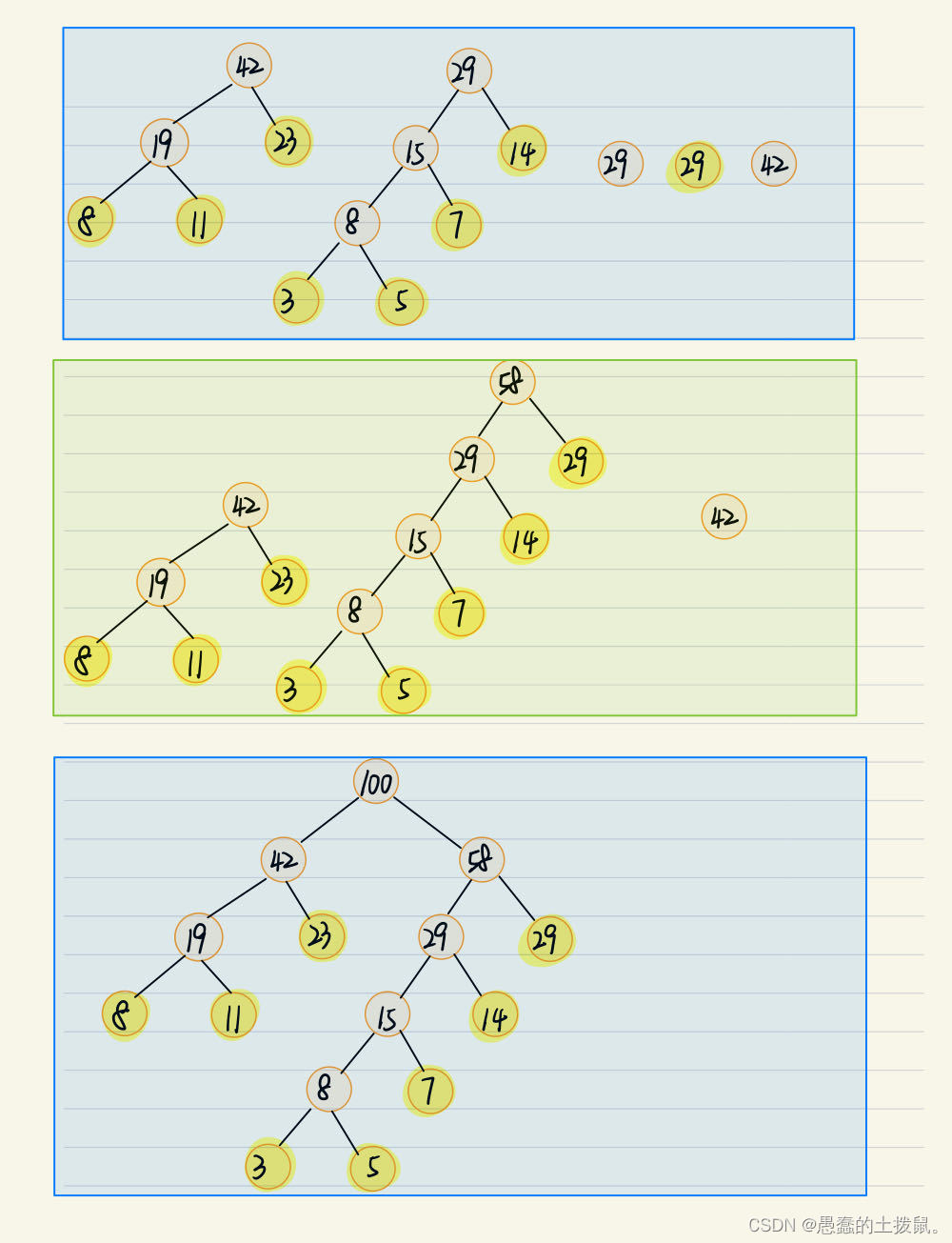
在这里插入图片描述

2.1.2代码实现具体步骤

注意：二叉树的存储以数组形式保存，而且0下标不存储元素，i下标的左孩子2*i，右孩子2*i+2.（之前有关二叉树的文章介绍过，大家可以自行查看）。

#include <iostream>
#include <vector>
#include <string>
#include <queue>

using namespace std;

typedef unsigned int WeigthType;

typedef unsigned int NodeType;

typedef struct
{
   
   
    WeigthType weight;
    NodeType parent, leftchild, rightchild;
}HNode;

typedef struct IndexWeight
{
   
   
    int index;
    WeigthType weight;
    operator WeigthType() const {
   
    return weight; }//按照权值比较
};



class HuffManTree
{
   
   
private:
    vector<WeigthType> w;
    vector<HNode> hft;
    int n = 0;
public:
    //构造函数（初始化Huffman树）  (叶子节点树，权重，hufman树)
    HuffManTree(vector<WeigthType> w1)
    {
   
   
        w = w1;
        n = w1.size();
        hft.resize(n * 2);
        
        for (int i = 1; i <= n; i++)
        {
   
   
            hft.at(i).weight = w[i-1];
        }        
    }

    void CreatHuffman()
    {
   
   
        //优先级队列
        priority_queue<IndexWeight, vector<IndexWeight>, std::greater<IndexWeight>> qu;
        for (int i = 1; i <= n; i++)
        {
   
   
            qu.push(IndexWeight{
   
    i,hft.at(i).weight });
        }

        int k = n +1;

        while (!qu.empty())
        {
   
   
            //左节点
            if (qu.empty()) break;
            IndexWeight left = qu.top();      qu.pop();
            //右节点
            if (