Codeforces Round #296 (Div. 1) D. Fuzzy Search-优快云博客

该博客讲述了在DNA序列中查找特定子串的问题，考虑到错误阈值k，定义了一种模糊匹配的方式。通过实例解释了匹配条件，并提供了一个计算在给定错误阈值下子串出现次数的算法思路。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

Leonid works for a small and promising start-up that works on decoding the human genome. His duties include solving complex problems of finding certain patterns in long strings consisting of letters 'A', 'T', 'G' and 'C'.

Let's consider the following scenario. There is a fragment of a human DNA chain, recorded as a string S. To analyze the fragment, you need to find all occurrences of string T in a string S. However, the matter is complicated by the fact that the original chain fragment could contain minor mutations, which, however, complicate the task of finding a fragment. Leonid proposed the following approach to solve this problem.

Let's write down integer k ≥ 0 — the error threshold. We will say that string T occurs in string S on position i (1 ≤ i ≤ |S| - |T| + 1), if after putting string T along with this position, each character of string T corresponds to the some character of the same value in string S at the distance of at most k. More formally, for any j (1 ≤ j ≤ |T|) there must exist such p (1 ≤ p ≤ |S|), that |(i + j - 1) - p| ≤ k and S[p] = T[j].

For example, corresponding to the given definition, string "ACAT" occurs in string "AGCAATTCAT" in positions 2, 3 and 6.

$\text{[math]}$

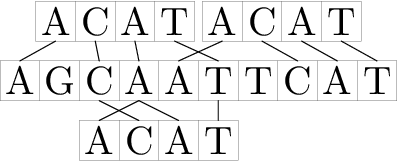
Note that at k = 0 the given definition transforms to a simple definition of the occurrence of a string in a string.

Help Leonid by calculating in how many positions the given string T occurs in the given string S with the given error threshold.

Input

The first line contains three integers |S|, |T|, k (1 ≤ |T| ≤ |S| ≤ 200 000, 0 ≤ k ≤ 200 000) — the lengths of strings S and T and the error threshold.

The second line contains string S.

The third line contains string T.

Both strings consist only of uppercase letters 'A', 'T', 'G' and 'C'.

Output

Print a single number — the number of occurrences of T in S with the error threshold k by the given definition.

Sample test(s)

input
10 4 1
AGCAATTCAT
ACAT

output
3

Note

If you happen to know about the structure of the human genome a little more than the author of the problem, and you are not impressed with Leonid's original approach, do not take everything described above seriously.

老实说这条题目一点意思都没有，将ACTG四个字母分开处理是很显然的，使用left+1，right-1的方法可以O（n）时间复杂度内将每个位置各字母是否valid求出来，之后我刚开始想直接用两层for循环比一下（毕竟这条时间是3s），不过TLE了，之后想到用bitset来算，之后就过了

代码：

#include <iostream>
#include <bitset>

#define DEBUG_OUT(a) 
#define DEBUG_OUT_INLINE(a) 

using namespace std;

const int max_n=200010;
int ns,nt,k;
int str_count[4][max_n];

char s[max_n];
char t[max_n];

bitset<max_n>s_bit[4];
bitset<max_n>ans;

int from_c_to_i(char c)
{
	switch(c){
		case 'A':
			return 0;
		case 'C':
			return 1;
		case 'G':
			return 2;
		case 'T':
			return 3;
		default:
			DEBUG_OUT("error :not ACTG");
			return -1;
	}
}

int cal_count()
{
	for(int i=0;i<ns;++i)
	{
		int index=from_c_to_i(s[i]);
		int left=(i-k>0)?i-k:0;
		int right=(i+k<ns)?i+k:ns-1;

		str_count[index][left]+=1;
		str_count[index][right+1]+=-1;
	}

	for(int i=0;i<4;++i)
	{
		for(int j=1;j<ns;++j)
		{
			str_count[i][j]+=str_count[i][j-1];
		}
	}

	for(int i=0;i<4;++i)
	{
		for(int j=0;j<ns;++j)
		{
			if(str_count[i][j]>0)
			{
				s_bit[i][j]=1;
			}
		}
	}

	for(int i=0;i<4;++i)
	{
		DEBUG_OUT("list:"<<i);
		for(int j=0;j<ns;++j)
		{
			DEBUG_OUT_INLINE(str_count[i][j]<<" ");
		}
		DEBUG_OUT("");
	}
}

int findall()
{
	int c=0;
	for(int i=0;i<ns-nt+1;++i)
	{
		ans[i]=1;
	}

	for(int i=0;i<nt;++i)
	{
		ans&=(s_bit[from_c_to_i(t[i])]>>i);
	}

	return ans.count();
}

int main()
{
	cin>>ns>>nt>>k;

	cin>>s;
	cin>>t;

	DEBUG_OUT("all in");

	cal_count();

	DEBUG_OUT("count end");

	cout<<findall()<<endl;
}