堆的基本性质与排序算法的实现_一堆性质-优快云博客

这篇博客回顾了堆的基本性质，特别是最大堆和最小堆的概念，以及它们在数据结构中的应用。作者通过错误的面试经历强调了理解堆中父子节点关系的重要性，并解释了堆排序的时间复杂度。堆排序的维护、建堆过程和相关代码实现也被详细讨论，旨在帮助读者更好地掌握堆排序算法。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

前段时间申了腾讯移动开发暑期实习，昨天一轮面试被问到堆的问题（面试官人很好~）。这里的堆是数据结构中的堆，而不是操作系统的堆。然而，堆排序时间太久了，忘掉了一些基本概念，于是面试不出意外是挂掉了（当然不止堆没答上来）。这里总结一下堆的性质，为以后申公司做好准备吧！

腾讯面试官问了我一个问题，说100个数字存放在堆中，最差时间找到这个数字是多少。我不确定，先是回答了一个O(nlgn)，后来他要具体的数字，我突然断电了，想成了二叉搜索树，于是回答了“7”。。。。。于是就很尴尬了T_T

我们先看看什么是数据结构中的堆：

（二叉）堆是一个二叉树，可以由数组构成，也可以由链表构成。它可以被看成一棵近似的完全二叉树，树上的每一个节点对应数组或链表中的每一个元素。

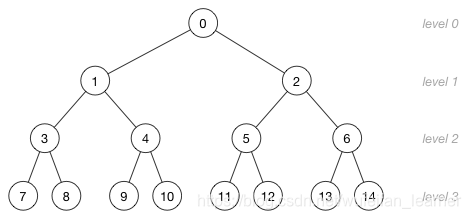
（借图说话，侵删）

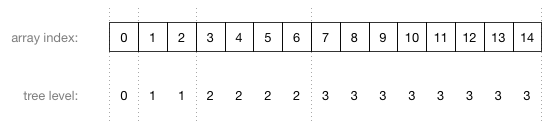
由于堆可以近似成一棵完全二叉树，所以完全二叉树有的性质（父节点与孩子节点的位置关系）堆是共享的。

//给定节点i，以下为其家族节点位置
Parent(i){
    return i/2;
}

Left(i){
    return 2i;
}

Right(i){
    return 2i+1;
}

一般来说，二叉堆分为最大堆和最小堆，又称大顶堆和小顶堆，我认为后者更形象。意思就是堆顶（树根）的数是最