JPEG编码器的硬件实现

1、JPEG编码器的基本结构

JPEG编码器（本文只讨论baseline JPEG）的硬件设计主要由7个模块组成：

1）YUV Process主要实现YUV亚采样、8x8 block重排列等功能，是JPEG编码的预处理模块；

2）2D-DCT即二维离散余弦变换，完成空间域到频域的转换；

3）QT&ZigZag是量化和数据重排列，量化精度决定了压缩率，也是图像质量损耗的主要因素；

4）RLE是游程编码，以无损的方式压缩量化产生的大量0；

5）Huffman编码也是无损的，它的主要目的是将高频出现的数据用短码表示，而将低频出现的数据用长码表示，从而在整体上实现数据压缩的效果；

6）JFIF Header是给压缩后的JPEG数据加上包头，从而输出完整的JPEG码流；

7）Register Bank是寄存器控制单元，一般通过控制总线（如AXI lite、APB）连接到系统主控（如CPU）。

2、YUV Process

原始图像需要转换到YUV域并进行sub sample，这里以YUV420举例。JPEG处理一幅图像是按照MCU（Minimum Coded Unit）为滑窗单元，MCU的大小并不固定，跟YUV sub-sample以及算法选择都有关系。

这里以16x16 MCU举例，在进入JPEG encoding之前，还需要把MCU拆分成6个8x8的block，它们的顺序是Y/Y/Y/Y/U/V。

3、2D-DCT

二维离散余弦变换的硬件实现有很多快速算法，这里只是介绍一种比较通用好理解的实现方法，PPA并非最优。

二维离散余弦变换的公式如下图示。为了减少运算次数、节省硬件资源，可以将二维的离散余弦变换拆分成两次一维的离散余弦变换。可以看到，拆分后的两次一维变换具有完全相同的形式和参数。在具体实现中，还可以利用变换的对称性，提取相同系数，从而减少乘法的次数。

2D-DCT以8x8 block作为基本处理单元，第一次DCT先对行进行处理，输出也是8x8的矩阵；第二次DCT再对列进行处理，输出最终结果的8x8矩阵。

4、QT&Zig-Zag

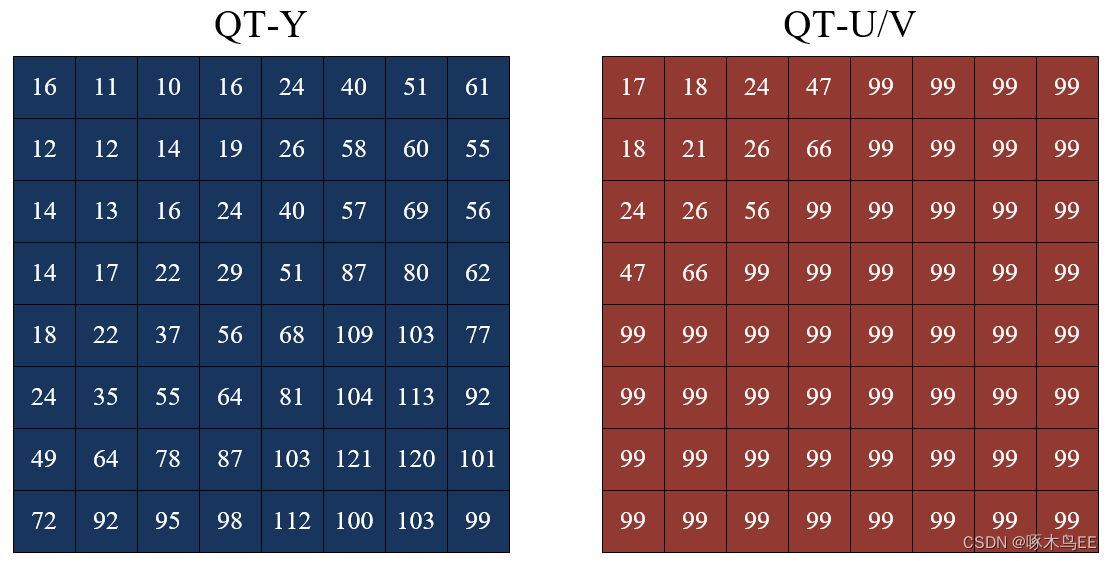
所谓量化，就是拿2D-DCT的结果去除以一个系数。一个8x8 block内的每一个元素要除的系数都不相同，所以这些系数也组成了一张8x8的矩阵（量化表，即QT）。此外，Y和UV的量化策略是不同的，所以一共有两张QT表。下图是标准QT表。

对QT表进行调整即可改变压缩率，那么QT表如何调整呢？答案是下面的公式：

Q0(u,v)即标准QT表中的值，QF(Quality Factor)是质量因子，代表图像质量的好坏，QF越大，Q(u,v)越小，数据被量化后保留的细节也就越多，图像质量越高。当QF=100时，Q(u,v) = 1，理论上就是无损量化。

在硬件实现中，乘法比除法消耗更少的资源，所以实际使用的是QT的倒数表（取倒数后左移取整），量化计算就变成乘法了。

2D-DCT得到的是8x8 block的频率信息，从左上到右下，频率逐渐升高，其中左上第一个数值是该block的DC分量。量化后高频区域会产生大量的0，如果还按照Z字形扫描，就不利于把这些0集中在一起，后面RLE模块就不能发挥最大价值。所以我们按照频率递增的方向将量化后的数据进行Zig-Zag重排，从而将尽可能多的0集中在一起。

5、RLE

RLE(Run Length Encoding)即游程编码，其原理很简单，就是把连续的0用NUM标记，从而压缩数据体积。

下面解释一下RLE的具体规则：

1）block的第一个数据为DC，其余63个数据是AC；

2）DC采用的是差值编码，即ΔDn = Dn – Dn-1，注意，Y/U/V有他们各自的ΔDn，不能混在一起；

3）AC采用游程编码，分为两部分（NUM, VALUE），NUM表示当前非零值到前一个非零值之间共有几个0，VALUE即当前的非零值；

4）如果两个非零值之间有超过16个0，则用ZRL（15,0）来标记连续16个0，但是要注意，EOB之前的ZRL是无效的，必须删除；

5）如果block的最后一个数据是0，那么从这个0开始一直到前一个非零值之间的所有0，都可以用EOB（0,0）来标记，这也是为什么EOB之前的ZRL是无效的原因。

举个例子：

RLE input：

RLE output：

block-1: (0,88), (0,57), (0,45), (4,23), (1,-30), (0,-16), (2,1), (15,0), (3,5), (0,0)

block-2: (0,-22), (0,95), (5,77), (3,-8), (15,0), (0,2), (0,0)

6、Huffman Encoder

Huffman code的思想是，将数据拆分成一个个符号（Symbol），统计每个符号出现的频率，根据频率构建出二叉树。之后根据二叉树，为每个符号值分配二进制位编码，频率越高，编码越短，频率越低，编码越长，从而实现整体上的数据压缩。

根据其原理不难理解，要想正确解码，除了要保存编码后的二进制位，还需要保存二叉树信息，这样解码器才能知道符号值和编码值的对应关系。假如保存二叉树本身就占太多空间，那么对于少量数据而言，压缩后总数据量反而会更大，这就得不偿失了。所以要利用好Huffman code，最关键的就是如何用尽量少的空间保存二叉树信息。

Baseline JPEG采用的是Canonical Huffman Code（范式霍夫曼编码），所谓范式，即对Huffman code施加某些强制规定，从而能够利用很少的数据便能重构出符号和编码的对应关系。因为规则固定，所以硬件上很容易使用查找表（LUT）的方式来实现Huffman Encoding。下面解释一下JPEG使用的Huffman表，其中，Y和UV各自有两张表，一张是DC表，一张是AC表，这样总共会用到4张表。

表一：DC-0

HT index	00 01 05 01 01 01 01 01 01 00 00 00 00 00 00 00
HT encode	00 01 02 03 04 05 06 07 08 09 0A 0B

HT index是一个索引表，包含16 Byte，从左到右依次表示位数为1~16bit的Huffman编码各有几个。比如第一字节是00，表示没有位数为1bit的编码。第二字节是01，表示位数为2bit的编码有一个。第三字节是05，表示位数为3bit的编码有5个，以此类推。Huffman编码本身是二进制递进的，但在跨越index字节的时候需要左移1bit（这是为了保证每个Huffman编码的独特性，否则在解码的时候就找不到边界了），由此我们可以得到下面的Huffman树：

编码bit