栈和队列的基本概念笔记

最新推荐文章于 2022-10-24 20:02:31 发布

原创最新推荐文章于 2022-10-24 20:02:31 发布 · 260 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#数据结构 #队列

本文深入探讨了数据结构中的栈、队列与数组，详细讲解了它们的基本概念、存储结构和常见应用。通过实例解析，帮助读者理解栈的后进先出特性、队列的先进先出特性，以及数组的多维存储方式。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

第三章栈和队列

一、栈

1、基本概念

栈（stack）：只允许在一端进行插入删除操作的线性表。后进先出（LIFO），
输出序列
- 连续输入输出情况下：输出序列与输入序列相反
- 非连续输入和输出：出栈序列中每一个元素后面所有比他小的元素组成一个递减序列
- 合法出栈序列个数：
  f(n) = f(0) * f(n-1) + f(1) * f(n-2) + … + f(n-2) * f(1) + f(n-1) * f(0)
  即f(n) = C(2n,n) / (n+1)
  且f(0) = f(1) = 1

栈的基本操作：

//头文件 
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<malloc.h>
 
//宏定义 
#define  TRUE  1
#define  FALSE 0
#define  OK    1
#define  ERROR 0
#define  INFEASIBLE -1
#define  OVERFLOW   -2
#define  STACK_INIT_SIZE  100
#define  STACKINCREMENT    10
typedef  int  ElemType;
typedef  int    Status;
 
//栈的顺序结构表示 
typedef struct
{
    ElemType *base;
    ElemType *top;
    int stacksize;
}SqStack;
 
//1.构建一个空栈 
Status InitStack(SqStack &S)
{
    S.base = (ElemType*)malloc(STACK_INIT_SIZE*sizeof(ElemType));
    if (!S.base)
        exit(OVERFLOW);//存储分配失败
    S.top = S.base;
    S.stacksize = STACK_INIT_SIZE;
    return OK;
}
 
//2.销毁栈 
Status DestroyStack(SqStack &S)
{
    S.top = NULL; 
    S.stacksize = 0; 
    free(S.base); 
    return OK;
}
 
//3.清空栈 
Status ClearStack(SqStack &S)
{
    S.top = S.base;
    return OK;
}
 
//4.判断栈是否为空 
Status StackEmpty(SqStack S)
{
    if (S.top == S.base)
        return ERROR;
    else
        return TRUE;
}
 
//5.求栈的长度 
Status StackLength(SqStack S)
{
    if (S.top == S.base)
        return FALSE;
    else
        return (S.top - S.base);//也可以直接返回S.top - S.base
}
 
//6.//求栈顶元素 
Status GetTop(SqStack S, ElemType &e)
{
    if (S.top == S.base)
        return FALSE;
    else
        e = *(S.top - 1);
    return e;
}
 
//7.栈顶插入元素 
Status Push(SqStack &S, ElemType &e)
{
    if (S.top - S.base >= STACK_INIT_SIZE)
    {
        S.base = (ElemType *)realloc(S.base, (S.stacksize + STACKINCREMENT) * sizeof(ElemType));
        if (!S.base)
        {
            return false;
        }
        S.top = S.base + STACK_INIT_SIZE;//栈底地址可能改变，重新定位栈顶元素
        S.stacksize = S.stacksize + STACKINCREMENT;
    }
    *S.top = e;
    S.top++;
    return OK;
}
 
//8.删除栈顶元素 
Status Pop(SqStack &S, ElemType &e)
{
    if (S.top == S.base)
        return ERROR;
    else
    {
        S.top--;
        e = *S.top;//说明：此处容易使人迷惑，实际上此元素并没真正删除，仍在S.top中，但是如果插入元素，就会被更新，就像是删除了一样
        return e;
    }
}
 
//9.遍历栈 
Status StackTraverse(SqStack S)
{
    if (S.base == NULL)
        return ERROR;
    if (S.top == S.base)
        printf("栈中没有元素……\n");
    ElemType *p;
    p = S.top;
    while (p > S.base)
    {
        p--;
        printf("%d ",*p);
    }
 
    return OK;
}
 
//主函数检验九种操作 
int main()
{
    SqStack S;
    printf("构造一个空栈……\n");
    InitStack(S);
    int i,n ;
    printf("输入栈的长度:\n");
    scanf("%d",&n);
    for (i = 1; i <= n; i++)
    {
        printf("输入栈的第%d个元素\n",i);
        ++S.top;
        scanf("%d",S.top-1);
    }
     printf("……本栈是空栈吗？？……\n");
    if (StackEmpty(S) == 1)
         printf("NO !!!\n");
    else
         printf("YES !!!\n");
     printf("……求出栈的长度……\n");
    int m;
    m = StackLength(S);
     printf("栈的长度是:\n");
     printf("%d\n",m);
     printf("遍历输出栈中的所有元素:\n");
    StackTraverse(S);
     printf("\n");
     printf("……输出栈顶元素……\n");
    int e;
    e = GetTop(S, e);
     printf("栈顶元素是:\n");
     printf("%d\n",e);
     printf("……栈顶插入元素……\n");
     printf("请输入要插入的元素的数值:\n");
    scanf("%d",&e);
    Push(S,e);
     printf("现在栈中的元素是:\n");
    StackTraverse(S);
     printf("\n");
     printf("……栈顶删除元素……\n");
    e = Pop(S,e);
     printf("被删除的元素是:\n");
    scanf("%d",&e);
     printf("现在栈中的元素是:\n");
    StackTraverse(S);
     printf("\n");
     printf("……清空栈……\n");
    ClearStack(S);
     printf("现在栈中的元素是:\n");
    StackTraverse(S);
     printf("……销毁栈……\n");
    if(DestroyStack(S)==1)
         printf("销毁栈成功\n");
    else
         printf("销毁栈失败\n");
     printf("喜您成功完成所有的功能!\n");
    return 0;
}

2、存储结构

顺序存储

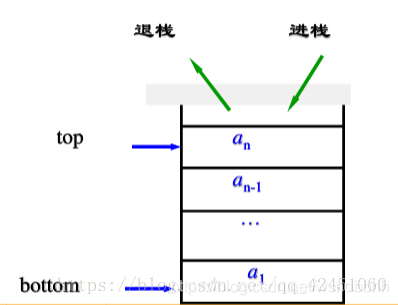
栈空条件：S.top==-1
栈长：S.top+1
栈满条件：S.top==MaxSize-1

栈的基本操作：

初始化：

void InitStack(SqStack &S){
	S.top==-1;
}

判断栈空

bool StackEmpty(SqStack S){
	if(S.top==-1)
		return true;
	else
		return false;
}

进栈

bool Push(SqStack &S,ElemType x){
	if(S.top==MaxSize-1)//栈满
		return false;
	S.data[++S.top]=x;//先+1，后赋值
	return true;//入栈成功
}

出栈

bool Pop(SqStack &S,ElemType &x){
	if(S.top==-1)
		return false;
	x=S.data[S.top--];
	return true;//出栈成功
}

读出栈顶元素

bool GetTop(SqStack &S,ElemType &x){
	if(S.top==-1)
		return false;
	x=S.data[S.top];
	return true;
}

共享栈：将两个栈底设置在共享空间的两端，栈顶向空间中间延伸
- 判空：0号栈top==-1；1号栈top==MaxSize;
- 栈满：top1-top0==1
- 优点：存取时间复杂度为O（1），但空间利用更加有效

链式存储
链栈：采用链式存储的栈，所有操作都在表头进行

将链表的头部作为栈顶，尾部作为栈底
```
typedef struct Linknode{
	ElemType data;
	struct Linknode *next;
}*LiStack;
```

3、栈的应用

括号匹配
- 匹配序列：( [ ] ) [ ]、( [ ( ) ] )、( ) [ ( ) ]
- 不匹配序列：( [ ( ) ] 、] [ ] ( )、( ] [ ( ) ]
- 算法思想：
  1、初始一个空栈，顺序读入括号
  2、若是右括号，则与栈顶元素进行匹配。若匹配，则弹出栈顶元素；若不匹配，则该序列不合法
  3、若是左括号，则压入栈中
  4、若是全部元素遍历完毕，栈中非空则序列不合法
表达式求值
- 前缀表达式：+AB
  [ ( A + B ) * C ] - [ E - F ] = - * + A B C - E F
- 中缀表达式：A+B
- 后缀表达式：AB+
  [ ( A + B ) * C ] - [ E - F ] = A B + C * E F - -
- 算法思想：
  数字直接加入后缀表达式运算符时：
  a.若为“（”，入栈
  b.若为“）”，则依次把占中的运算符加入后缀表达式，直到出现“（”，并从栈中删除“）”
  c.若为’+’ ‘-’ ‘*’ ‘/’
  栈空：入栈
  栈顶元素为“（”，入栈
  高于栈顶元素优先级，入栈
  否则，则依次弹出栈顶元素运算符，直到一个优先级比他低的运算符或 ‘（’ 为止
  d.遍历完成，若栈非空依次弹出所有元素
递归
- 若在一个函数、过程或数据结构的定义中又应用了自身，则称它为递归定义的，简称递归。
- 递归的精髓在于能否将原问题转换为属性相同但规模较小的问题
- 菲波那切数列：0,1,1,2,3,5，，，
```
int Fib(int n){
	if(n==0)
		return 0;//递归出口
	else if(n==1)
		return 1;//递归出口
	else
		return Fib(n-1)+Fib(n-2);//递归表达式
}
```
- 递归产生的问题
  - 在递归调用过程中，系统为每一层的返回点、局部变量、传入实参等开辟了递归工作栈来进行数据存储，递归次数过多容易造成栈溢出
  - 通常情况下递归的效率并不高
  - 递归转换算法转换为非递归算法，往往需要借助栈来进行

二、队列

1、基本概念

队列：只允许在表的一端进行插入，表的另一端进行删除操作的线性表。先进先出（FIFO）。在队尾添加元素，在队头删除元素。
输出序列
- 连续输入输出情况下：输入序列与输出序列相同
- 非连续输入和输出：出栈序列中每一个元素后面所有比他小的元素组成一个递减序列
队列的基本操作
- InitQueue(&Q)：初始化队列，构造一个空队列Q
- QueueEmpty(Q)：判队列空，若队列Q为空，返回true，否则返回false
- EnQueue(&Q,x)：入队，若队列Q未满，则将x加入使之成为新的队尾
- DeQueue(&Q,&x)：出队，若队列Q非空，则删除队头元素，并用x返回
- GetHead(Q,&x)：读队头元素，若队列Q非空则用x返回队头元素
- ClearQueue(&Q)：销毁队列，并释放队列Q占用的内存空间

2、存储结构

顺序存储

队列结构体

#define MaxSize 50
typedef struct{
	ElemType data[MaxSize];
	//初始时front==rear==0
	int front,rear;//出队，入队指针，front指向队头元素，rear指向队尾元素的下一位置
}SqQueue;

队空条件：Q.front==Q.rear
队长：Q.rear-Q.front

循环队列：把存储队列的顺序队列在逻辑上视为一个环

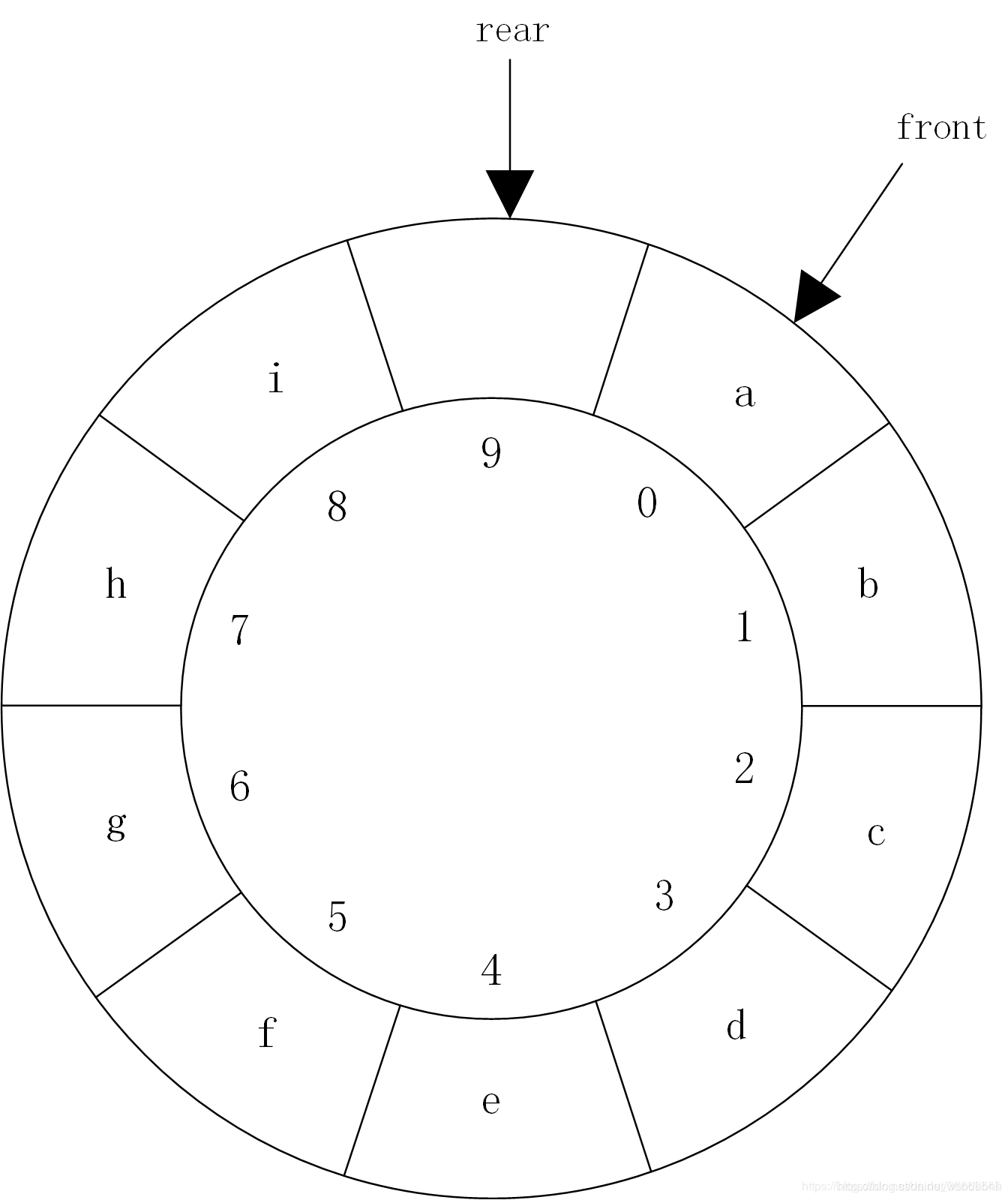
% MaxSize：取余
front指针移动：Q.front = (Q.front +1) % MaxSize
rear指针移动：Q.rear = (Q.rear + 1) % MaxSize
队列长度：（Q.rear + MaxSize - Q.front）% MaxSize
如何区分队空队满？
- 1、牺牲一个存储单元
  队空条件：Q.font == Q.rear
  队满条件：Q.font == (Q.rear + 1) % MaxSize
- 2、增加一个变量代表元素的个数
  队空条件：Q.size == 0
  队满条件：Q.size == MaxSize
- 3、增加tag标识
  队空条件：Q.front == Q.rear&&tag == 0
  队满条件：Q.front == Q.rear&&tag == 1

循环队列初始化：

void InitQueue(SqQueue &Q){
	Q.rear = Q.front = 0;
}

判断队空：

bool isEmpty(SqQueue Q ){
	if(Q.rear==Q.front)
		return true;
	else
		return false;
}

入队

bool EnQueue(SqQueue &Q,ElemType x){
	if(Q.front==(Q.rear + 1) % MaxSize)//满队列
		return false;
	Q.data[Q.rear] = x;//元素入队
	Q.rear = (Q.rear + 1) % MaxSize;//尾指针向后移一位
	return true;
}

出队

bool EnQueue(SqQueue &Q,ElemType x){
			if(Q.front == Q.rear )//空队列
				return false;
			x = Q.data[Q.front];//将x赋给当前的front指针指向的数据元素
			Q.front = (Q.front + 1) % MaxSize;//front指针向前移一位
			return true;
		}

链式存储

链队：采用链式存储的队列

节点结构体

typedef struct{
	ElemType data;//数据域
	struct LinkNode *next;//下一个节点的指针
}LinkNode;

链队结构体

typedef struct{
	LinkNode *front,*rear;
}LinkQueue;

初始化

void InitQueue(LinkQueue &Q){
	Q.front = (LinkNode *)malloc(sizeof(LinkNode));//初始化头节点
	Q.rear = Q.front;
	Q.fornt->next = NULL;	
}

判空

void isEmpty(LinkQueue Q){
	if(Q.front == Q.rear)
		return true;
	else
		return false;
}

入队

void EnQueue(LinkQueue &Q,ElemType x){
	LinkNode *s = (LinkNode *)mallod(sizeof(LinkNode));//为s申请一个节点空间
	s->data = x;
	s->next = null;
	Q.rear->next = s;
	Q.rear = s;
}

出队

bool DeQueue(LinkQueue &Q,ElemType &x){
	if(Q.front == Q.rear)
		return false;
	LinkNode *p = Q.front->next;//创建指针类型p，保存该节点地址
	x = p->data;//数据元素保存到x中
	Q.front->next = p->next;//删除操作，头节点的next指针指向下一个节点的next指针
	if(Q.rear == p)//如果链队只有一个节点
		Q.rear = Q.front;//空队
	free(p);
	return true;
}

双端队列
允许两端都可以进行入队及出队的操作
输入受限的双端队列：有一端只能输入
输出受限的双端队列：有一端只能输出

3.队列的应用

层次遍历
计算机系统

三、数组

1、数组的定义

数组是由n（n>=1）个相同类型的数据元素构成的有限序列，没个数据元素称为一个数组元素，每个元素受n个线性关系的约束，每个元素在n个线性关系中的序号称为该元素的下标，并称该数组为n维数组

数组的维度
- 一维数组：（a0，a1，a2，a3，a4）
- 二维数组：[ （a0,0，a0,1，a0,2），（a1,0，a1,1，a1,2）]
数组的维度和维界不可变
数组一旦被定义，其维度和维界不可变，数组除初始化和销毁外，只有存取元素和修改元素的操作

2、数组的存储结构

顺序存储：

按行优先：LOC（ai,j）= LOC（a0,0）+ i * （n+1）L + j * L
按列优先：LOC（ai,j）= LOC（a0,0）+ j * （n+1）L + i * L

3、矩阵的压缩存储

概念
- 压缩存储：指多个值相同的元素只分配一个存储空间，对零元素不分配存储空间
- 特殊矩阵：指具有许多相同矩阵元素或零元素，并且这些相同矩阵元素或零元素的分布有一定规律性的矩阵
- 特殊矩阵的压缩存储：找出特殊矩阵中值相同的矩阵元素的分布规律，把那些呈现规律性分布、值相同的多个矩阵元素压缩存储到一个存储空间上
不同矩阵的压缩存储
- 对称矩阵（按行存储）
  数组下标k = i（i - 1）/ 2 + （j - 1）（i >= j）即下三角
  数组下标k = j（j - 1）/ 2 + （i - 1 ）（i < j）即上三角
- 三角矩阵（按行存储）
  存放数组B[n（n+1）/ 2 + 1]（+1表示把常量C存放到数组中）
  - 下三角矩阵：
    数组下标k = i（i - 1）/ 2 + （j - 1）（i >= j）
    数组下标k = n（n+1）/ 2（i < j）
  - 上三角矩阵
    数组下标k = （i - 1）（2n - i + 2）/ 2 + （j - 1）（i <= j）
    数组下标k = n（n+1）/ 2（i > j）
- 三对角矩阵（按行存储）
  数组下标：k = 2i + j - 3
  若k已知，求i，j？
  i = （k+1）/ 3 +1
  j = k - 2i +3
- 稀疏矩阵
  三元组（行标、列标、值）
  稀疏矩阵压缩存储后失去了随机存储的特性