Steady-State Methods for Simulating Analog and Microwave Circuits, Chapter 1 Introduction

Chapter 1 Introduction

1. 基本思想
   利用改进节点分析，根据基尔霍夫电流定律和元件的本构方程，构建描述电路行为的方程，数值积分算法将其近似为隐式代数方程，再用牛顿-拉夫逊迭代法求得节点电压解。

2. 稳态解
   是微分方程中随着初始条件影响逐渐消失而渐近趋近的解，可能有零个、一个或多个稳态解，且稳态解可能具有渐近稳定性。包括：
   DC稳态（解为电路的平衡点，不随时间变化）
   sss正弦稳态（渐近稳定的线性电路在正弦源驱动下最终呈现的纯正弦或含直流偏移的正弦稳态）
   pss周期稳态（直流偏移和无限个谐波相关的正弦波线性组合而成，可能源于自振荡或周期性输入）
   qpss准周期稳态（非线性电路在多个不相关频率的周期源驱动下的稳态响应，周期稳态的特殊情况）
   

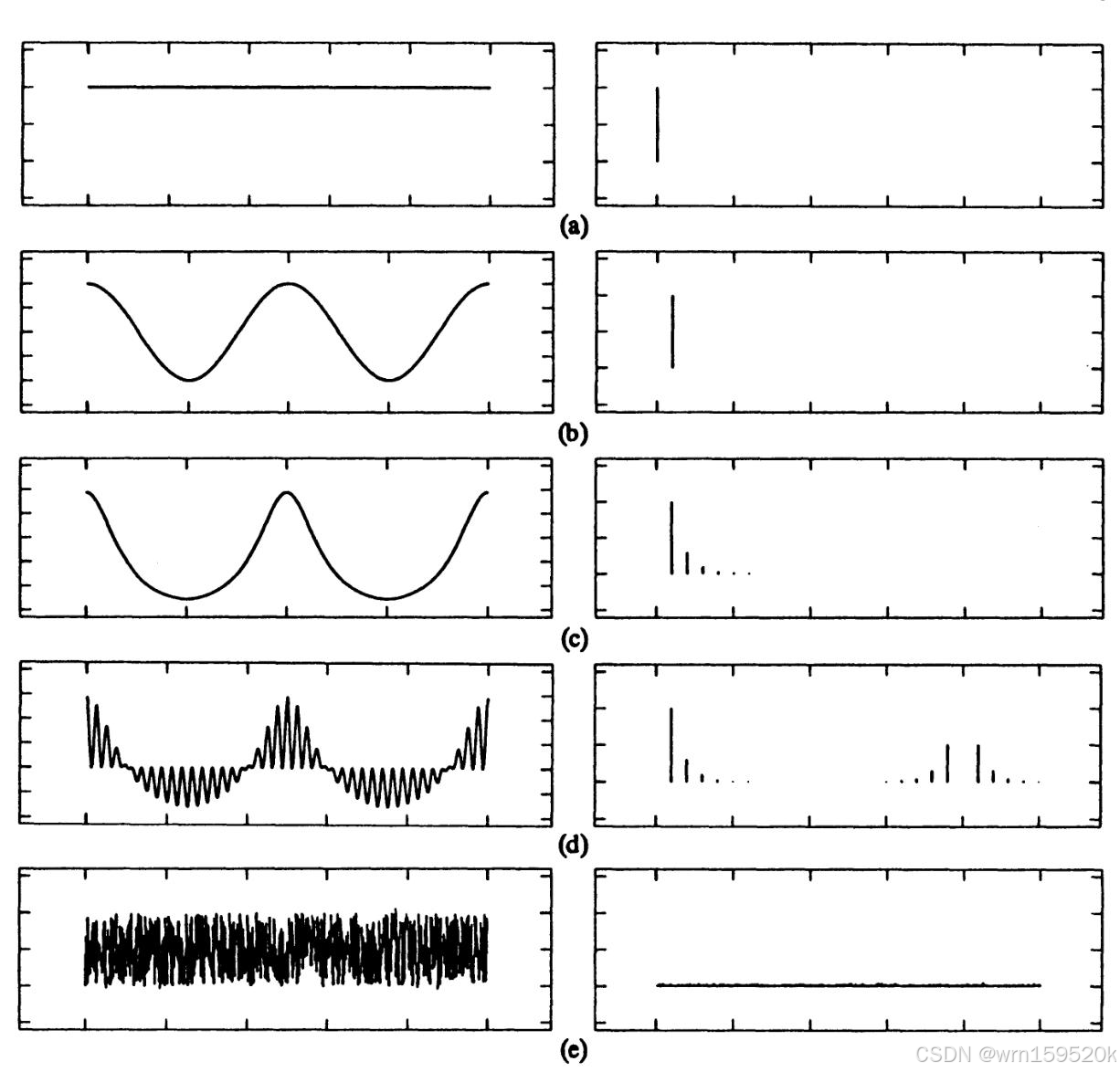
Page 6, Steady-State Methods for Simulating Analog and Microwave Circuits, Kenneth S. Kundert,1990

3. 分布式器件
   传输线等分布式器件的电压和电流沿其长度变化显著，影响电路性能，其行为需通过求解波动方程来计算，利用卷积积分计算终端电流。在频域中，由于分布式器件的线性特性，计算相对容易，可通过求解频域方程得到频域解。

4. 计算稳态解
   高频信号的变化需要的时间步长非常精细，低频信号会使电路缓慢达到稳态从而增大了数值积分的时间区间，通过三角多项式积分方法或跟踪包络解来同步振荡周期和时间步长的数量级。

   时域方法：寻找周期稳态解，本质上要确定电路微分方程的初始条件，使得一个周期结束时的解与初始解相匹配，将电路稳态响应转化为边值问题，即：$$x^{\prime }(t)=f(x(t),t);g(x(0),x(T))=0;$$

   1) Shooting: 猜测初始解，进行一个周期仿真，检查是否匹配，不断猜测，转化成多个初值问题
   2) 有限差分法：利用离散差分代替连续导数，将微分方程转化成代数方程与边界条件联立

   频域方法：三角级数表示稳态解，当解类似正弦函数时，时域方法需要的时间步长非常精确来利用多项式近似结果。非线性积分 - 微分方程难以求解，三角级数将其转化成代数方程，通过线性子电路和非线性子电路的电流平衡构建。