XJTUSE 数据结构与算法第四次作业——任务2_南洋理工大学数据结构与算法作业-优快云博客

任务2

题目

为了确保每次迷宫的生成都是成功的，将不再采用任务 1 中的随机擦除边的生成方式，而是采用 Kruskal 最小支撑树的算法来实现迷宫生成。具体的执行步骤如下：

1. 为任务 1 中用来表示迷宫的图中的每一条边都随机生成一个权值（此时的图是一个带权图，所以在表示时可能会和任务 1 的表示有出入，请注意这个细节）；

2. 利用 Kruskal 算法对步骤 1 中的图生成最小支撑树 T；

3. 将 T 中的每一条边相对应在迷宫中的边擦除掉，此时迷宫就生成了，这样生成的迷宫一定是成功的。

数据设计

Kruskal算法算法步骤：

1.设连通网 N = (V, E )，令最小生成树初始状态为只有 n 个顶点而无边的非连通图 T=(V, { })，每个顶点自成一个连通分量。

2.在 E 中选取代价最小的边，若该边依附的顶点落在 T 中不同的连通分量上（即：不能形成环），则将此边加入到 T 中；否则，舍去此边，选取下一条代价最小的边。

3.依此类推，直至 T 中所有顶点都在同一连通分量上为止。

这个算法需要如下几种数据结构：

我们需要利用并查集树UnionFindTree判断结点是否连通，以及连通两个非连通分量。
并查集树和Kruskal算法需要树节点Node。
我们还需要利用最小优先队列MinPriorityQueue优化边的查找与删除。
我们需要为Graph多加些方法，需要Graph2继承Graph1。
还需要利用队列LQueue。
边Edge。

并查集树UnionFindTree：

构造函数UnionFindTree(Node[] set)接受一个Node数组作为参数，用于初始化并查集。

public class UnionFindTree {
//用树实现并查集
public Node[] set;
public UnionFindTree(Node[] set) {
this.set = set;
}
}

find(int i)方法用于查找元素i所属的集合名字（即根节点的下标）。在查找的过程中，使用了路径压缩的优化方式：将路径上的所有节点的父指针直接指向根节点，从而使得树的深度更加平衡。

/**
* 返回包含给定元素的集合名字
*
* @param i 元素下标
* @return 以根结点下标作为集合名字
*/
public int find(int i) {
//使用路劲压缩法：在查找某个元素是否属于某个集合时，将该结点到根结点路径上
// 所有结点的父指针全部改为指向根结点，这种方式可以产生极浅的树
Node current = set[i];
if (current.getParent()<0)
return i;
return current.setParent(find(current.getParent()));
}

union(int i, int j)方法用于将两个元素i和j所属的集合进行合并。首先找到两个元素所在集合的根节点，然后根据根节点所表示的树的大小（即节点数的负值）来决定合并的方式。将节点数少的一棵树的根节点的父节点设置为节点数多的一棵树的根节点，并更新节点数。

/**
* 生成一个新的集合，该集合是i所属的集合set1和j所属的集合set2的并集
*
* @param i
* @param j
*/
public void union(int i, int j) {
//使用重量平衡原则
int root1 = find(i);
int num1 = set[root1].getParent();
int root2 = find(j);
int num2 = set[root2].getParent();
if (num1 <= num2) {
set[root1].setParent(num1+num2);
set[root2].setParent(root1);
//将其中结点数少的一棵树的根结点的父结点设置为
//结点数多的一棵树的根结点
} else {
set[root2].setParent(num1+num2);
set[root1].setParent(root2);
//将其中结点数少的一棵树的根结点的父结点设置为
//结点数多的一棵树的根结点
}
}

isConnected(int i, int j)方法用于判断元素i和元素j是否在同一个集合中，即判断它们的根节点是否相同。

/**
* 判断元素i和元素j是否在同一个分组中
* @param i
* @param j
* @return
*/
public boolean isConnected(int i,int j){
return find(i)==find(j);
}
public void print() {
for (int i = 0; i < set.length; i++) {
System.out.print(set[i].getElement() + " ");
}
}

print()方法用于打印当前并查集中所有元素的值。这里不再给出。

测试一下：

public static void main(String[] args) {
// 创建一组元素，共有8个元素
Node[] set = new Node[8];
for (int i = 0; i < set.length; i++) {
set[i] = new Node(i, -1); // 初始时每个元素都是一个独立的集合，父节点为-1
}
UnionFindTree unionFind = new UnionFindTree(set);
// 合并一些集合
unionFind.union(0, 1);
unionFind.union(2, 3);
unionFind.union(4, 5);
unionFind.union(6, 7);
unionFind.union(0, 2);
unionFind.union(4, 6);
unionFind.union(0, 4);
// 验证元素之间的连通性
System.out.println("0 和 7 是否连通？" + unionFind.isConnected(0, 7));
System.out.println("1 和 3 是否连通？" + unionFind.isConnected(1, 3));
System.out.println("2 和 6 是否连通？" + unionFind.isConnected(2, 6));
System.out.println("4 和 5 是否连通？" + unionFind.isConnected(4, 5));
// 打印并查集中的元素
unionFind.print();
}

结果如下：

图5 并查集树测试结果

并查集树树节点Node：

package homework02;
public class Node {
private int parent;//父结点下标
private Object element;//存储元素内容
public Node() {
this(null, -1);
}
public Node(Object element) {
this(element, -1);
}
public Node(Object element, int parent) {
this.element = element;
this.parent = parent;
}
public int getParent() {
return parent;
}
public int setParent(int parent) {
return this.parent = parent;
}
public Object getElement() {
return element;
}
public void setElement(Object element) {
this.element = element;
}
}

最小优先队列MinPriorityQueue：

MinPriorityQueue有三个构造方法：

MinPriorityQueue(): 无参构造函数。创建一个默认大小（DEFAULT_CAPACITY）的最小优先队列，初始化了数组array，并将currentSize设置为0。

MinPriorityQueue(int size): 带参构造函数。创建一个指定大小的最小优先队列，初始化了数组array，并将currentSize设置为0。

MinPriorityQueue(T[] array): 带参构造函数。使用给定的数组创建一个最小优先队列。首先创建一个比给定数组长度大1的数组array，然后将给定数组中的元素复制到新数组的对应位置，接下来，它将currentSize设置为给定数组的长度，并调用buildHeap()方法构建堆。

public class MinPriorityQueue<T extends Comparable<T>> {
//最小优先队列
private static final int DEFAULT_CAPACITY = 10;//默认大小
private int currentSize;//当前堆的大小
private T[] array;//堆数组
public MinPriorityQueue() {
this.array = (T[]) new Comparable[DEFAULT_CAPACITY + 1];
currentSize = 0;
}
public MinPriorityQueue(int size) {
this.array = (T[]) new Comparable[size + 1];
currentSize = 0;
}
public MinPriorityQueue(T[] array) {
this.array = (T[]) new Comparable[array.length + 1];
for (int i = 0; i < array.length; i++) {
this.array[i + 1] = array[i];
}//从1开始算
currentSize = array.length;
buildHeap();
}
}

insert(T element): 往堆中插入元素。首先检查堆是否已满，如果堆已满，则抛出异常。然后将currentSize递增，将新元素放在数组的最后位置。接着通过将新元素与其父节点进行比较并交换的方式，使新元素上浮到正确的位置，以维持堆的性质。

/**
* 往堆中插入元素
*
* @param element 元素值
*/
public void insert(T element) {
try {
if (isFull()) {
throw new Exception("Array is full!");
}
int temp = ++currentSize;
array[temp] = element;//将element放在数组最后
while ((temp != 1) && (array[temp].compareTo(array[getParent(temp)]) < 0)) {
swap(array, temp, getParent(temp));
temp = getParent(temp);//如果比父结点的值小则于其交换
}//注意根结点的下标为1，不是0
} catch (Exception e) {
e.printStackTrace();
}
}

findMin(): 返回堆顶元素（最小值），即数组中的第一个元素array[1]。

deleteMin(): 删除堆顶元素。它首先检查堆是否为空，如果为空，则抛出异常。否则，它将堆顶元素与数组中最后一个元素进行交换，并将currentSize减1。然后，它通过将堆顶元素与其子节点进行比较并交换的方式，使堆顶元素下沉到正确的位置，以维持堆的性质。

public T findMin() {
return array[1];
}
/**
* 删除堆顶元素
*/
public void deleteMin() {
try {
if (isEmpty()) {
throw new Exception("Array is empty!");
} else {
swap(array, 1, currentSize--);//将堆顶元素放到最后,同时删除
if (currentSize != 0) siftDown(1);
}
} catch (Exception e) {
e.printStackTrace();
}
}

print(): 打印当前堆中的元素。

heapSort(): 对堆进行排序，并逐个输出排序结果。循环调用findMin()方法找到堆中的最小值并打印，然后调用deleteMin()方法删除堆顶元素，直到堆为空为止。

isEmpty(): 判断堆是否为空。如果currentSize为0，则堆为空，返回true；否则，返回false。

isFull(): 判断堆是否已满。如果currentSize等于数组长度减1，则堆已满，返回true；否则，返回false。

public void print() {
for (int i = 1; i <= currentSize; i++) {
System.out.print(array[i] + " ");
}
}
public void heapSort() {
while (currentSize != 0) {
System.out.print(findMin() + " ");
deleteMin();
}
}
public boolean isEmpty() {
return currentSize == 0;
}
public boolean isFull() {
return currentSize == array.length - 1;
}

siftDown(int pos):将给定位置pos的元素在堆中下沉到正确的位置，以维持堆的性质。

先检查给定位置pos是否合法，再用一个循环来判断当前位置pos是否为叶子节点。如果不是叶子节点，继续执行下面的操作；否则，循环结束。

在循环内部，方法首先获取当前位置pos的左子节点的索引j，即getLeft(pos)。然后，它检查当前位置pos是否有右子节点，并且右子节点的值比左子节点的值更小。如果满足条件，将右子节点的索引j更新为j+1，即取右子节点；方法比较当前位置pos的值和子节点array[j]的值。如果当前位置的值比子节点的值小，说明当前位置的值已经比子树中的值都小，不需要继续下沉，直接返回；如果当前位置的值比子节点的值大，说明当前位置的值需要下沉。方法调用swap(array, pos, j)交换当前位置pos和子节点array[j]的值，将当前位置的值下沉到子节点的位置；最后，将当前位置pos更新为子节点的位置j，继续下次循环，直到当前位置成为叶子节点为止。

/**
* 大的值下沉
*
* @param pos 当前位置
*/
private void siftDown(int pos) {
try {
if (pos < 0 || pos > currentSize) {
throw new Exception("Illegal position!");
}
while (!isLeaf(pos)) {
int j = getLeft(pos);
if ((j < currentSize) && (array[j].compareTo(array[j + 1])) > 0) j++;
//跟子树中最小的值交换
if (array[pos].compareTo(array[j]) < 0) return;
//当前值已经比子树中的值都小，则返回
swap(array, pos, j);//交换
pos = j;
}
} catch (Exception e) {
e.printStackTrace();
}
}

一些辅助的私有方法：

private boolean isLeaf(int i) {
return i > currentSize / 2;
}
private void buildHeap() {
for (int i = currentSize / 2; i > 0; i--) {
siftDown(i);//对每个非叶子结点进行下沉操作
//从右到左，从下到上
}
}
private int getLeft(int i) {
return 2 * i;
}
private int getRight(int i) {
return 2 * i + 1;
}
private int getParent(int i) {
return i / 2;
}
private void swap(T[] array, int x, int y) {
T temp = array[y];
array[y] = array[x];
array[x] = temp;
}

测试一下：

public static void main(String[] args) throws Exception {
Edge edge1 = new Edge(1, 2, 1);
Edge edge2 = new Edge(1, 2, 2);
Edge edge3 = new Edge(1, 2, 6);
Edge edge4 = new Edge(1, 2, 4);
Edge edge5 = new Edge(1, 2, 5);
Edge edge6 = new Edge(1, 2, 7);
Edge edge7 = new Edge(1, 2, 3);
// Integer[] elements = {1, 2, 6, 4, 5, 7, 3};
// MinPriorityQueue<Integer> test = new MinPriorityQueue<Integer>(elements);
Edge[] edges = {edge1, edge2, edge3, edge4, edge5, edge6, edge7};
MinPriorityQueue<Edge> test = new MinPriorityQueue<Edge>(edges);
test.print();
System.out.println();
test.heapSort();
System.out.println();
test.print();
}

结果如下：

图6 最小优先队列测试结果

Graph2：

不再详细讲解，只列出深度优先搜索和广度优先搜索。

public void DFS() {
for (int i = 0; i < getVertexNum(); i++) {
setMark(i, UNVISITED);
}//初始化所有顶点
for (int i = 0; i < getVertexNum(); i++) {
if (getMark(i) == UNVISITED) {
DFSHelp(i);
}
}
}
public void DFSHelp(int v) {
System.out.print(V.get(v) + " ");
setMark(v, VISITED);
for (int edge = getFirst(v); isEdge(v, edge); edge = getNext(v, edge)) {
if (getMark(edge) == UNVISITED) {
DFSHelp(edge);
}
}
}
public void BFS() {
for (int i = 0; i < getVertexNum(); i++) {
setMark(i, UNVISITED);
}//初始化所有顶点
for (int i = 0; i < getVertexNum(); i++) {
if (getMark(i) == UNVISITED) {
BFSHelp(i);
}
}
}
public void BFSHelp(int v) {
LQueue<Integer> queue = new LQueue<>();
queue.enqueue(v);
setMark(v, VISITED);
while (!queue.isEmpty()) {
int temp = queue.dequeue();
System.out.print(V.get(temp) + " ");
for (int index = getFirst(temp); isEdge(temp, index); index = getNext(temp, index)) {
if (getMark(index) == UNVISITED) {
queue.enqueue(index);
setMark(index, VISITED);
}
}
}
}

测试一下：

public static void main(String[] args) {
//定义图的所有顶点
String[] vertexs = {"A", "B", "C", "D", "E", "F"};
//创建图
GraphM2 graph = new GraphM2(vertexs.length);
//添加顶点到图中
for (String vertex : vertexs) {
graph.insertVertex(vertex);
}
//添加边到图中
graph.insertEdge(0, 2, 1);
graph.insertEdge(0, 4, 1);
graph.insertEdge(1, 2, 1);
graph.insertEdge(1, 5, 1);
graph.insertEdge(2, 3, 1);
graph.insertEdge(2, 5, 1);
graph.insertEdge(3, 5, 1);
graph.insertEdge(4, 5, 1);
graph.print();
graph.DFS();
System.out.println();
graph.BFS();
}

结果如下：

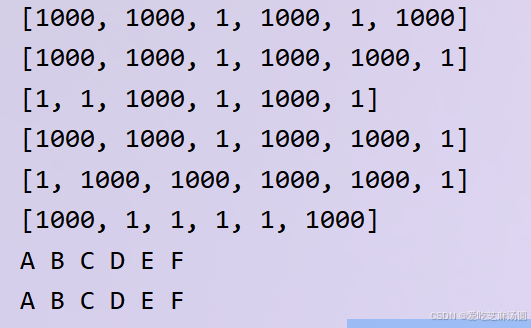
图6 图测试结果

队列LQueue：

package homework02;
import java.util.NoSuchElementException;
public class LQueue<T> {
private Node<T> front;
private Node<T> rear;
private class Node<T> {
private T data;
private Node<T> next;
public Node(T data) {
this.data = data;
this.next = null;
}
}
public LQueue() {
front = null;
rear = null;
}
public boolean isEmpty() {
return front == null;
}
public void enqueue(T item) {
Node<T> newNode = new Node<>(item);
if (isEmpty()) {
front = newNode;
rear = newNode;
} else {
rear.next = newNode;
rear = newNode;
}
}
public T dequeue() {
if (isEmpty()) {
throw new NoSuchElementException("Queue is empty");
}
T data = front.data;
front = front.next;
if (front == null) {
rear = null;
}
return data;
}
public T peek() {
if (isEmpty()) {
throw new NoSuchElementException("Queue is empty");
}
return front.data;
}
}

边Edge：

package homework02;
import org.jetbrains.annotations.NotNull;
//这个类的目的就是为了Kruskal算法中的优先队列创建的
public class Edge implements Comparable<Edge> {
private int v1;//起点
private int v2;//终点
private int weight;//权重
public Edge(int v1, int v2) {
this.v1 = v1;
this.v2 = v2;
}
public Edge(int v1, int v2, int weight) {
this.v1 = v1;
this.v2 = v2;
this.weight = weight;
}
public int getV1() {
return v1;
}
public void setV1(int v1) {
this.v1 = v1;
}
public int getV2() {
return v2;
}
public void setV2(int v2) {
this.v2 = v2;
}
public int getWeight() {
return weight;
}
public void setWeight(int weight) {
this.weight = weight;
}
@Override
public int compareTo(@NotNull Edge edge) {
return Integer.compare(this.weight, edge.weight);
}
@Override
public String toString() {
return "Edge{" +
v1 +
"->" + v2 +
" weight=" + weight +
'}';
}
}

算法设计

Kruskal算法算法步骤：

1.设连通网 N = (V, E )，令最小生成树初始状态为只有 n 个顶点而无边的非连通图 T=(V, { })，每个顶点自成一个连通分量。

3.依此类推，直至 T 中所有顶点都在同一连通分量上为止。

public class Kruskal {
private ArrayList<Edge> MST;//最小生成树中的所有边
private UnionFindTree ufTree;//并查集树，放索引
private MinPriorityQueue<Edge> allEdges;//图中所有的边
private GraphM2 originalGraph;//用相邻矩阵实现的原图
private int vertexNum;//结点数
private GraphM2 newGraph;//用相邻矩阵实现的新图
public Kruskal(GraphM2 originalGraph) {
this.originalGraph = originalGraph;
this.vertexNum = originalGraph.getVertexNum();
}
public void generateMST() {
this.MST = new ArrayList<Edge>();//初始化MST
Node[] nodes = new Node[vertexNum];
for (int i = 0; i < vertexNum; i++) {
nodes[i] = new Node(i);
}
this.ufTree = new UnionFindTree(nodes);//初始化并查集
this.allEdges = new MinPriorityQueue<>(originalGraph.getEdgeNum());//初始化优先队列
//把图中的边放到储存边的最小优先队列中，目的是为了快速检索
for (int i = 0; i < vertexNum; i++) {
for (int j = i + 1; j < vertexNum; j++) {
if (originalGraph.getWeight(i, j) != GraphM2.UNCONNECTED) {
allEdges.insert(new Edge(i, j, originalGraph.getWeight(i, j)));
}
}
}
while (!allEdges.isEmpty() && MST.size() < vertexNum - 1) {
Edge e = allEdges.findMin();
allEdges.deleteMin();
int v1 = e.getV1();
int v2 = e.getV2();
//判断v1和v2是否已经连通
if (ufTree.isConnected(v1, v2)) continue;
ufTree.union(v1, v2);//不连通则连接
MST.add(e);//将边并入MST
}
}
public ArrayList<Edge> getMST() {
return MST;
}
}

这样我们就得到了MST，那么我们还需要作图以及求解路径，我们只需得到down，right，matrix三个矩阵，我们就能根据第一问的算法绘图以及求解路径。下面是得到三个二维数组的方法。

public int[][] getMatrix(){
newGraph = new GraphM2(Constants.GRID_SIZE * Constants.GRID_SIZE);
for (Edge edge : MST){
int cell1 = Integer.parseInt(originalGraph.getVertexValue(edge.getV1()));
int cell2 = Integer.parseInt(originalGraph.getVertexValue(edge.getV2()));
newGraph.insertEdge(cell1,cell2,1);
}
return newGraph.getMatrix();
}
public int[][] getDown(){
//把down所有数都写为1000
int[][] down = new int[Constants.GRID_SIZE][Constants.GRID_SIZE];
for (int i = 0; i < Constants.GRID_SIZE; i++) {
for (int j = 0; j < Constants.GRID_SIZE; j++) {
down[i][j] = Constants.INNEIGHBOURING;
}
}
for (Edge edge : MST){
int cell1 = Integer.parseInt(originalGraph.getVertexValue(edge.getV1()));
int cell2 = Integer.parseInt(originalGraph.getVertexValue(edge.getV2()));
//保证cell1小于cell2
if(cell1 > cell2){
int temp = cell1;
cell1 = cell2;
cell2 = temp;
}
//保证同一列，将上边cell1格子的写为1
if(getCol(cell1) == getCol(cell2)){
down[getRow(cell1)][getCol(cell1)] = 1;
}
}
return down;
}
public int[][] getRight(){
//把right所有数都写为1000
int[][] right = new int[Constants.GRID_SIZE][Constants.GRID_SIZE];
for (int i = 0; i < Constants.GRID_SIZE; i++) {
for (int j = 0; j < Constants.GRID_SIZE; j++) {
right[i][j] = Constants.INNEIGHBOURING;
}
}
for (Edge edge : MST){
int cell1 = Integer.parseInt(originalGraph.getVertexValue(edge.getV1()));
int cell2 = Integer.parseInt(originalGraph.getVertexValue(edge.getV2()));
//保证cell1小于cell2
if(cell1 > cell2){
int temp = cell1;
cell1 = cell2;
cell2 = temp;
}
//保证同一行，将左边cell1格子的写为1
if(getRow(cell1) == getRow(cell2)){
right[getRow(cell1)][getCol(cell1)] = 1;
}
}
return right;
}

这样我们就可以调用这三个方法得到三个矩阵，再调用第一问的方法进行绘图，求解路径，绘制路径。

下面是Test2类：

首先调用方法得到三个矩阵。

public class Test2 extends JPanel {
public GraphM2 graph;
public int padding = Constants.PADDING;
public int width = (Constants.WIDTH - Constants.PADDING - Constants.PADDING) / Constants.GRID_SIZE;
public Cell[][] maze;
public int [][] down;
public int [][] right;
public int [][] matrix;
public List<Integer> path;
public Puzzle puzzle = new Puzzle();
public Test2() {
maze = new Cell[Constants.GRID_SIZE][Constants.GRID_SIZE];
helpTest();
}
public void helpTest(){
//创建抽象的全连接的图
//定义图的所有顶点
Integer[] vertexs = new Integer[Constants.GRID_SIZE * Constants.GRID_SIZE];
for (int i = 0; i < vertexs.length; i++) {
vertexs[i] = i;
}
//创建图并把顶点放在图中
graph = new GraphM2(vertexs.length);
for (Integer vertex : vertexs) {
graph.insertVertex(vertex);
}
//添加随机边到图中
Random r = new Random();
for (int i = 0; i < Constants.GRID_SIZE - 1; i++) {
for (int j = 0; j < Constants.GRID_SIZE; j++) {
graph.insertEdge(i * Constants.GRID_SIZE + j, (i + 1) * Constants.GRID_SIZE + j, r.nextInt(300));
}
}
for (int i = 0; i < Constants.GRID_SIZE; i++) {
for (int j = 0; j < Constants.GRID_SIZE - 1; j++) {
graph.insertEdge(i * Constants.GRID_SIZE + j, i * Constants.GRID_SIZE + j + 1, r.nextInt(300));
}
}
//调用Kruskal 算法对步骤 1 中的图生成最小支撑树
Kruskal kruskal = new Kruskal(graph);
kruskal.generateMST();
//得到down和right数组
down = kruskal.getDown();
right = kruskal.getRight();
matrix = kruskal.getMatrix();
path = puzzle.getPath(matrix);
}
}

进行绘图：

//这是个自动调用的方法，必须设置为public
public void paintComponent(Graphics g) {
super.paintComponent(g);
// 画NUM*NUM条黑线
for (int i = 0; i <= Constants.GRID_SIZE; i++) {
g.drawLine(padding + i * width, padding, padding + i * width,
padding + Constants.GRID_SIZE * width);
}
for (int j = 0; j <= Constants.GRID_SIZE; j++) {
g.drawLine(padding, padding + j * width, padding + Constants.GRID_SIZE * width,
padding + j * width);
}
// 使用背景色，在有路径的格子之间画边，把墙抹掉
g.setColor(this.getBackground());
//根据Puzzle中的数组进行抹边
for (int i = 0; i < Constants.GRID_SIZE; i++) {
for (int j = 0; j < Constants.GRID_SIZE; j++) {
maze[i][j] = new Cell(i, j);
if (down[i][j] == Constants.NEIGHBOURING) {
maze[i][j].setDown(Constants.NEIGHBOURING);
}
if (down[i][j] == Constants.INNEIGHBOURING) {
maze[i][j].setDown(Constants.INNEIGHBOURING);
}
if (right[i][j] == Constants.NEIGHBOURING) {
maze[i][j].setRight(Constants.NEIGHBOURING);
}
if (right[i][j] == Constants.INNEIGHBOURING) {
maze[i][j].setRight(Constants.INNEIGHBOURING);
}
}
}
for (int i = Constants.GRID_SIZE - 1; i >= 0; i--) {
for (int j = Constants.GRID_SIZE - 1; j >= 0; j--) {
if (maze[i][j].getRight() == Constants.NEIGHBOURING) {
clearFence(i, j, i, j + 1, g);
}
if (maze[i][j].getDown() == Constants.NEIGHBOURING) {
clearFence(i, j, i + 1, j, g);
}
}
}
// 画左上角的入口
g.drawLine(padding, padding + 1, padding, padding + width - 1);
int last = padding + Constants.GRID_SIZE * width;
// 画右下角出口
g.drawLine(last, last - 1, last, last - width + 1);
// 画下边框
g.setColor(Color.BLACK);
g.drawLine(padding, last, last, last);
// 画右边框
g.drawLine(last, padding, last, last - width);
// 画路径
drawPath(g);
}
// 私有方法，目的是抹掉两个格子之间的边
private void clearFence(int i, int j, int fx, int fy, Graphics g) {
int sx = padding + ((j > fy ? j : fy) * width),
sy = padding + ((i > fx ? i : fx) * width),
dx = (i == fx ? sx : sx + width),
dy = (i == fx ? sy + width : sy);
if (sx != dx) {
sx++;
dx--;
} else {
sy++;
dy--;
}
g.drawLine(sx, sy, dx, dy);
}
// 由格子的行数列数，得到格子中心点的像素XY坐标
private int getCenterX(Cell p) {
return padding + p.getY() * width + width / 2;
}
private int getCenterY(Cell p) {
return padding + p.getX() * width + width / 2;
}
// 由序列数得到对应的行和列
private int getRow(int num) {
return (num ) / Constants.GRID_SIZE;
}
private int getCol(int num) {
return num % Constants.GRID_SIZE;
}
private void drawPath(Graphics g) {
g.setColor(Color.red);
// 已经得到初始路径到最后路径的list，接下来对照相应的格子，再画出来就行
for (int i = 0; i < path.size() - 1; i++) {
int first = path.get(i);
int second = path.get(i + 1);
g.drawLine(getCenterX(maze[getRow(first)][getCol(first)]), getCenterY(maze[getRow(first)][getCol(first)]), getCenterX(maze[getRow(second)][getCol(second)]), getCenterY(maze[getRow(second)][getCol(second)]));
}
}

进行测试：

public static void main(String[] args) {
JPanel test2 = new Test2();
JFrame frame = new JFrame("homework02.Maze");
//下面一行自动调用paintComponent方法
frame.setContentPane(test2);
frame.setSize(Constants.WIDTH + Constants.PADDING, Constants.WIDTH + Constants.PADDING + Constants.PADDING);
frame.setLocation(Constants.LX, Constants.LY);
frame.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);
frame.setVisible(true);
}

运行结果展示

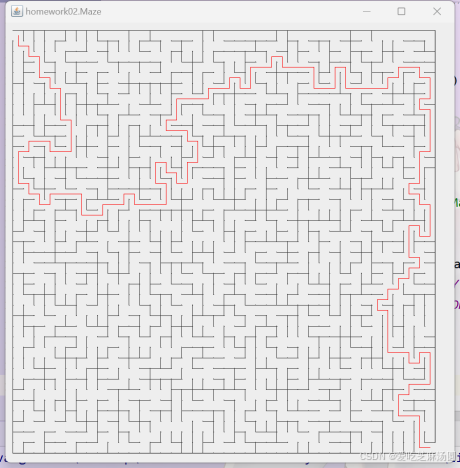
图7 测试结果

总结和收获

复习了很多数据结构和算法，包括最小优先队列，堆排序，队列，最小支撑树，用Kruskal 算法，并查集树等等，收获很大。

附录：

任务2

UnionFindTree：

package homework02;
public class UnionFindTree {
//用树实现并查集
public Node[] set;
public UnionFindTree(Node[] set) {
this.set = set;
}
/**
* 返回包含给定元素的集合名字
*
* @param i 元素下标
* @return 以根结点下标作为集合名字
*/
public int find(int i) {
//使用路劲压缩法：在查找某个元素是否属于某个集合时，将该结点到根结点路径上
// 所有结点的父指针全部改为指向根结点，这种方式可以产生极浅的树
Node current = set[i];
if (current.getParent()<0)
return i;
return current.setParent(find(current.getParent()));
}
/**
* 生成一个新的集合，该集合是i所属的集合set1和j所属的集合set2的并集
*
* @param i
* @param j
*/
public void union(int i, int j) {
//使用重量平衡原则
int root1 = find(i);
int num1 = set[root1].getParent();
int root2 = find(j);
int num2 = set[root2].getParent();
if (num1 <= num2) {
set[root1].setParent(num1+num2);
set[root2].setParent(root1);
//将其中结点数少的一棵树的根结点的父结点设置为
//结点数多的一棵树的根结点
} else {
set[root2].setParent(num1+num2);
set[root1].setParent(root2);
//将其中结点数少的一棵树的根结点的父结点设置为
//结点数多的一棵树的根结点
}
}
/**
* 判断元素i和元素j是否在同一个分组中
* @param i
* @param j
* @return
*/
public boolean isConnected(int i,int j){
return find(i)==find(j);
}
public void print() {
for (int i = 0; i < set.length; i++) {
System.out.print(set[i].getElement() + " ");
}
}
public static void main(String[] args) {
// 创建一组元素，共有8个元素
Node[] set = new Node[8];
for (int i = 0; i < set.length; i++) {
set[i] = new Node(i, -1); // 初始时每个元素都是一个独立的集合，父节点为-1
}
UnionFindTree unionFind = new UnionFindTree(set);
// 合并一些集合
unionFind.union(0, 1);
unionFind.union(2, 3);
unionFind.union(4, 5);
unionFind.union(6, 7);
unionFind.union(0, 2);
unionFind.union(4, 6);
unionFind.union(0, 4);
// 验证元素之间的连通性
System.out.println("0 和 7 是否连通？" + unionFind.isConnected(0, 7));
System.out.println("1 和 3 是否连通？" + unionFind.isConnected(1, 3));
System.out.println("2 和 6 是否连通？" + unionFind.isConnected(2, 6));
System.out.println("4 和 5 是否连通？" + unionFind.isConnected(4, 5));
// 打印并查集中的元素
unionFind.print();
}
}

MinPriorityQueue：

package homework02;
public class MinPriorityQueue<T extends Comparable<T>> {
//最小优先队列
private static final int DEFAULT_CAPACITY = 10;//默认大小
private int currentSize;//当前堆的大小
private T[] array;//堆数组
public MinPriorityQueue() {
this.array = (T[]) new Comparable[DEFAULT_CAPACITY + 1];
currentSize = 0;
}
public MinPriorityQueue(int size) {
this.array = (T[]) new Comparable[size + 1];
currentSize = 0;
}
public MinPriorityQueue(T[] array) {
this.array = (T[]) new Comparable[array.length + 1];
for (int i = 0; i < array.length; i++) {
this.array[i + 1] = array[i];
}//从1开始算
currentSize = array.length;
buildHeap();
}
/**
* 往堆中插入元素
*
* @param element 元素值
*/
public void insert(T element) {
try {
if (isFull()) {
throw new Exception("Array is full!");
}
int temp = ++currentSize;
array[temp] = element;//将element放在数组最后
while ((temp != 1) && (array[temp].compareTo(array[getParent(temp)]) < 0)) {
swap(array, temp, getParent(temp));
temp = getParent(temp);//如果比父结点的值小则于其交换
}//注意根结点的下标为1，不是0
} catch (Exception e) {
e.printStackTrace();
}
}
public T findMin() {
return array[1];
}
/**
* 删除堆顶元素
*/
public void deleteMin() {
try {
if (isEmpty()) {
throw new Exception("Array is empty!");
} else {
swap(array, 1, currentSize--);//将堆顶元素放到最后,同时删除
if (currentSize != 0) siftDown(1);
}
} catch (Exception e) {
e.printStackTrace();
}
}
/**
* 大的值下沉
*
* @param pos 当前位置
*/
private void siftDown(int pos) {
try {
if (pos < 0 || pos > currentSize) {
throw new Exception("Illegal position!");
}
while (!isLeaf(pos)) {
int j = getLeft(pos);
if ((j < currentSize) && (array[j].compareTo(array[j + 1])) > 0) j++;
//跟子树中最小的值交换
if (array[pos].compareTo(array[j]) < 0) return;
//当前值已经比子树中的值都小，则返回
swap(array, pos, j);//交换
pos = j;
}
} catch (Exception e) {
e.printStackTrace();
}
}
public void print() {
for (int i = 1; i <= currentSize; i++) {
System.out.print(array[i] + " ");
}
}
public void heapSort() {
while (currentSize != 0) {
System.out.print(findMin() + " ");
deleteMin();
}
}
public boolean isEmpty() {
return currentSize == 0;
}
public boolean isFull() {
return currentSize == array.length - 1;
}
private boolean isLeaf(int i) {
return i > currentSize / 2;
}
private void buildHeap() {
for (int i = currentSize / 2; i > 0; i--) {
siftDown(i);//对每个非叶子结点进行下沉操作
//从右到左，从下到上
}
}
private int getLeft(int i) {
return 2 * i;
}
private int getRight(int i) {
return 2 * i + 1;
}
private int getParent(int i) {
return i / 2;
}
private void swap(T[] array, int x, int y) {
T temp = array[y];
array[y] = array[x];
array[x] = temp;
}
public static void main(String[] args) throws Exception {
Edge edge1 = new Edge(1, 2, 1);
Edge edge2 = new Edge(1, 2, 2);
Edge edge3 = new Edge(1, 2, 6);
Edge edge4 = new Edge(1, 2, 4);
Edge edge5 = new Edge(1, 2, 5);
Edge edge6 = new Edge(1, 2, 7);
Edge edge7 = new Edge(1, 2, 3);
// Integer[] elements = {1, 2, 6, 4, 5, 7, 3};
// MinPriorityQueue<Integer> test = new MinPriorityQueue<Integer>(elements);
Edge[] edges = {edge1, edge2, edge3, edge4, edge5, edge6, edge7};
MinPriorityQueue<Edge> test = new MinPriorityQueue<Edge>(edges);
test.print();
System.out.println();
test.heapSort();
System.out.println();
test.print();
}
}

GraphM2：

package homework02;
import homework01.GraphM1;
import java.util.ArrayList;
import java.util.Arrays;
public class GraphM2 extends GraphM1 {
//用相邻矩阵实现无向图
private ArrayList<String> V;//顶点
private int E;//边数
private int[][] matrix;//相邻矩阵
private int[] mark;//判定一个结点是否被访问过
public static final int VISITED = -2;//已经访问
public static final int UNVISITED = -3;//未访问
public static final int UNCONNECTED = 1000;//未访问
public GraphM2() {
}
/**
* 初始化无向图
*
* @param n 结点数
*/
public GraphM2(int n) {
matrix = new int[n][n];
mark = new int[n];
for (int i = 0; i < n; i++) {
mark[i] = UNVISITED;
for (int j = 0; j < n; j++) {
matrix[i][j] = UNCONNECTED;
}
}
V = new ArrayList<String>(n);
}
public int[][] getMatrix() {
return matrix;
}
/**
* 添加结点
*
* @param vertex 结点值
*/
public void insertVertex(String vertex) {
V.add(vertex);
}
public void insertVertex(Integer vertex) {
V.add(String.valueOf(vertex));
}
/**
* 插入边
*
* @param v1 起点下标
* @param v2 终点下标
* @param weight 权值，这里0表示不相邻，1表示相邻
*/
public void insertEdge(int v1, int v2, int weight) {
matrix[v1][v2] = weight;
matrix[v2][v1] = weight;
E++;//边数+1
}
/**
* 获得v1->v2的权值
*
* @param v1
* @param v2
* @return
*/
public int getWeight(int v1, int v2) {
return matrix[v1][v2];
}
/**
* 获得边的数量
*
* @return
*/
public int getEdgeNum() {
return E;
}
/**
* 获得结点数
*
* @return
*/
public int getVertexNum() {
return V.size();
}
public String getVertexValue(int index) {
return V.get(index);
}
/**
* 获得某个结点的第一个邻接点下标
*
* @param v 某个顶点下标
* @return 第一个邻接点下标
*/
public int getFirst(int v) {
for (int i = 0; i < V.size(); i++) {
if (matrix[v][i] > 0) {
return i;
}
}
return -1;
}
/**
* @param v1 某个顶点坐标
* @param v2 前一个邻接结点坐标
* @return 下一个邻接结点坐标
*/
public int getNext(int v1, int v2) {
for (int i = v2 + 1; i < V.size(); i++) {
if (matrix[v1][i] > 0) {
return i;
}
}
return -1;
}
public boolean isEdge(int v1, int v2) {
return isLegalIndex(v1) && isLegalIndex(v2) && matrix[v1][v2] > 0;
}
public boolean isLegalIndex(int v) {
return v >= 0 && v < V.size();
}
public void DFS() {
for (int i = 0; i < getVertexNum(); i++) {
setMark(i, UNVISITED);
}//初始化所有顶点
for (int i = 0; i < getVertexNum(); i++) {
if (getMark(i) == UNVISITED) {
DFSHelp(i);
}
}
}
public void DFSHelp(int v) {
System.out.print(V.get(v) + " ");
setMark(v, VISITED);
for (int edge = getFirst(v); isEdge(v, edge); edge = getNext(v, edge)) {
if (getMark(edge) == UNVISITED) {
DFSHelp(edge);
}
}
}
public void BFS() {
for (int i = 0; i < getVertexNum(); i++) {
setMark(i, UNVISITED);
}//初始化所有顶点
for (int i = 0; i < getVertexNum(); i++) {
if (getMark(i) == UNVISITED) {
BFSHelp(i);
}
}
}
public void BFSHelp(int v) {
LQueue<Integer> queue = new LQueue<>();
queue.enqueue(v);
setMark(v, VISITED);
while (!queue.isEmpty()) {
int temp = queue.dequeue();
System.out.print(V.get(temp) + " ");
for (int index = getFirst(temp); isEdge(temp, index); index = getNext(temp, index)) {
if (getMark(index) == UNVISITED) {
queue.enqueue(index);
setMark(index, VISITED);
}
}
}
}
public void setMark(int v, int val) {
mark[v] = val;
}
public int getMark(int v) {
return mark[v];
}
//打印邻接矩阵
public void print() {
for (int[] edge : matrix) {
System.out.println(Arrays.toString(edge));
}
}
public static void main(String[] args) {
//定义图的所有顶点
String[] vertexs = {"A", "B", "C", "D", "E", "F"};
//创建图
GraphM2 graph = new GraphM2(vertexs.length);
//添加顶点到图中
for (String vertex : vertexs) {
graph.insertVertex(vertex);
}
//添加边到图中
graph.insertEdge(0, 2, 1);
graph.insertEdge(0, 4, 1);
graph.insertEdge(1, 2, 1);
graph.insertEdge(1, 5, 1);
graph.insertEdge(2, 3, 1);
graph.insertEdge(2, 5, 1);
graph.insertEdge(3, 5, 1);
graph.insertEdge(4, 5, 1);
graph.print();
graph.DFS();
System.out.println();
graph.BFS();
}
}

LQueue：

package homework02;
import java.util.NoSuchElementException;
public class LQueue<T> {
private Node<T> front;
private Node<T> rear;
private class Node<T> {
private T data;
private Node<T> next;
public Node(T data) {
this.data = data;
this.next = null;
}
}
public LQueue() {
front = null;
rear = null;
}
public boolean isEmpty() {
return front == null;
}
public void enqueue(T item) {
Node<T> newNode = new Node<>(item);
if (isEmpty()) {
front = newNode;
rear = newNode;
} else {
rear.next = newNode;
rear = newNode;
}
}
public T dequeue() {
if (isEmpty()) {
throw new NoSuchElementException("Queue is empty");
}
T data = front.data;
front = front.next;
if (front == null) {
rear = null;
}
return data;
}
public T peek() {
if (isEmpty()) {
throw new NoSuchElementException("Queue is empty");
}
return front.data;
}
}

Node：

package homework02;
public class Node {
private int parent;//父结点下标
private Object element;//存储元素内容
public Node() {
this(null, -1);
}
public Node(Object element) {
this(element, -1);
}
public Node(Object element, int parent) {
this.element = element;
this.parent = parent;
}
public int getParent() {
return parent;
}
public int setParent(int parent) {
return this.parent = parent;
}
public Object getElement() {
return element;
}
public void setElement(Object element) {
this.element = element;
}
}

Edge：

package homework02;
import org.jetbrains.annotations.NotNull;
//这个类的目的就是为了Kruskal算法中的优先队列创建的
public class Edge implements Comparable<Edge> {
private int v1;//起点
private int v2;//终点
private int weight;//权重
public Edge(int v1, int v2) {
this.v1 = v1;
this.v2 = v2;
}
public Edge(int v1, int v2, int weight) {
this.v1 = v1;
this.v2 = v2;
this.weight = weight;
}
public int getV1() {
return v1;
}
public void setV1(int v1) {
this.v1 = v1;
}
public int getV2() {
return v2;
}
public void setV2(int v2) {
this.v2 = v2;
}
public int getWeight() {
return weight;
}
public void setWeight(int weight) {
this.weight = weight;
}
@Override
public int compareTo(@NotNull Edge edge) {
return Integer.compare(this.weight, edge.weight);
}
@Override
public String toString() {
return "Edge{" +
v1 +
"->" + v2 +
" weight=" + weight +
'}';
}
}

Kruskal：

package homework02;
import java.util.ArrayList;
import homework01.*;
public class Kruskal {
private ArrayList<Edge> MST;//最小生成树中的所有边
private UnionFindTree ufTree;//并查集树，放索引
private MinPriorityQueue<Edge> allEdges;//图中所有的边
private GraphM2 originalGraph;//用相邻矩阵实现的原图
private int vertexNum;//结点数
private GraphM2 newGraph;//用相邻矩阵实现的新图
public Kruskal(GraphM2 originalGraph) {
this.originalGraph = originalGraph;
this.vertexNum = originalGraph.getVertexNum();
}
public void generateMST() {
this.MST = new ArrayList<Edge>();//初始化MST
Node[] nodes = new Node[vertexNum];
for (int i = 0; i < vertexNum; i++) {
nodes[i] = new Node(i);
}
this.ufTree = new UnionFindTree(nodes);//初始化并查集
this.allEdges = new MinPriorityQueue<>(originalGraph.getEdgeNum());//初始化优先队列
//把图中的边放到储存边的最小优先队列中，目的是为了快速检索
for (int i = 0; i < vertexNum; i++) {
for (int j = i + 1; j < vertexNum; j++) {
if (originalGraph.getWeight(i, j) != GraphM2.UNCONNECTED) {
allEdges.insert(new Edge(i, j, originalGraph.getWeight(i, j)));
}
}
}
while (!allEdges.isEmpty() && MST.size() < vertexNum - 1) {
Edge e = allEdges.findMin();
allEdges.deleteMin();
int v1 = e.getV1();
int v2 = e.getV2();
//判断v1和v2是否已经连通
if (ufTree.isConnected(v1, v2)) continue;
ufTree.union(v1, v2);//不连通则连接
MST.add(e);//将边并入MST
}
}
public ArrayList<Edge> getMST() {
return MST;
}
// 由序列数得到对应的行和列
private int getRow(int num) {
return num / Constants.GRID_SIZE;
}
private int getCol(int num) {
return num % Constants.GRID_SIZE;
}
public int[][] getMatrix(){
newGraph = new GraphM2(Constants.GRID_SIZE * Constants.GRID_SIZE);
for (Edge edge : MST){
int cell1 = Integer.parseInt(originalGraph.getVertexValue(edge.getV1()));
int cell2 = Integer.parseInt(originalGraph.getVertexValue(edge.getV2()));
newGraph.insertEdge(cell1,cell2,1);
}
return newGraph.getMatrix();
}
public int[][] getDown(){
//把down所有数都写为1000
int[][] down = new int[Constants.GRID_SIZE][Constants.GRID_SIZE];
for (int i = 0; i < Constants.GRID_SIZE; i++) {
for (int j = 0; j < Constants.GRID_SIZE; j++) {
down[i][j] = Constants.INNEIGHBOURING;
}
}
for (Edge edge : MST){
int cell1 = Integer.parseInt(originalGraph.getVertexValue(edge.getV1()));
int cell2 = Integer.parseInt(originalGraph.getVertexValue(edge.getV2()));
//保证cell1小于cell2
if(cell1 > cell2){
int temp = cell1;
cell1 = cell2;
cell2 = temp;
}
//保证同一列，将上边cell1格子的写为1
if(getCol(cell1) == getCol(cell2)){
down[getRow(cell1)][getCol(cell1)] = 1;
}
}
return down;
}
public int[][] getRight(){
//把right所有数都写为1000
int[][] right = new int[Constants.GRID_SIZE][Constants.GRID_SIZE];
for (int i = 0; i < Constants.GRID_SIZE; i++) {
for (int j = 0; j < Constants.GRID_SIZE; j++) {
right[i][j] = Constants.INNEIGHBOURING;
}
}
for (Edge edge : MST){
int cell1 = Integer.parseInt(originalGraph.getVertexValue(edge.getV1()));
int cell2 = Integer.parseInt(originalGraph.getVertexValue(edge.getV2()));
//保证cell1小于cell2
if(cell1 > cell2){
int temp = cell1;
cell1 = cell2;
cell2 = temp;
}
//保证同一行，将左边cell1格子的写为1
if(getRow(cell1) == getRow(cell2)){
right[getRow(cell1)][getCol(cell1)] = 1;
}
}
return right;
}
/**
* 打印MST的所有边
*/
public void printMST() {
for (Edge edge : MST) {
System.out.println(originalGraph.getVertexValue(edge.getV1()) + "-"
+ originalGraph.getWeight(edge.getV1(), edge.getV2())
+ "->" + originalGraph.getVertexValue(edge.getV2()));
}
}
public static void main(String[] args) {
String[] vertexs = {"A", "B", "C", "D", "E", "F"};
//创建图
GraphM2 graph = new GraphM2(vertexs.length);
//添加顶点到图中
for (String vertex : vertexs) {
graph.insertVertex(vertex);
}
//添加边到图中
graph.insertEdge(0, 2, 7);
graph.insertEdge(0, 4, 9);
graph.insertEdge(1, 2, 5);
graph.insertEdge(1, 5, 6);
graph.insertEdge(2, 3, 1);
graph.insertEdge(2, 5, 2);
graph.insertEdge(3, 5, 2);
graph.insertEdge(4, 5, 1);
Kruskal test = new Kruskal(graph);
test.generateMST();
test.printMST();
}
}

Test2：

package homework02;
import homework01.*;
import javax.swing.*;
import java.awt.*;
import java.util.List;
import java.util.Random;
public class Test2 extends JPanel {
public GraphM2 graph;
public int padding = Constants.PADDING;
public int width = (Constants.WIDTH - Constants.PADDING - Constants.PADDING) / Constants.GRID_SIZE;
public Cell[][] maze;
public int [][] down;
public int [][] right;
public int [][] matrix;
public List<Integer> path;
public Puzzle puzzle = new Puzzle();
public Test2() {
maze = new Cell[Constants.GRID_SIZE][Constants.GRID_SIZE];
helpTest();
}
public void helpTest(){
//创建抽象的全连接的图
//定义图的所有顶点
Integer[] vertexs = new Integer[Constants.GRID_SIZE * Constants.GRID_SIZE];
for (int i = 0; i < vertexs.length; i++) {
vertexs[i] = i;
}
//创建图并把顶点放在图中
graph = new GraphM2(vertexs.length);
for (Integer vertex : vertexs) {
graph.insertVertex(vertex);
}
//添加随机边到图中
Random r = new Random();
for (int i = 0; i < Constants.GRID_SIZE - 1; i++) {
for (int j = 0; j < Constants.GRID_SIZE; j++) {
graph.insertEdge(i * Constants.GRID_SIZE + j, (i + 1) * Constants.GRID_SIZE + j, r.nextInt(300));
}
}
for (int i = 0; i < Constants.GRID_SIZE; i++) {
for (int j = 0; j < Constants.GRID_SIZE - 1; j++) {
graph.insertEdge(i * Constants.GRID_SIZE + j, i * Constants.GRID_SIZE + j + 1, r.nextInt(300));
}
}
//调用Kruskal 算法对步骤 1 中的图生成最小支撑树
Kruskal kruskal = new Kruskal(graph);
kruskal.generateMST();
//得到down和right数组
down = kruskal.getDown();
right = kruskal.getRight();
matrix = kruskal.getMatrix();
path = puzzle.getPath(matrix);
}
//这是个自动调用的方法，必须设置为public
public void paintComponent(Graphics g) {
super.paintComponent(g);
// 画NUM*NUM条黑线
for (int i = 0; i <= Constants.GRID_SIZE; i++) {
g.drawLine(padding + i * width, padding, padding + i * width,
padding + Constants.GRID_SIZE * width);
}
for (int j = 0; j <= Constants.GRID_SIZE; j++) {
g.drawLine(padding, padding + j * width, padding + Constants.GRID_SIZE * width,
padding + j * width);
}
// 使用背景色，在有路径的格子之间画边，把墙抹掉
g.setColor(this.getBackground());
//根据Puzzle中的数组进行抹边
for (int i = 0; i < Constants.GRID_SIZE; i++) {
for (int j = 0; j < Constants.GRID_SIZE; j++) {
maze[i][j] = new Cell(i, j);
if (down[i][j] == Constants.NEIGHBOURING) {
maze[i][j].setDown(Constants.NEIGHBOURING);
}
if (down[i][j] == Constants.INNEIGHBOURING) {
maze[i][j].setDown(Constants.INNEIGHBOURING);
}
if (right[i][j] == Constants.NEIGHBOURING) {
maze[i][j].setRight(Constants.NEIGHBOURING);
}
if (right[i][j] == Constants.INNEIGHBOURING) {
maze[i][j].setRight(Constants.INNEIGHBOURING);
}
}
}
for (int i = Constants.GRID_SIZE - 1; i >= 0; i--) {
for (int j = Constants.GRID_SIZE - 1; j >= 0; j--) {
if (maze[i][j].getRight() == Constants.NEIGHBOURING) {
clearFence(i, j, i, j + 1, g);
}
if (maze[i][j].getDown() == Constants.NEIGHBOURING) {
clearFence(i, j, i + 1, j, g);
}
}
}
// 画左上角的入口
g.drawLine(padding, padding + 1, padding, padding + width - 1);
int last = padding + Constants.GRID_SIZE * width;
// 画右下角出口
g.drawLine(last, last - 1, last, last - width + 1);
// 画下边框
g.setColor(Color.BLACK);
g.drawLine(padding, last, last, last);
// 画右边框
g.drawLine(last, padding, last, last - width);
// 画路径
drawPath(g);
}
// 私有方法，目的是抹掉两个格子之间的边
private void clearFence(int i, int j, int fx, int fy, Graphics g) {
int sx = padding + ((j > fy ? j : fy) * width),
sy = padding + ((i > fx ? i : fx) * width),
dx = (i == fx ? sx : sx + width),
dy = (i == fx ? sy + width : sy);
if (sx != dx) {
sx++;
dx--;
} else {
sy++;
dy--;
}
g.drawLine(sx, sy, dx, dy);
}
// 由格子的行数列数，得到格子中心点的像素XY坐标
private int getCenterX(Cell p) {
return padding + p.getY() * width + width / 2;
}
private int getCenterY(Cell p) {
return padding + p.getX() * width + width / 2;
}
// 由序列数得到对应的行和列
private int getRow(int num) {
return (num ) / Constants.GRID_SIZE;
}
private int getCol(int num) {
return num % Constants.GRID_SIZE;
}
private void drawPath(Graphics g) {
g.setColor(Color.red);
// 已经得到初始路径到最后路径的list，接下来对照相应的格子，再画出来就行
for (int i = 0; i < path.size() - 1; i++) {
int first = path.get(i);
int second = path.get(i + 1);
g.drawLine(getCenterX(maze[getRow(first)][getCol(first)]), getCenterY(maze[getRow(first)][getCol(first)]), getCenterX(maze[getRow(second)][getCol(second)]), getCenterY(maze[getRow(second)][getCol(second)]));
}
}
public static void main(String[] args) {
JPanel test2 = new Test2();
JFrame frame = new JFrame("homework02.Maze");
//下面一行自动调用paintComponent方法
frame.setContentPane(test2);
frame.setSize(Constants.WIDTH + Constants.PADDING, Constants.WIDTH + Constants.PADDING + Constants.PADDING);
frame.setLocation(Constants.LX, Constants.LY);
frame.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);
frame.setVisible(true);
}
}