为什么我的DDPG算法结果堪忧？

Clever_Hans

已于 2025-03-24 17:19:24 修改

阅读量187

点赞数 4

CC 4.0 BY-SA版权

文章标签：人工智能 python 强化学习 DDPG 机械臂轨迹跟踪控制机械臂轨迹跟踪

于 2025-03-24 17:15:14 首次发布

本文链接：https://blog.youkuaiyun.com/wolves_fly/article/details/146480930

我想着是用DDPG算法+RISE控制器进行机械臂轨迹跟踪控制，由DDPG算法提供前馈力矩，在结合RISE的反馈力矩，然后根据逆动力学进行机械臂轨迹跟踪控制，但是DDPG算法一直不收敛或者效果不好，更改了很多次网络结构和奖励函数，设置的最大步长3000和最大回合数是1000，我的轨迹规划是用五次多项式做的，共30秒，每0.01秒控制一次，故一共3000个点，所以最大步长是3000，图片是训练过程中的图像，已经更换了很多次学习率和网络结构，效果依然不好。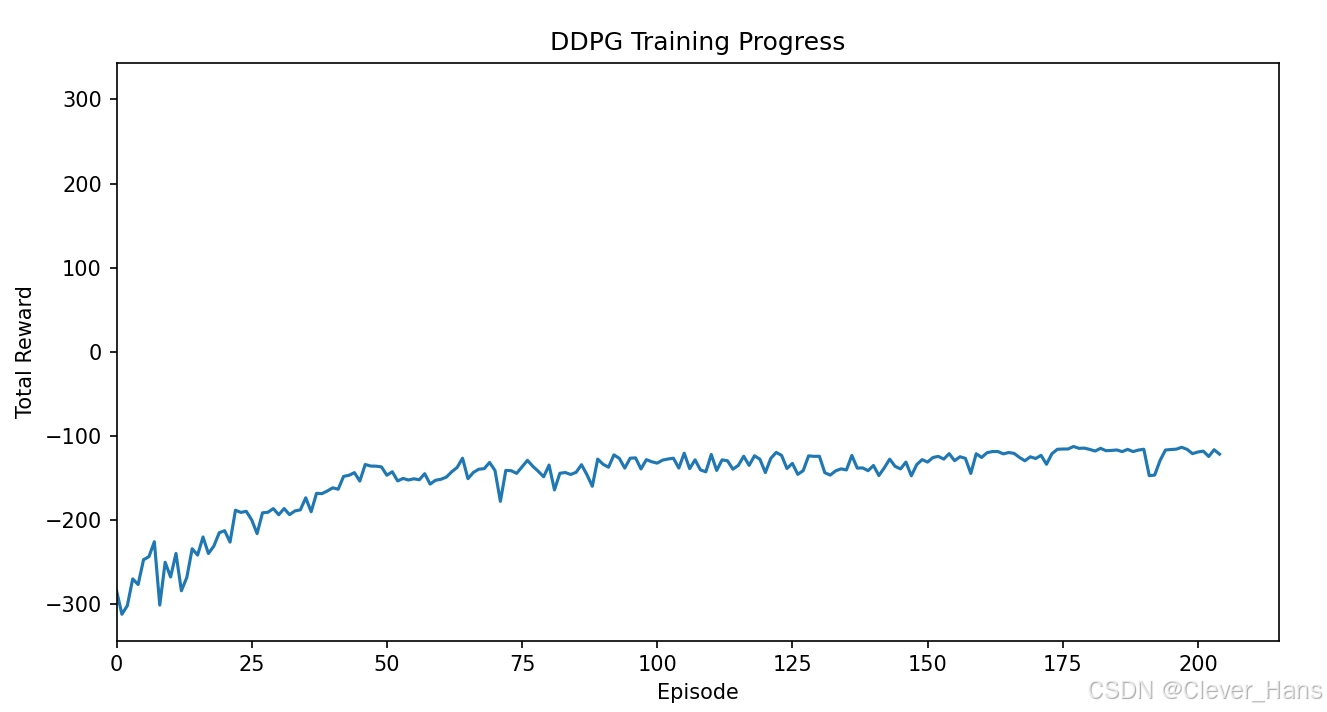

“RoboticArmEnv.py如下：”

import matplotlib.pyplot as plt
import numpy as np
import matlab.engine
# from onnx.reference.ops.aionnxml.op_svm_classifier import multiclass_probability


class RoboticArmEnv:
    def __init__(self, matlab_engine=None):
        self.matlab_engine = matlab_engine
        self.state_dim = 20
        self.action_dim = 5
        self.max_action = 60

        # 生成轨迹数据
        traj_data = self.generate_trajectory()
        self.trajectory_q = traj_data['qd']
        self.trajectory_dq = traj_data['dqd']
        self.trajectory_ddqd = traj_data['ddqd']
        self.total_steps = len(self.trajectory_q)

        # 初始化状态变量
        self.q = np.zeros(5)
        self.dq = np.zeros(5)
        self.target_q = self.trajectory_q[0]
        self.target_dq = self.trajectory_dq[0]
        self.target_ddqd = self.trajectory_ddqd[0]
        self.e = self.target_q - self.q
        self.de = self.target_dq - self.dq
        self.e_last = np.zeros(5)
        self.de_last = np.zeros(5)
        self.current_step = 0

    def generate_trajectory(self):
        """生成三次运动轨迹（总时间30秒）"""
        self.q0 = np.zeros(5)
        self.q_targets = [
            np.array([0.157, -0.178, 0.513, -0.431, -0.157]),
            np.array([0.5024, -0.637,0.806, -0.232, -0.9734]),
            np.array([0,0,0,0,0])
        ]

        t1 = np.linspace(0, 10, 1000)
        t2 = np.linspace(0, 10, 1000)
        t3 = np.linspace(0, 10, 1000)

        traj1 = self.quintic_interpolation(self.q0, self.q_targets[0], t1)
        traj2 = self.quintic_interpolation(self.q_targets[0], self.q_targets[1], t2)
        traj3 = self.quintic_interpolation(self.q_targets[1], self.q_targets[2], t3)

        full_traj = np.vstack([traj1, traj2, traj3])
        return {
            'qd': full_traj[:, :5],
            'dqd': full_traj[:, 5:10],
            'ddqd': full_traj[:, 10:]
        }

    def quintic_interpolation(self, q_start, q_end, t):
        tf = t[-1]
        t = t.reshape(-1, 1)

        a0 = q_start
        a1 = np.zeros_like(q_start)
        a2 = np.zeros_like(q_start)
        a3 = 10 * (q_end - q_start) / (tf ** 3)
        a4 = -15 * (q_end - q_start) / (tf ** 4)
        a5 = 6 * (q_end - q_start) / (tf ** 5)

        qd = a0 + a1 * t + a2 * t ** 2 + a3 * t ** 3 + a4 * t ** 4 + a5 * t ** 5
        dqd = a1 + 2 * a2 * t + 3 * a3 * t ** 2 + 4 * a4 * t ** 3 + 5 * a5 * t ** 4
        ddqd = 2 * a2 + 6 * a3 * t + 12 * a4 * t ** 2 + 20 * a5 * t ** 3

        return np.hstack([qd, dqd, ddqd])

    def update_RISE_new(self):
        """调用MATLAB的RISE控制器"""
        self.e = self.target_q - self.q
        self.de = self.target_dq - self.dq

        # 转换为MATLAB兼容格式
        e_matlab = matlab.double(self.e.tolist())
        de_matlab = matlab.double(self.de.tolist())
        # print(q_matlab)
        # 调用MATLAB函数
        mu = self.matlab_engine.update_RISE_new(e_matlab, de_matlab, nargout=1)
        return np.array(mu).flatten()

    def reset(self):
        """重置机械臂到初始状态"""
        self.current_step = 0
        # 初始化状态变量
        self.q = np.zeros(5)
        self.dq = np.zeros(5)
        self.target_q = self.trajectory_q[0]
        self.target_dq = self.trajectory_dq[0]
        self.target_ddqd = self.trajectory_ddqd[0]
        self.e = self.target_q - self.q
        self.de = self.target_dq - self.dq
        # self.e_last = np.zeros(5)
        # self.de_last = np.zeros(5)
        return self._get_state()

    def step(self, action, mu, d):
        """执行动作，返回新状态、奖励、是否终止,d是扰动"""
        # 执行动力学计算
        tau_total = action + mu
        print('action1',action)
        print('tt',tau_total)
        # next_state_mu = self._call_matlab_dynamics(mu,d)
        next_state_total = self._call_matlab_dynamics(tau_total,d)
        # next_state_tau = self._call_matlab_dynamics(action)

        # 更新目标到下一时间步
        self.current_step = min(self.current_step + 1, self.total_steps - 1)
        self.target_q = self.trajectory_q[self.current_step]
        self.target_dq= self.trajectory_dq[self.current_step]
        self.target_ddqd = self.trajectory_ddqd[self.current_step]

        # q_mu = next_state_mu[:5]
        # dq_mu = next_state_mu[5:10]
        q_total = next_state_total[:5]
        dq_total = next_state_total[5:10]
        # q_err_mu = q_mu - self.target_q
        # dq_err_mu = dq_mu - self.target_dq
        q_err_total = q_total - self.target_q
        dq_err_total = dq_total - self.target_dq
        # mu_err = np.linalg.norm(q_err_mu,ord=1)+np.linalg.norm(dq_err_mu,ord=1)
        # total_err = np.linalg.norm(q_err_total,ord=1)+np.linalg.norm(dq_err_total,ord=1)

        # q_tau = next_state_tau[:5]
        # dq_tau = next_state_tau[5:10]
        # q_err_tau = q_tau - self.target_q
        # dq_err_tau = dq_tau - self.target_dq


        # # 更新状态
        # if mu_err < total_err:
        #     self.q = next_state_mu[:5]
        #     self.dq = next_state_mu[5:10]
        #     next_state = next_state_mu
        # else:
        #     self.q = next_state_total[:5]
        #     self.dq = next_state_total[5:10]
        #     next_state = next_state_total
        # 更新状态
        # self.q = self.target_q
        # self.dq = self.target_dq
        # next_state = next_state_tau
        self.q = next_state_total[:5]
        self.dq = next_state_total[5:10]
        next_state = next_state_total

        # 计算奖励
        reward = self._calculate_reward(tau_total, q_err_total, dq_err_total)
        done = self._check_termination(q_err_total, dq_err_total)

        # reward = self._calculate_reward(action, q_err_tau, dq_err_tau)
        # done = self._check_termination(q_err_tau, dq_err_tau)

        return next_state, reward, done, {}

    def _get_state(self):
        """获取当前状态：关节角度+速度+目标信息"""
        return np.concatenate([
            self.q,
            self.dq,
            self.target_q,
            self.target_dq,
        ])

    def _call_matlab_dynamics(self, tau, d):
        """调用MATLAB计算动力学 ，tau带扰动"""
        # 将tau传递给MATLAB并获取下一状态
        self.matlab_engine.workspace['tau'] = tau.tolist()
        tau_matlab = matlab.double(tau.tolist())
        e = matlab.double(self.e.tolist())
        de = matlab.double(self.de.tolist())
        qd = matlab.double(self.target_q.tolist())
        dqd = matlab.double(self.target_dq.tolist())
        ddqd = matlab.double(self.target_ddqd.tolist())
        q_new, dq_new = self.matlab_engine.sim_step_new(tau_matlab,d, e,de,qd,dqd,ddqd, nargout=2)
        # 转换为NumPy数组并确保一维
        q_new = np.array(q_new).flatten()  # 转换为1×5，再展平为(5,)
        dq_new = np.array(dq_new).flatten()  # 转换为1×5，再展平为(5,)
        target_q = np.array(self.target_q).flatten()
        target_dq = np.array(self.target_dq).flatten()
        return np.concatenate([q_new, dq_new, target_q, target_dq])

    def _calculate_reward(self,action, q_total_err, dq_total_err):
        """奖励函数设计（关键！）"""
        q_err = q_total_err
        qd_err = dq_total_err
        # print(action)
        # print(q_err)
        # print(qd_err)
        # 奖励项设计
        # position_reward = -0.1 * np.sum(q_err ** 2)  # 角度误差惩罚
        # velocity_reward = -0.1 * np.sum(qd_err ** 2)  # 速度误差惩罚
        # control_penalty = -0.001 * np.sum(action ** 2)  # 控制量惩罚

        position_reward = -1*np.linalg.norm(q_err) # 位置误差奖励
        velocity_reward = -1*np.linalg.norm(qd_err)

        # e_reward = 5*np.all(np.abs(q_err)<0.1) - 2*np.all(np.abs(q_err)>=0.1) # 角度误差奖励
        # de_reward = 5 * np.all(np.abs(qd_err) < 0.1) - 2 * np.all(np.abs(qd_err) >= 0.1) # 角速度误差奖励

        # # 边界奖励
        # if np.abs(self.q[0])<=-np.pi/2 and -85*np.pi/180<=self.q[1]<=0 and -10*np.pi/180 <=self.q[2] <=95*np.pi/180 and np.abs(self.q[3])<=95*np.pi/180 and np.abs(self.q[4])<=np.pi/2:
        #     b_reward = 0
        # else :
        #     b_reward = -100

        # 边界惩罚（连续）
        boundary_violation = np.sum(np.clip(
            [abs(self.q[0]) - np.pi / 2,
             -85 * np.pi / 180 - self.q[1],
             self.q[1] - 0,
             -self.q[2] - 10 * np.pi / 180,
             self.q[2] - 95 * np.pi / 180,
             abs(self.q[3]) - 95 * np.pi / 180,
             abs(self.q[4]) - np.pi / 2
             ], 0, None))  # 计算超出边界的量
        b_reward = - 10 * boundary_violation  # 按超出程度惩罚
        print(b_reward)

        # 成功奖励（误差<0.1°时饱和奖励）
        success_threshold = 0.0017   # 0.1度
        if np.all(np.abs(q_err)< success_threshold) :
            success_bonus = 100
        elif np.all(np.abs(q_err) < 0.017):
            success_bonus = 5   # 再给一次奖励
        elif np.all(np.abs(q_err) < 0.17):
            success_bonus = 1   # 再给一次奖励
        else:
            success_bonus = 0
        # success_bonus = 100 * np.exp(-np.linalg.norm(q_err))  # 误差越小，奖励越大

        if np.all(np.abs(qd_err)< success_threshold) :
            success_bonus_dq = 100
        elif np.all(np.abs(qd_err)< 0.017) :
            success_bonus_dq = 5   # 再给一次奖励
        elif np.all(np.abs(qd_err) < 0.17):
            success_bonus_dq = 1   # 再给一次奖励
        else:
            success_bonus_dq = 0
        # success_bonus_dq = 100 * np.exp(-np.linalg.norm(qd_err))  # 误差越小，奖励越大
        print(success_bonus)
        print(success_bonus_dq)

        return success_bonus + success_bonus_dq + b_reward + position_reward + velocity_reward

    def _check_termination(self,q_total_err, dq_err_tau):
        """终止条件判断"""
        # # print(np.linalg.norm(state[:5] - self.target_q))
        # return np.linalg.norm(q_total_err*180/np.pi,ord=2) < 1 and np.linalg.norm(dq_err_tau*180/np.pi,ord=2) < 1   # 位置和速度误差<0.1°

        # if self.current_step < 100:
        #     threshold = 50  # 初期宽松
        # elif self.current_step < 500:
        #     threshold = 30  # 中期适中
        # elif self.current_step < 2000:
        #     threshold = 10  # 中期适中
        # elif self.current_step < 4000:
        #     threshold = 1  # 中期适中
        # else:
        threshold = 0.1  # 后期严格
        return (
                np.linalg.norm(q_total_err * 180 / np.pi, ord=2) < threshold
                and np.linalg.norm(dq_err_tau * 180 / np.pi, ord=2) < threshold
        )

    def _plot(self):
        plt.plot(self.target_q)
        plt.plot(self.target_dq)


“DDPG.py如下：”
import numpy as np  # 导入 NumPy，用于处理数组和数学运算
import torch  # 导入 PyTorch，用于构建和训练神经网络
import torch.nn as nn  # 导入 PyTorch 的神经网络模块
import torch.optim as optim  # 导入 PyTorch 的优化器模块
from collections import deque  # 导入双端队列，用于实现经验回放池
import random  # 导入随机模块，用于从经验池中采样



# 定义 Actor 网络（策略网络）
class Actor(nn.Module):
    def __init__(self, state_dim = 20, action_dim = 5, max_action = 60.0):
        super(Actor, self).__init__()
        self.layer1 = nn.Linear(state_dim, 300)
        # self.bn1 = nn.BatchNorm1d(256)  # 批量归一化
        self.layer2 = nn.Linear(300, 128)
        # self.layer3 = nn.Linear(128, 64)
        # # self.layer_norm2 = nn.LayerNorm(64)
        # self.layer3 = nn.Linear(128, 64)
        # self.layer4 = nn.Linear(64, 32)
        self.layer3 = nn.Linear(128, action_dim)  # 隐藏层4到输出层，输出动作维度
        self.max_action = max_action  # 动作的最大值，用于限制输出范围

    def forward(self, state):
        x = torch.relu(self.layer1(state))  # 使用 ReLU 激活函数处理隐藏层1
        # x = torch.relu(self.layer1(state))  # 使用 ReLU 激活函数处理隐藏层1
        x = torch.relu(self.layer2(x))  # 使用 ReLU 激活函数处理隐藏层2
        # x = torch.relu(self.layer3(x)) # 使用 ReLU 激活函数处理隐藏层3
        # x = torch.relu(self.layer4(x))  # 使用 ReLU 激活函数处理隐藏层4
        x = torch.tanh(self.layer3(x)) * self.max_action# 使用 tanh 激活函数，并放大到动作范围
        # x = torch.tanh(self.layer4(x))
        # x = torch.tanh(self.layer3(x))
        return x  # 返回输出动作

# 定义 Critic 网络（价值网络）
class Critic(nn.Module):
    def __init__(self, state_dim = 20, action_dim = 5):
        super(Critic, self).__init__()
        self.layer1 = nn.Linear(state_dim + action_dim, 400)  # 将状态和动作拼接后输入到隐藏层1
        # self.bn1 = nn.BatchNorm1d(256)  # 批量归一化
        self.layer2 = nn.Linear(400, 300)
        # # self.layer_norm2 = nn.LayerNorm(64)
        self.layer3 = nn.Linear(300, 100)
        # self.layer4 = nn.Linear(64, 32)
        self.layer4 = nn.Linear(100, 1)  # 隐藏层4到输出层，输出动作维度

    def forward(self, state, action):
        x = torch.cat([state, action], dim = 1)  # 将状态和动作拼接为单个输入
        x = torch.relu(self.layer1(x))  # 使用 ReLU 激活函数处理隐藏层1
        # x = torch.relu(self.layer1(x))  # 使用 ReLU 激活函数处理隐藏层1
        x = torch.relu(self.layer2(x))  # 使用 ReLU 激活函数处理隐藏层2
        x = torch.relu(self.layer3(x))  # 使用 ReLU 激活函数处理隐藏层3
        # x = torch.relu(self.layer4(x))  # 使用 ReLU 激活函数处理隐藏层4
        x = self.layer4(x) # 输出 Q 值
        # print(x)
        return x  # 返回 Q 值


# 定义经验回放池
class ReplayBuffer:
    def __init__(self, max_size):
        self.buffer = deque(maxlen=max_size)  # 初始化一个双端队列，设置最大容量

    def add(self, state, action, reward, next_state, done):
        self.buffer.append((state, action, reward, next_state, done))  # 将经验存入队列

    def sample(self, batch_size):
        batch = random.sample(self.buffer, batch_size)  # 随机采样一个小批量数据
        states, actions, rewards, next_states, dones = zip(*batch)  # 解压采样数据
        return (np.array(states), np.array(actions), np.array(rewards),
                np.array(next_states), np.array(dones))  # 返回 NumPy 数组格式的数据

    def size(self):
        return len(self.buffer)  # 返回经验池中当前存储的样本数量

# DDPG智能体类定义
class DDPGAgent:
    # 初始化方法，设置智能体的参数和模型
    def __init__(self, state_dim = 20, action_dim=5, max_action=60, gamma=0.98, tau=0.01, buffer_size=1000000, batch_size=64):
        # 定义actor网络（策略网络）及其目标网络
        self.actor = Actor(state_dim, action_dim, max_action)
        self.actor_target = Actor(state_dim , action_dim, max_action)
        # 将目标actor网络的参数初始化为与actor网络一致
        self.actor_target.load_state_dict(self.actor.state_dict())
        # 定义actor网络的优化器
        self.actor_optimizer = optim.Adam(self.actor.parameters(), lr=1e-3)

        # 定义critic网络（值网络）及其目标网络
        self.critic = Critic(state_dim, action_dim)
        self.critic_target = Critic(state_dim, action_dim)
        # 将目标critic网络的参数初始化为与critic网络一致
        self.critic_target.load_state_dict(self.critic.state_dict())
        # 定义critic网络的优化器
        self.critic_optimizer = optim.Adam(self.critic.parameters(), lr=5e-3)

        # 保存动作的最大值，用于限制动作范围
        self.max_action = max_action
        # 折扣因子，用于奖励的时间折扣
        self.gamma = gamma
        # 软更新系数，用于目标网络的更新
        self.tau = tau
        # 初始化经验回放池
        self.replay_buffer = ReplayBuffer(buffer_size)
        # 每次训练的批量大小
        self.batch_size = batch_size

    # 选择动作的方法
    def select_action(self, state):
        # 将状态转换为张量
        state = torch.FloatTensor(state.reshape(1, -1))
        # 使用actor网络预测动作，并将结果转换为NumPy数组
        action = self.actor(state).detach().numpy().flatten()
        # print(action)
        return action

    # 训练方法
    def train(self):
        # 如果回放池中样本数量不足，直接返回
        if self.replay_buffer.size() < self.batch_size:
            return

        # 从回放池中采样一批数据
        states, actions, rewards, next_states, dones = self.replay_buffer.sample(self.batch_size)

        # 将采样的数据转换为张量
        states = torch.FloatTensor(states)
        # print(states[0][:5])
        # print(torch.FloatTensor(states.tolist())[0][:5])
        actions = torch.FloatTensor(actions)
        # print(actions.shape)
        rewards = torch.FloatTensor(rewards).unsqueeze(1)  # 添加一个维度以匹配Q值维度
        next_states = torch.FloatTensor(next_states)
        dones = torch.FloatTensor(dones).unsqueeze(1)  # 添加一个维度以匹配Q值维度


        # 计算target Q值
        with torch.no_grad():
            next_actions = self.actor_target(next_states)
            target_q = self.critic_target(next_states, next_actions)
            target_q = rewards + (1 - dones) * self.gamma * target_q
            # print('12345:',target_q)

        # 计算当前Q值
        current_q = self.critic(states, actions)
        # print("now_Q:",current_q.shape)
        # print(current_q.shape)

        # Critic损失
        critic_loss = nn.MSELoss()(current_q, target_q)
        self.critic_optimizer.zero_grad()
        critic_loss.backward()
        self.critic_optimizer.step()

        # Actor损失（最大化Q值）
        actor_actions = self.actor(states)
        actor_loss = -self.critic(states, actor_actions).mean()
        self.actor_optimizer.zero_grad()
        actor_loss.backward()
        self.actor_optimizer.step()

        # 更新目标网络参数（软更新）
        for target_param, param in zip(self.critic_target.parameters(), self.critic.parameters()):
            target_param.data.copy_(self.tau * param.data + (1 - self.tau) * target_param.data)

        for target_param, param in zip(self.actor_target.parameters(), self.actor.parameters()):
            target_param.data.copy_(self.tau * param.data + (1 - self.tau) * target_param.data)

    # 将样本添加到回放池中
    def add_to_replay_buffer(self, state, action, reward, next_state, done):
        self.replay_buffer.add(state, action, reward, next_state, done)


“train_ddpg.py如下：”

import math
import os
# 允许重复加载OpenMP库的临时解决方案（放在所有import之前）
os.environ['KMP_DUPLICATE_LIB_OK'] = 'True'
import numpy as np
import torch
import matplotlib.pyplot as plt  # 注意：在torch之后导入matplotlib
from DDPG import DDPGAgent
from RoboticArmEnv import RoboticArmEnv
import matlab.engine

# ================== 初始化部分 ================== #
# 启动MATLAB引擎
eng = matlab.engine.start_matlab()
eng.cd(r'D:\AAAA_HY\HY-M\deepseek\Really')  # 指向包含sim_step.m的目录

# 创建环境时传入引擎
env = RoboticArmEnv(matlab_engine=eng)
agent = DDPGAgent(state_dim=env.state_dim, action_dim=env.action_dim, max_action=env.max_action)
# ================== 新增OU噪声类 ================== #
class OUNoise:
    def __init__(self, action_dim, mu=0.0, theta=0.15, sigma=0.3, dt=0.01):
        """
        OU噪声生成器
        :param action_dim: 动作维度
        :param mu: 均值 (默认0)
        :param theta: 回归速率参数 (越大回归越快)
        :param sigma: 波动率参数 (噪声强度)
        :param dt: 时间步长 (需与环境步长一致)
        """
        self.action_dim = action_dim
        self.mu = mu
        self.theta = theta
        self.sigma = sigma
        self.dt = dt
        self.reset()

    def reset(self):
        """重置噪声过程"""
        self.state = np.ones(self.action_dim) * self.mu

    def sample(self):
        """生成噪声样本"""
        dx = self.theta * (self.mu - self.state) * self.dt
        dx += self.sigma * np.sqrt(self.dt) * np.random.normal(size=self.action_dim)
        self.state += dx
        return self.state

# ================== 修改训练循环 ================== #
# 初始化OU噪声（在训练循环外部）
ou_noise = OUNoise(
    action_dim=env.action_dim,
    theta=0.15,    # 回归速率（默认0.15）
    sigma=0.5,     # 初始噪声强度（默认0.3）
    dt=0.01 )       # 需与环境步长一致
max_episodes = 1000
max_steps = 1000
reward_history = []  # 用于存储每回合的总奖励

# ================== 可视化初始化 ================== #
plt.ion()  # 启用交互模式
fig, ax = plt.subplots(figsize=(10, 5))
ax.set_title("DDPG Training Progress")
ax.set_xlabel("Episode")
ax.set_ylabel("Total Reward")
line, = ax.plot([], [])  # 创建空线图

# ================== 训练循环 ================== #

for ep in range(max_episodes):
    num = 0
    state = env.reset()

    total_reward = 0

    ou_noise.reset()  # 每回合重置噪声

    # 噪声衰减参数
    noise_decay = 0.995
    current_noise_scale = 1  # 初始噪声幅度

    for step in range(max_steps):
        action = agent.select_action(state)
        # print("action:",action)
        # 生成OU噪声并缩放
        noise = ou_noise.sample()
        scaled_noise = current_noise_scale * noise
        d = np.ones(5)@np.diag([math.sin(step),math.cos(step),math.sin(step),math.cos(step),math.sin(step)])
        # action = action - np.ones(5)@np.diag([math.sin(step),math.cos(step),math.sin(step),math.cos(step),math.sin(step)])
        # noise = noise * decay
        # 应用噪声并限幅
        action = action + scaled_noise
        action = np.clip(action, -agent.max_action, agent.max_action)

        # 获取RISE控制量
        mu = env.update_RISE_new()  # 自动使用当前状态计算

        next_state, reward, done, _ = env.step(action, mu, d)
        # action_total = action + mu
        # print(next_state)
        # print(next_state.size)
        agent.add_to_replay_buffer(state, action, reward, next_state, done)
        # if step % 5 == 0:
        agent.train()

        total_reward += reward
        state = next_state
        current_noise_scale *= noise_decay
        num += 1

        if done:
            break

    # ================== 更新可视化 ================== #
    if (ep + 1) % 50 == 0:  # 每50轮保存一次
        torch.save(agent.actor.state_dict(),f"continue_{ep + 1:04d}_actor.pth")
        torch.save(agent.actor_target.state_dict(),f"continue_{ep + 1:04d}_actor_target.pth")
        np.save(f"continue_{ep + 1:04d}_rewards.npy", reward_history)
        torch.save( agent.critic.state_dict(), f"continue_{ep + 1:04d}_critic.pth")
        torch.save(agent.critic_target.state_dict(),f"continue_{ep + 1:04d}_critic_target.pth")
        # np.save(f"continue_{ep + 1:04d}_rewards.npy", reward_history)
    # torch.save(agent.actor.state_dict(), f"Episode: {ep + 1:4d}_Total Reward: {total_reward:7.2f}.pth")
    total_reward = total_reward / num             #  平均奖励
    reward_history.append(total_reward)
    # print(total_reward)
    # 更新线图数据
    line.set_xdata(np.arange(len(reward_history)))
    line.set_ydata(reward_history)

    # 动态调整坐标轴范围
    ax.set_xlim(0, len(reward_history) + 10)
    y_min = min(reward_history) * 1.1 if min(reward_history) < 0 else 0
    y_max = (min(reward_history)) * -1.1
    ax.set_ylim(y_min, y_max)

    # 重绘图形
    fig.canvas.draw()
    fig.canvas.flush_events()

    # ================== 打印训练进度 ================== #
    print(f"Episode: {ep + 1:4d} | "
          f"Total Reward: {total_reward:7.2f} | "
          f"Average Reward: {np.mean(reward_history[-10:]):7.2f} | "
          f"Max Reward: {max(reward_history):7.2f}")
# ================== 训练后处理 ================== #
# 保存训练好的Actor网络
# torch.save(agent.actor.state_dict(), "best_ddpg_actor_arm_plot+zao_update_continue.pth")
# # 保存奖励历史数据
# np.save("best_ddpg_actor_arm_plot+zao_update_continue.npy", reward_history)



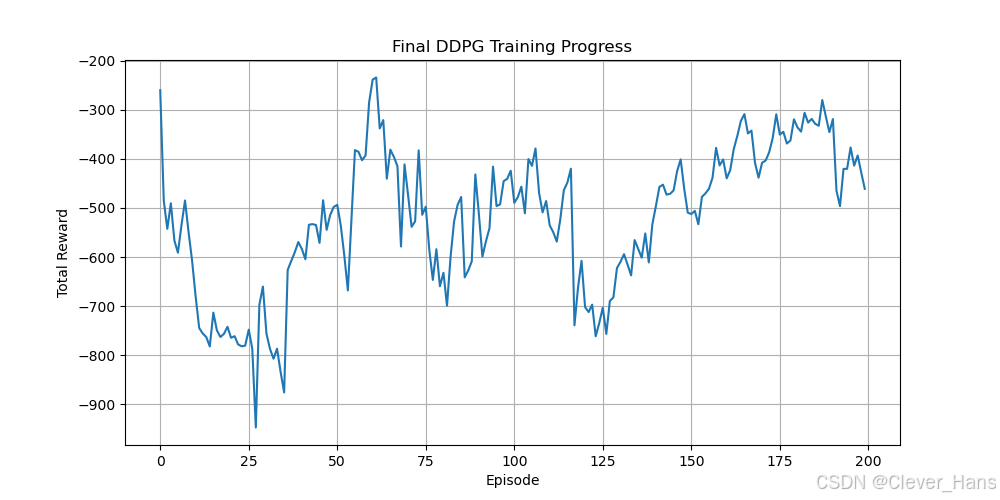
# 最终绘制完整曲线
plt.ioff()  # 关闭交互模式
plt.figure(figsize=(10, 5))
plt.plot(reward_history)
plt.title("Final DDPG Training Progress")
plt.xlabel("Episode")
plt.ylabel("Total Reward")
plt.grid(True)
plt.savefig("best_ddpg_actor_arm_plot+zao_update_continue.png")
plt.show()

# 关闭MATLAB引擎
eng.quit()

env._plot()

我调用的matlab代码如下，主要用于实现机械臂动力学求解：

“update_RISE_new.m如下”

function mu = update_RISE_new(e, de)    % q dq 为行向量 e de 为列向量 ddqd,dqd为行向量

    persistent integral_term Lambda kh dt robot k2 ks alpha1
 % 初始化持久变量  
    if isempty(robot)
        integral_term = zeros(5,1);            % 积分项初始化
        Lambda = diag([8, 8, 8, 8, 8]);        % 滑模面增益-
        alpha1 = diag([0.2, 0.2, 0.2, 0.2, 0.2]);
        ks = diag([0.50 0.50 0.50 0.50 0.50]);
        k2 = diag([2 2 2 2 2]);
        kh=diag([100 100 100 100 100]);
        dt = 0.01;

        % 机械臂建模（Modified DH参数）
        L(1) = Link('revolute', 'd', 0, 'a', 0, 'alpha', 0, 'modified', ...
            'm', 3.0, 'r', [0 0 0], 'I', diag([0.0025, 0.0025, 0.0025]), 'qlim', [-pi/2, pi/2]);
        L(2) = Link('revolute', 'd', 0, 'a', 0, 'alpha', -pi/2, 'modified', ...
            'm', 2.8, 'r', [0 0 0], 'I', diag([0.0037, 0.0037, 0.0023]), 'qlim', [-85*pi/180, 0]);
        L(3) = Link('revolute', 'd', 0, 'a', 0.3, 'alpha', 0, 'modified', ...
            'm', 2.8, 'r', [0.15 0 0], 'I', diag([0.0035, 0.0852, 0.0887]), 'qlim', [-10*pi/180, 95*pi/180]);
        L(4) = Link('revolute', 'd', 0, 'a', 0.5, 'alpha', 0, 'modified', ...
            'm', 2.8, 'r', [0.25 0 0], 'I', diag([0.0035, 0.2317, 0.2352]), 'qlim', [-95*pi/180, 95*pi/180]);
        L(5) = Link('revolute', 'd', 0.3, 'a', 0, 'alpha', -pi/2, 'modified', ...
            'm', 1.0, 'r', [0 0 0.15], 'I', diag([0.090, 0.090, 0.06]), 'qlim', [-pi/2, pi/2]);
        
        robot = SerialLink(L, 'name', 'Dobot MG400');
        robot.gravity = [0 0 -9.81];  % 重力方向
    end
    % 计算滑模面
    if isrow(e)
        e = e';
    end
    if isrow(de)
        de = de';
    end
    z2 = de + Lambda*e;
    
    % 符号函数平滑处理
    smoothed_sign = tanh(kh*z2);
    
    % 更新积分项（梯形积分法）
    integral_term = integral_term + alpha1*smoothed_sign*dt + (ks+diag([1,1,1,1,1]))*k2*z2*dt;
   
    mu = (ks+diag([1,1,1,1,1]))*z2  + integral_term; %5*1
    % % RISE控制律
    % % tau = M *(ddqd' + Lambda*de) + dC*dqd' + dG + dF + mu;
    % tau = M *(ddqd') + C*dqd' + G + F + mu;
    % % disp(mu)
end










“sim_step_new.m如下：”
%% 动力学计算函数
function [q_new, dq_new] = sim_step_new(tau,d, e, de, qd,dqd, ddqd) % d为扰动项，5*1
    % e,de:5*1; qd,dqd,ddqd:1*5 ,tau=fd_hat+mu-d
    persistent robot q dq dt Lambda k2 k1 fk fv
    
    % 首次调用时初始化所有 persistent 变量
    if isempty(robot)
        disp('Initializing robot, q, qd, dt'); % 调试输出
        
        % 初始化机械臂模型
        L(1) = Link('revolute', 'd', 0, 'a', 0, 'alpha', 0, 'modified', ...
            'm', 3.0, 'r', [0 0 0], 'I', diag([0.0025, 0.0025, 0.0025]), 'qlim', [-pi/2, pi/2]);
        L(2) = Link('revolute', 'd', 0, 'a', 0, 'alpha', -pi/2, 'modified', ...
            'm', 2.8, 'r', [0 0 0], 'I', diag([0.0037, 0.0037, 0.0023]), 'qlim', [-85*pi/180, 0]);
        L(3) = Link('revolute', 'd', 0, 'a', 0.3, 'alpha', 0, 'modified', ...
            'm', 2.8, 'r', [0.15 0 0], 'I', diag([0.0035 , 0.0852, 0.0887]), 'qlim', [-10*pi/180, 95*pi/180]);
        L(4) = Link('revolute', 'd', 0, 'a', 0.5, 'alpha', 0, 'modified', ...
            'm', 2.8, 'r', [0.25 0 0], 'I', diag([0.0035, 0.2317, 0.2352]), 'qlim', [-95*pi/180, 95*pi/180]);
        L(5) = Link('revolute', 'd', 0.3, 'a', 0, 'alpha', -pi/2, 'modified', ...
            'm', 1.0, 'r', [0 0 0.15], 'I', diag([0.090, 0.090, 0.06]), 'qlim', [-pi/2, pi/2]);
        
        robot = SerialLink(L, 'name', 'Dobot MG400');
        robot.gravity = [0 0 -9.81];  % 重力方向
        
        % 初始化状态变量
        q = [0, 0, 0, 0, 0];    % 初始关节角度
        dq = [0, 0, 0, 0, 0];   % 初始关节速度
        dt = 0.01;           % 积分步长
        Lambda = diag([0.1, 0.1, 0.1, 0.1, 0.1]);        % 滑模面增益-
        k2 = diag([2 2 2 2 2]);
        k1 = Lambda;
        fk = [0.2 0.2 0.2 0.2 0.2];
        fv = [0.1 0.1 0.1 0.1 0.1];
    end

    % 确保tau为行向量
    if iscolumn(tau)
        tau = tau';
    end
    if isrow(d)
        d = d';
    end
    if isrow(e)
        e = e';
    end
    if isrow(de)
        de = de';
    end
    if iscolumn(qd)
        qd = qd';
    end
    if iscolumn(dqd)
        dqd = dqd';
    end
    if iscolumn(ddqd)
        ddqd = ddqd';
    end
    try
        z2 = de + Lambda*e;
        % 计算动力学项
        M = robot.inertia(q)';         % 惯性矩阵
        C = robot.coriolis(q, dq)';% 科氏力矩阵
        G = robot.gravload(q)';        % 重力项
        F = robot.friction(dq)';  % 获取摩擦力

        dM = robot.inertia(qd)';         % 惯性矩阵
        dC = robot.coriolis(qd, dqd)';% 科氏力矩阵
        dG = robot.gravload(qd)';        % 重力项
        dF = friction(fk,fv,dqd)';  % 获取摩擦力
    
        fd = dM*ddqd'+dC*dqd'+dF+dG;  % 5*1
        S = M*(k1*de+k2*z2) + M*ddqd'-dM*ddqd' + C*dq'-dC*dqd'+F-dF+G-dG; % 5*1
        % 机械臂动力学仿真（前向欧拉法）
        ddq = ddqd' + (k1+k2)*de+k1*k2*e-M\(fd+S+d-tau');  % d为扰动项，5*1
        % disp(k)
        dq = dq + ddq'*dt;
        q = q + dq*dt + 0.5*ddq'*dt^2;

        q_new = q;
        dq_new = dq;
        % print(q)
        
    catch ME
        disp(['error: ' ME.message]);
        q_new = q;
        dq_new = dq;
    end
    
end