Hierarchical task network&STRIPS

理解Hierarchical Task Network与STRIPS在人工智能规划中的应用

最新推荐文章于 2025-08-18 15:10:35 发布

wolf96

最新推荐文章于 2025-08-18 15:10:35 发布

阅读量1.7k

点赞数

分类专栏： AI

AI 专栏收录该内容

16 篇文章

订阅专栏

本文深入探讨了Hierarchical Task Network（HTN）和STRIPS在人工智能规划领域的核心概念和应用，包括它们如何通过任务网络表达依赖关系，以及在解决复杂任务时提供的优势。同时，文章还介绍了这两种方法在实际规划问题中的实例，并讨论了其复杂性和已有的实现工具。

Hierarchical task network

原文：https://en.wikipedia.org/wiki/Hierarchical_task_network

In artificial intelligence, the hierarchical task network, or HTN, is an approach to automated planning in which the dependency among actions can be given in the form of networks.

Planning problems are specified in the hierarchical task network approach by providing a set of tasks, which can be:

primitive tasks, which roughly correspond to the actions of STRIPS;
compound tasks, which can be seen as composed of a set of simpler tasks;
goal tasks, which roughly corresponds to the goals of STRIPS, but are more general.

A primitive task is an action that can be executed. A compound task is a complex task composed of a sequence of actions. A goal task is a task of satisfying a condition. The difference between primitive and other tasks is that the primitive actions can be directly executed. Compound and goal tasks both require a sequence of primitive actions to be performed; however, goal tasks are specified in terms of conditions that have to be made true, while compound tasks can only be specified in terms of other tasks via the task network outlined below.

Constraints among tasks are expressed in form of networks, called task networks. A task network is a set of tasks and constraints among them. Such a network can be used as the precondition for another compound or goal task to be feasible. This way, one can express that a given task is feasible only if a set of other actions (those mentioned in the network) are done, and they are done in such a way that the constraints among them (specified by the network) are satisfied. One particular formalism for representing hierarchical task networks that has been fairly widely used is TAEMS.

A task network can for example specify that a condition is necessary for a primitive action to be executed. When this network is used as the precondition for a compound or goal task, it means that the compound or goal task requires the primitive action to be executed and that the condition must be true for its execution to successfully achieve the compound or goal task.

The best-known domain-independent HTN-planning software is:

Nonlin, one of the first HTN planning systems.^[1]
SIPE-2^[2]
O-Plan^[3]
UMCP, the first provably sound and complete HTN planning systems.^[4]
SHOP2, a HTN-planner developed at University of Maryland, College Park.^[5]
HTNPlan-P, preference-based HTN planning.^[6]

STRIPS

原文：https://en.wikipedia.org/wiki/STRIPS

In artificial intelligence, STRIPS (Stanford Research Institute Problem Solver) is anautomated planner developed by Richard Fikes and Nils Nilsson in 1971 at SRI International.^[1] The same name was later used to refer to theformal language of the inputs to this planner. This language is the base for most of the languages for expressingautomated planning problem instances in use today; such languages are commonly known asaction languages. This article only describes the language, not the planner.

Definition

A STRIPS instance is composed of:

An initial state;
The specification of the goal states – situations which the planner is trying to reach;
A set of actions. For each action, the following are included:
- preconditions (what must be established before the action is performed);
- postconditions (what is established after the action is performed).

Mathematically, a STRIPS instance is a quadruple $\langle P,O,I,G \rangle$ , in which each component has the following meaning:

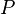$P$ is a set ofconditions (i.e., propositional variables);
$O$ is a set ofoperators (i.e., actions); each operator is itself a quadruple $\langle \alpha, \beta, \gamma, \delta \rangle$ , each element being a set of conditions. These four sets specify, in order, which conditions must be true for the action to be executable, which ones must be false, which ones are made true by the action and which ones are made false;
$I$ is the initial state, given as the set of conditions that are initially true (all others are assumed false);
$G$ is the specification of the goal state; this is given as a pair $\langle N,M \rangle$ , which specify which conditions are true and false, respectively, in order for a state to be considered a goal state.

A plan for such a planning instance is a sequence of operators that can be executed from the initial state and that leads to a goal state.

Formally, a state is a set of conditions: a state is represented by the set of conditions that are true in it. Transitions between states are modeled by a transition function, which is a function mapping states into new states that result from the execution of actions. Since states are represented by sets of conditions, the transition function relative to the STRIPS instance $\langle P,O,I,G \rangle$ is a function

\operatorname{succ}: 2^P \times O \rightarrow 2^P,

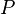where $2^P$ is the set of all subsets of $P$ , and is therefore the set of all possible states.

The transition function $\operatorname{succ}$ for a state $C \subseteq P$ , can be defined as follows, using the simplifying assumption that actions can always be executed but have no effect if their preconditions are not met:

$\operatorname{succ}(C,\langle \alpha,\beta,\gamma,\delta \rangle)$	= $C \backslash \delta \cup \gamma$	if $\alpha \subseteq C$ and $\beta \cap C = \varnothing$
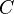	= $C$	otherwise

The function $\operatorname{succ}$ can be extended to sequences of actions by the following recursive equations:

\operatorname{succ}(C,[\ ]) = C

\operatorname{succ}(C,[a_1,a_2,\ldots,a_n])=\operatorname{succ}(\operatorname{succ}(C,a_1),[a_2,\ldots,a_n])

A plan for a STRIPS instance is a sequence of actions such that the state that results from executing the actions in order from the initial state satisfies the goal conditions. Formally, $[a_1,a_2,\ldots,a_n]$ is a plan for $G = \langle N,M \rangle$ if $F=\operatorname{succ}(I,[a_1,a_2,\ldots,a_n])$ satisfies the following two conditions:

N \subseteq F

M \cap F = \varnothing

Extensions

The above language is actually the propositional version of STRIPS; in practice, conditions are often about objects: for example, that the position of a robot can be modeled by apredicate $At$ , and $At(room1)$ means that the robot is in Room1. In this case, actions can havefree variables, which are implicitly existentially quantified. In other words, an action represents all possible propositional actions that can be obtained by replacing each free variable with a value.

The initial state is considered fully known in the language described above: conditions that are not in $I$ are all assumed false. This is often a limiting assumption, as there are natural examples of planning problems in which the initial state is not fully known. Extensions of STRIPS have been developed to deal with partially known initial states.

A sample STRIPS problem

A monkey is at location A in a lab. There is a box in location C. The monkey wants the bananas that are hanging from the ceiling in location B, but it needs to move the box and climb onto it in order to reach them.

Initial state: At(A), Level(low), BoxAt(C), BananasAt(B)
Goal state:    Have(Bananas)

Actions:
               // move from X to Y
               _Move(X, Y)_
               Preconditions:  At(X), Level(low)
               Postconditions: not At(X), At(Y)
               
               // climb up on the box
               _ClimbUp(Location)_
               Preconditions:  At(Location), BoxAt(Location), Level(low)
               Postconditions: Level(high), not Level(low)
               
               // climb down from the box
               _ClimbDown(Location)_
               Preconditions:  At(Location), BoxAt(Location), Level(high)
               Postconditions: Level(low), not Level(high)
               
               // move monkey and box from X to Y
               _MoveBox(X, Y)_
               Preconditions:  At(X), BoxAt(X), Level(low)
               Postconditions: BoxAt(Y), not BoxAt(X), At(Y), not At(X)
               
               // take the bananas
               _TakeBananas(Location)_
               Preconditions:  At(Location), BananasAt(Location), Level(high)
               Postconditions: Have(bananas)

Complexity

Deciding whether any plan exists for a propositional STRIPS instance is PSPACE-complete. Various restrictions can be enforced in order to decide if a plan exists in polynomial time or at least make it anNP-complete problem.^[2]