算法打卡day02|Leetcode977、209、58|复习之前数组双指针|滑动窗口思想、模拟行为——螺旋矩阵

本文链接：https://blog.youkuaiyun.com/wobujidao/article/details/135863859

Leetcode.977 有序数组的平方（数组双指针）

题目链接：https://leetcode.cn/problems/squares-of-a-sorted-array/description/

Java暴力解法：

class Solution {
    public int[] sortedSquares(int[] nums) {
        for(int i =0;i<nums.length;i++){
            nums[i] = (nums[i]*nums[i]);
        }
        Arrays.sort(nums);
        return nums;
    }
}
//先平方 再排序  当然用快排更好

根据力扣的进阶需求：

分析题目：

数组特性：两端大中间小，且有序，适合从两段选较大数向中间移动

解题思路：

使用双指针（i,j），分别指向数组左右两端，判断取数值平方的最大值
申请result 数组空间大小=数组nums，用于存储上面判断的结果
因为max一定位于数组两端，所以从两端开始遍历，将第比较结果存于新数组最末端
直到所有元素全部遍历存入，i>j结束

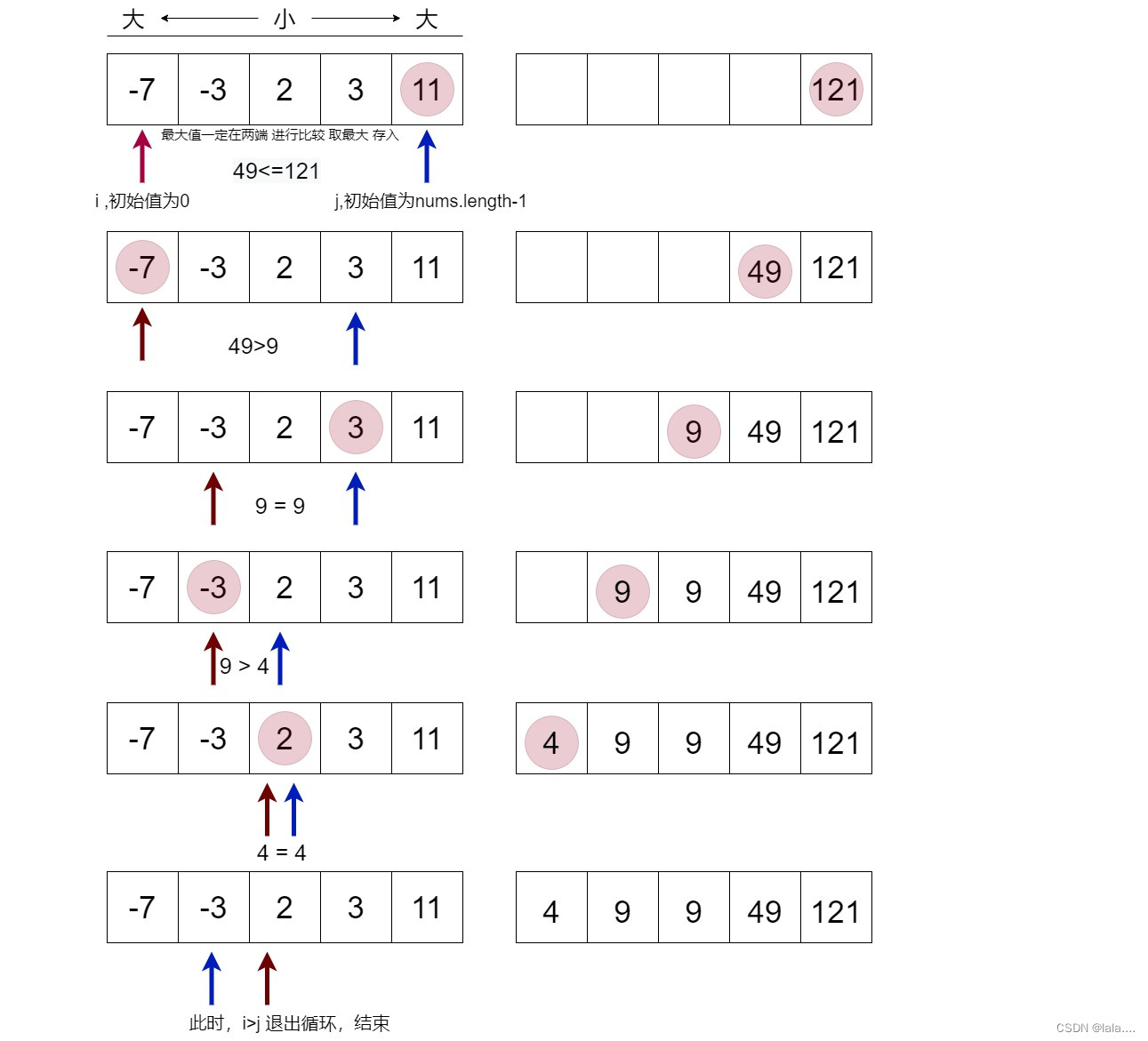
Java双指针实现代码：

class Solution {
    public int[] sortedSquares(int[] nums) {
        int L = nums.length;
        int[] resultnums = new int[L];
        int k = L-1;
        for(int i = 0 ,j = k;i<=j; ){
            if((nums[i]*nums[i])<=(nums[j]*nums[j])){
                resultnums[k] = nums[j]*nums[j];
                j--;
                k--;
            }else{
                resultnums[k] = nums[i]*nums[i];
                i++;
                k--; 
            }
        }
        return resultnums;
    }
}
//tips:i<=j  使用<= 而不是< 的原因：
//如果使用< 在ji指向同一元素时，程序直接退出了，会有一个元素没有遍历比较到，最后result数组就会缺少一个元素

总结：双指针如何取值及使用主要还是观察需要观察nums的特性

Leetcode.209 有序数组的平方

题目链接:https://leetcode.cn/problems/squares-of-a-sorted-array/description/

Java暴力拆解法：

里面的用例会通过，但是提交会超时

思路是双层for循环遍历分别表示数组起始与终止索引；

class Solution {
    public int minSubArrayLen(int target, int[] nums) {
        int resultL = nums.length+1;
        for(int begain = 0;begain<nums.length;begain++){
            int sum = 0;
            for(int end = begain;end<nums.length;end++){
                sum +=nums[end]; 
                int theL = end-begain+1;
                if(sum>=target){
                    resultL = Math.min(resultL,theL);
                    break;
                }
            }
        }
        return resultL<=nums.length?resultL:0;
    }
}

Java解法：滑动窗口思想

class Solution {
    public int minSubArrayLen(int target, int[] nums) {
        int resultL = nums.length+1;
        int sum = 0;
        for(int j = 0 , i = 0 ;j<nums.length;j++){
            sum +=nums[j];
            while(sum >= target){
                resultL = Math.min(resultL,j-i+1);
                sum = sum-nums[i++];
            }
        }
        return resultL<=nums.length?resultL:0;
    }
}

代码思路及总结：滑动窗口可以实现一层for循环解决问题

滑动窗口此题重点变量 j 的含义： j 表示数组的终点索引

（1.） j 初始化为0，这样会实现坐标从左至右移动，同时，sum 也在累加，当sum大于等于target时，（2.）隐含的开端索引i 开始移动，直到不满足sum >= target 得到的就是末端索引为j时最短满足条件的数组。

（2.）为什么j 不能表示起始索引，因为如果为起始索引，那么函数实现的原理就会和暴力解法的双层for一致了，没有意义。

Leetcode59: 螺旋矩阵

题目分析：属于模拟过程题

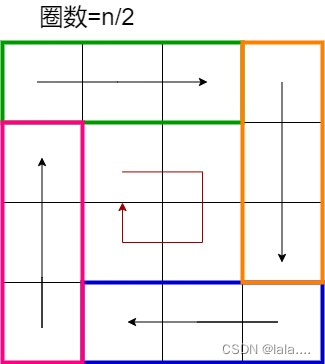
Java实现代码：

class Solution {
    public int[][] generateMatrix(int n) {
        int[][] matrix = new int[n][n];
        int start = 0;
        int count = 1;
        int offset = 1;
        int j,i;
        while((n/2)>=offset){
            for(j = start;j<n-offset;j++){
                matrix[start][j] = count++;        
            }
            for(i = start ;i<n-offset;i++){
                matrix[i][j] = count++;    
            }
            for( ;j>=offset;j--){
                matrix[i][j] = count++;                
            }
            for(;i>=offset;i--){
                matrix[i][j] = count++;       
            }
            offset++;
            start++;
        }
        if(n%2==1){
            matrix[start][start] = count;
        }
        return matrix;

    }
}

细节点：奇偶不同；遍历的时候注意边界点的处理（如四个角），以免重复遍历产生覆盖；

数组部分总结：常用方法有以下四种，主要还是要看数组特点及具体问题进行选择；