2024年最新优化算法——海市蜃楼算法，MATLAB代码免费获取

原创已于 2025-01-07 14:37:01 修改 · 1.5k 阅读

37 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #matlab #python #开发语言

于 2024-11-22 08:02:18 首次发布

注：该算法已按照智能优化算法APP标准格式进行整改，可直接集成到APP中，方便大家与自己的算法进行对比。

海市蜃楼算法（fata morgana algorithm）是一种求解连续多类型优化问题的群智能算法。通过模拟海市蜃楼的形成过程，FATA分别设计了的光滤波原理（MLF）和光传播策略（LPS）。MLF策略结合确定性积分原则，驱动算法种群提高FATA的探索能力。LPS策略结合三角原理，驱动算法个体，提高算法的收敛速度和开发能力。

该成果于2024年发表在计算机科学领域2区SCI期刊“Neurocomputing”上，目前被引5次。

1.原理详解

（1）海市蜃楼滤光原理

在fata morgana算法中形成海市蜃楼的多个光被用作总体，而光（x）被用作个体。mirage (xbest)被用作优化目标。在第一阶段，根据基于定积分原理的海市蜃楼滤光原理，动态评估多重光布居。下图左下角的船体发出的多重光线，包括经过物理变换后形成mirage (xbest)，以及经过物理变换后射向别处而未形成mirage (xbest)。

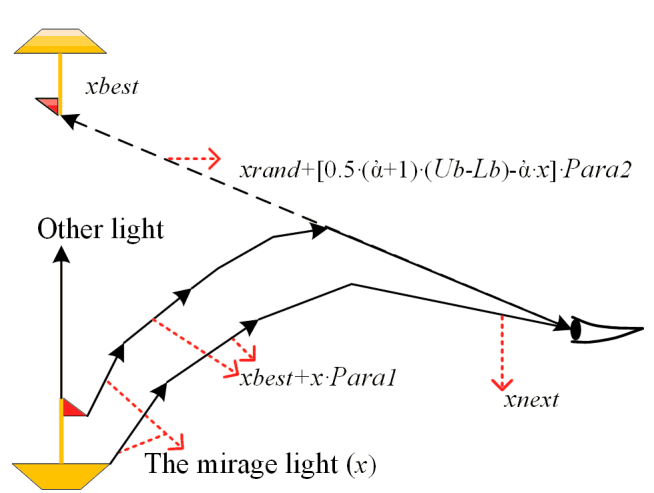
在第二阶段，海市蜃楼光种群执行光传播策略。光在密度不均匀介质中传播的物理变化是个体信息交换的过程，算法搜索目标产生海市蜃楼（最优解）。

该部分展示了基于定积分原理的Fata Morgana算法的种群搜索策略。在上图中，在海市蜃楼形成的物理过程中，船体发出两种类型的光线。大多数光线属于第一种类型，它不会传播并形成海市蜃楼。另一种类型的光线会经历物理变换，从而形成海市蜃楼，被称为mirage light (x)。

在FATA中，区分这两种类型的光群对于算法找到是xbest至关重要的。为此，FATA采用基于定积分原理的光群体质量评价策略，对不同类型的光群体进行评价。在群体智能算法中，通过计算个体的适应度，然后对整个群体的适应度值进行聚合来评估群体质量。如图所示，如果对光群体中个体的适应度进行排序，则形成一条累积曲线。为了有效地计算不同类型的灯光群体的适应度，FATA使用定积分来评估下图中的曲线，使用积分值作为适应度的度量。基于定积分原理选择的海市蜃楼光light (x)也被称为过滤后的海市蜃楼光群。

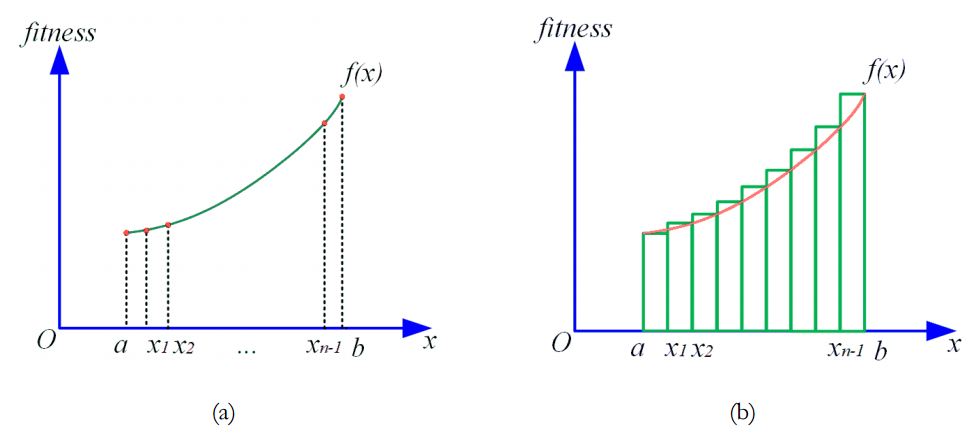
首先，该策略基于种群质量来确定种群为其他光或海市蜃楼光，以执行不同的搜索方法。种群素质是指种群的整体素质。在该策略中，种群适应度函数(f(x))的积分面积（S）代表种群质量。图a示出了群体适应度函数曲线，图b显示了曲线的积分面积（S）。

在SIA中的体能代表着个体的素质。然而，离散的高维适应度值很难作为种群整体素质的评价标准。因此，种群中所有个体的适应度都拟合到一个函数(f(x))。其中，fata morgana算法是基于定积分原理，计算种群适应度函数曲线的积分面积（S）。

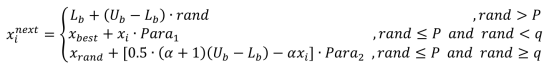
x是光的个体。xnext是新的个体。算法1演示了fata morgana算法的幻影光过滤原理。其中，上述方程分别是前半折射策略、后半折射策略和全内反射策略。P是光总体的品质因数。S的值越小，种群的质量就越好。Sbest代表最佳种群的质量。Sworst代表最差种群的质量。q为单个品质因数。fiti代表当前个体的适应度(x)。

其中Xi表示ith候选解，lb和ub分别表示搜索空间的下界和上界。此外，rand被定义为随机数生成器。Rand(0,1,[1，D])生成一个由D列组成的向量，其中包含均匀分布在[0,1]范围内的随机数。此外，二进制操作表示解决方案的数量，通常比作总体大小。

上述等式给出了基于定积分原理的种群适应度曲线f(x)$(f(x_1) <f(x_n))$的面积计算方法。定积分原理利用极限的概念来计算f(x)的积分面积（s）。>< p> </f(x_n))$的面积计算方法。定积分原理利用极限的概念来计算f(x)的积分面积（s）。><>

（2）光传播原理

FATA中的光传播原理是在海市蜃楼光滤波原理之后执行的，它作为算法的个体搜索策略，负责在搜索空间中进行局部开发以找到局部极小值。如图所示，FATA的光种群，由海市蜃楼光线表示，从左下角的小船开始。首先，它经历了海市蜃楼光过滤策略，其中光群体基于微积分原理进行评估和过滤，以选择形成海市蜃楼现象的个体。此外，过滤后的海市蜃楼光群依次经历折射和反射。在图中可以观察到折射和反射期间光群体的个体变化。光线在图中所示的折射和反射过程中会改变方向和大小。作为个体搜索策略，在搜索空间中执行局部挖掘以找到局部最小值。

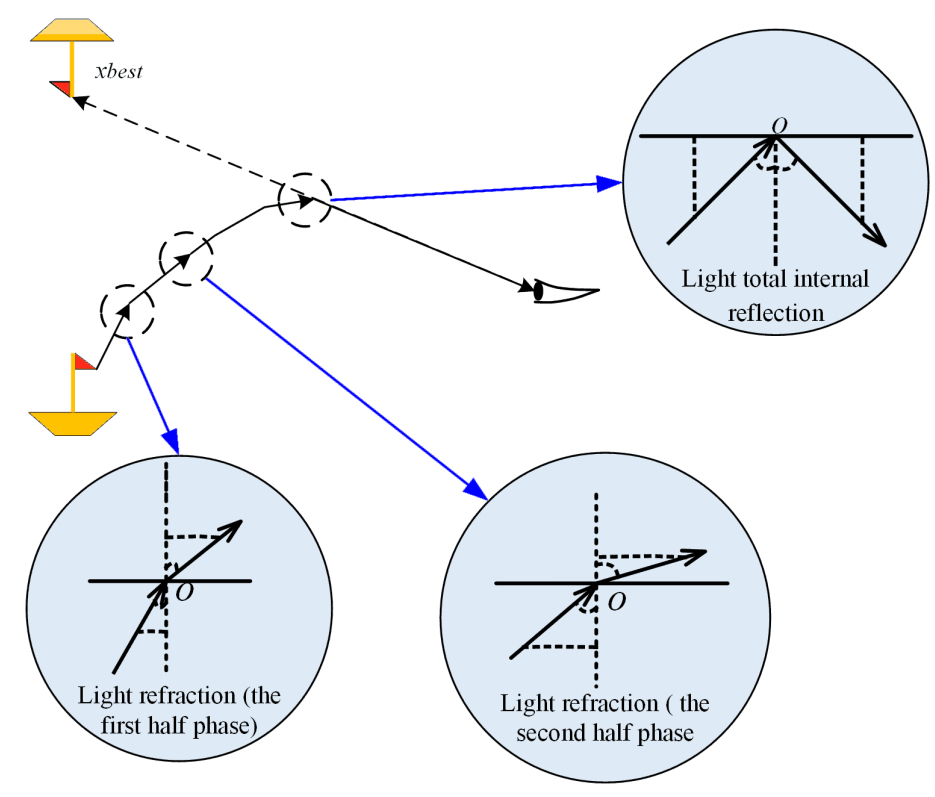
fata morgana算法基于光传播原理结合三角函数设计了个体搜索策略。算法选择执行反射策略(前半阶段)、反射策略(后半阶段)和基于个体质量因子的折射策略。

光的折射(前半阶段)。在下图中，光在前半折射中进入密度不均匀的介质，从光密度较大的介质向光密度较薄的介质传播，改变了光的方向和大小。入射角(i1)小于折射角(i2)。

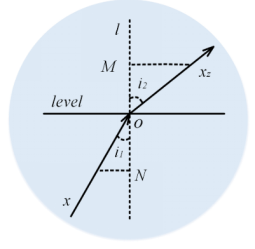
下图分析了光个体的折射过程。光的个体是x。level是折射面的表面。在方程中，xnext是经过上半场反思策略后的新个体。假设，其中的变量为常数。以下是策略的对应公式：

xnext是新的个体。xbet是目前最好的个体。Xz表示策略的折射步骤。Para1是前半阶段的折射率。Para1在光的传播过程中正在发生变化。在公式中，为了简单地测量折射过程中的入射角(i1)和反射角(i2)，参数θ代替了fata morgana算法中的角度变化，θ∈[0，1]。

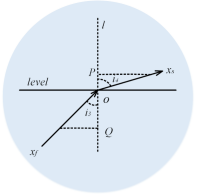
光线折射（后半阶段）。在执行前半折射阶段之后，光在随机点处执行后半折射阶段。下图分析了光的后半折射过程。入射角i3小于折射角i4。光在密度不均匀的介质中传播，因此折射率（para2）连续变化。在后半折射策略中，光个体（xf）将基于搜索空间中的随机个体（xnest）生成新个体（xrand）。以下公式是FATA策略的公式。

XS是后半这段折射策略中的折射步骤。Xrand是种群中的一个随机个体。Para2是第二个反射率。在下图a中，Para1的值在[-2，2]之间随机振荡，并随着迭代次数的增加逐渐接近零。

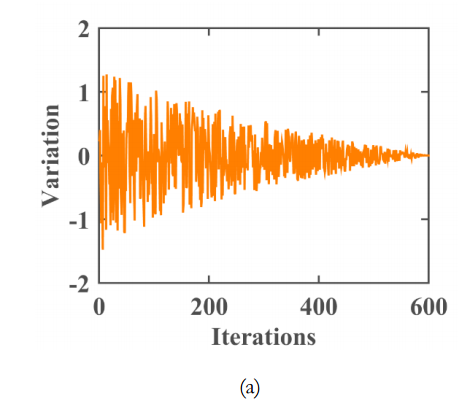
在图b中，Para2的值在[-150，150]之间随机振荡，并随着迭代次数逐渐增加。在图中发现，这两个参数的值相对较大。为了使标准化，将标准化的Para1和Para2进行了标准化。该策略将两个参数缩放到区间[0，1]。在fata morgana算法的最后阶段的显著振荡增强了避免局部最优的能力。

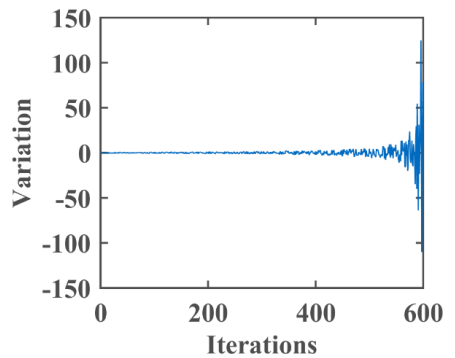
光全内反射。全内反射阶段是海市蜃楼现象形成过程中光传播的最后阶段。这是因为随着折射角的增大，光在密度不均匀的介质中发生全内反射。全内反射策略驱使FATA人群向相反的方向探索。下图分析了光的反射过程。入射角i5等于反射角i6。在图中，O(x0,0)是区间([Lb，Ub])的中心点。其中，E和F的距离分别为入射光和折射光到水平面的距离；在策略中，将光个体(x)转化为个体(xnext)，以寻找相反方向的目标。以下公式为fata morgana算法的策略：

xf是被整个内部反射策略所反映的个体。α是反射策略的反射率。α控制着光个体的变化模式。当α大于1时，xnext穿过边界，α属于[0,1]。Ub代表个体范围的上限，Lb代表个体范围的下限。

FATA算法的流程图如下所示。

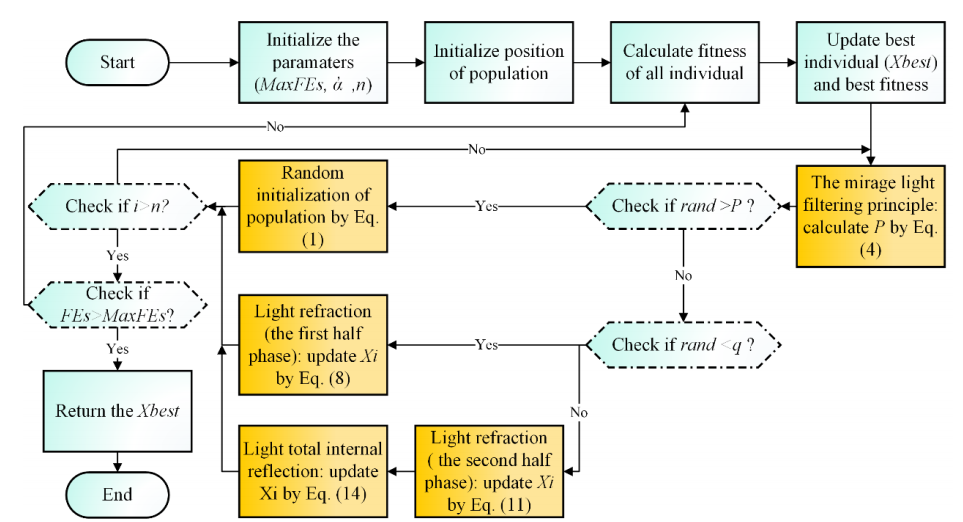
2.结果展示

老规矩，采用作者独创的智能优化算法APP轻松对比一下本期算法。

在CEC2017函数上与其他算法对比一下试试：

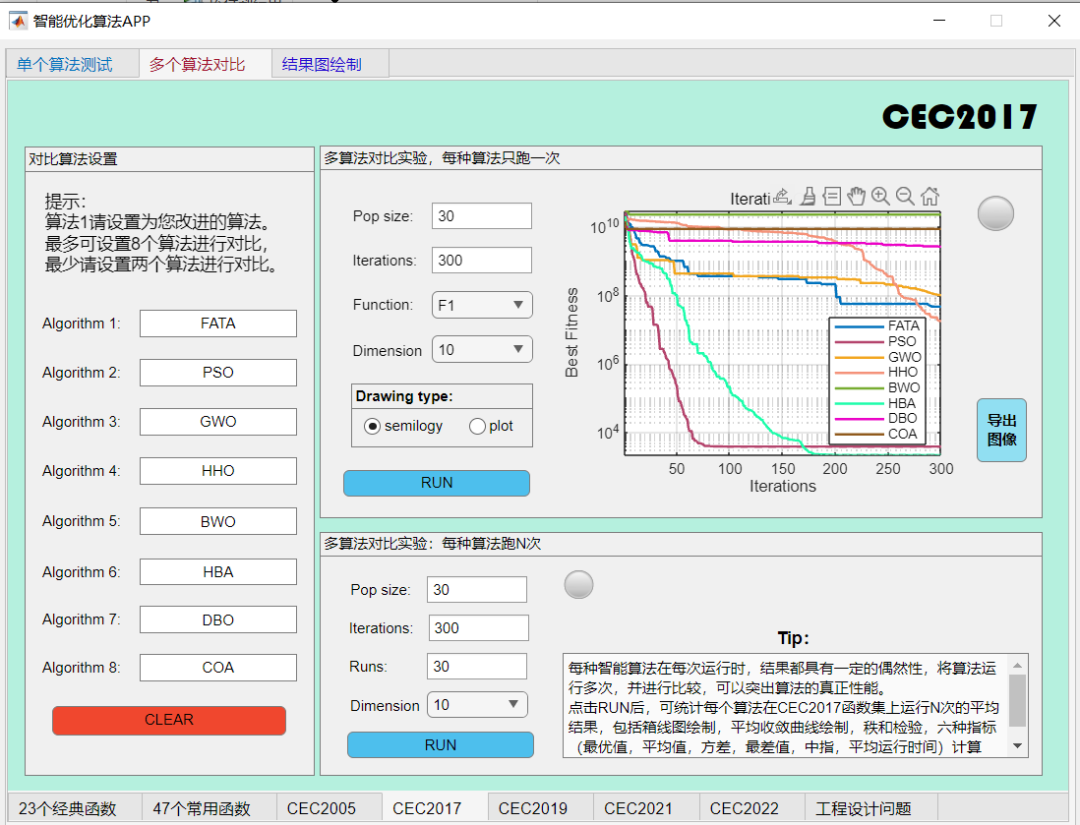
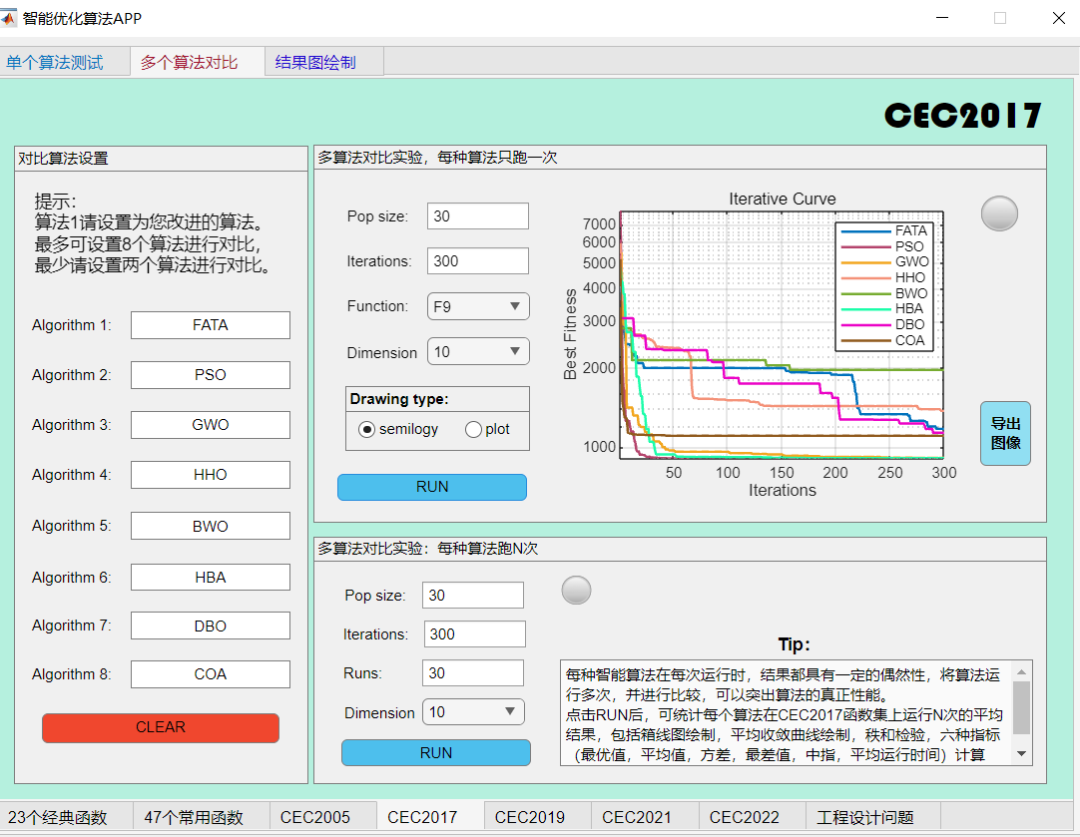
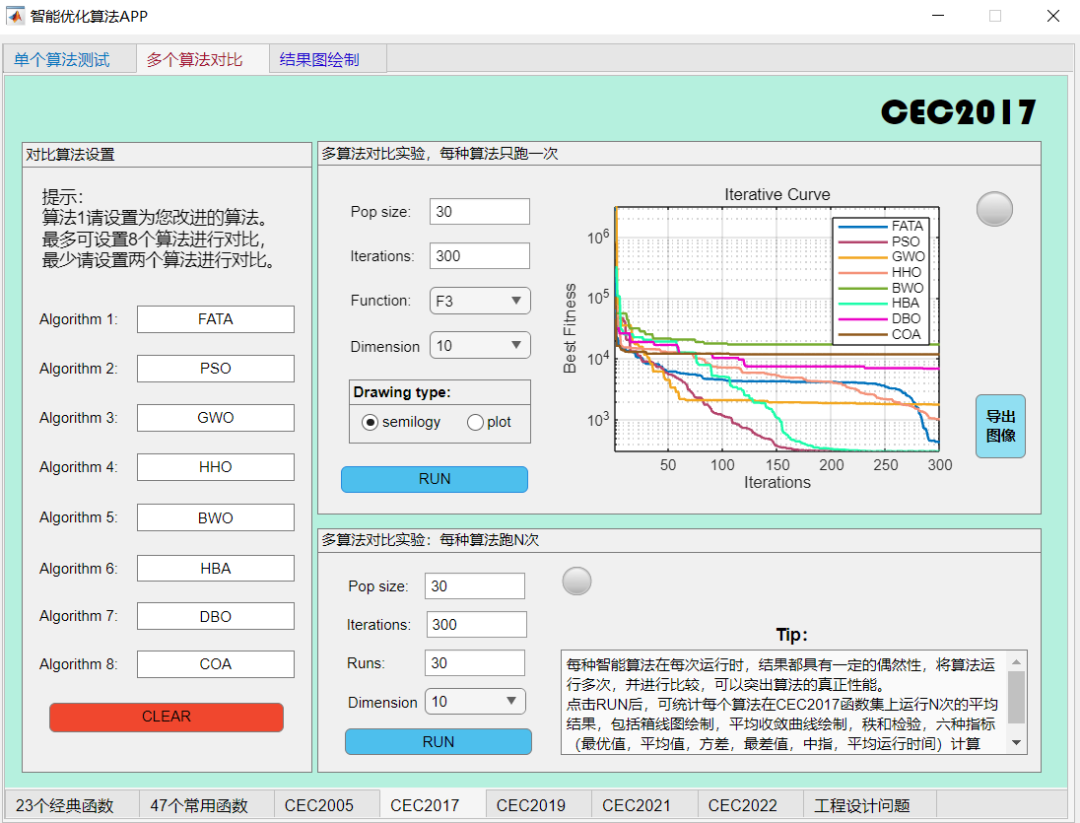
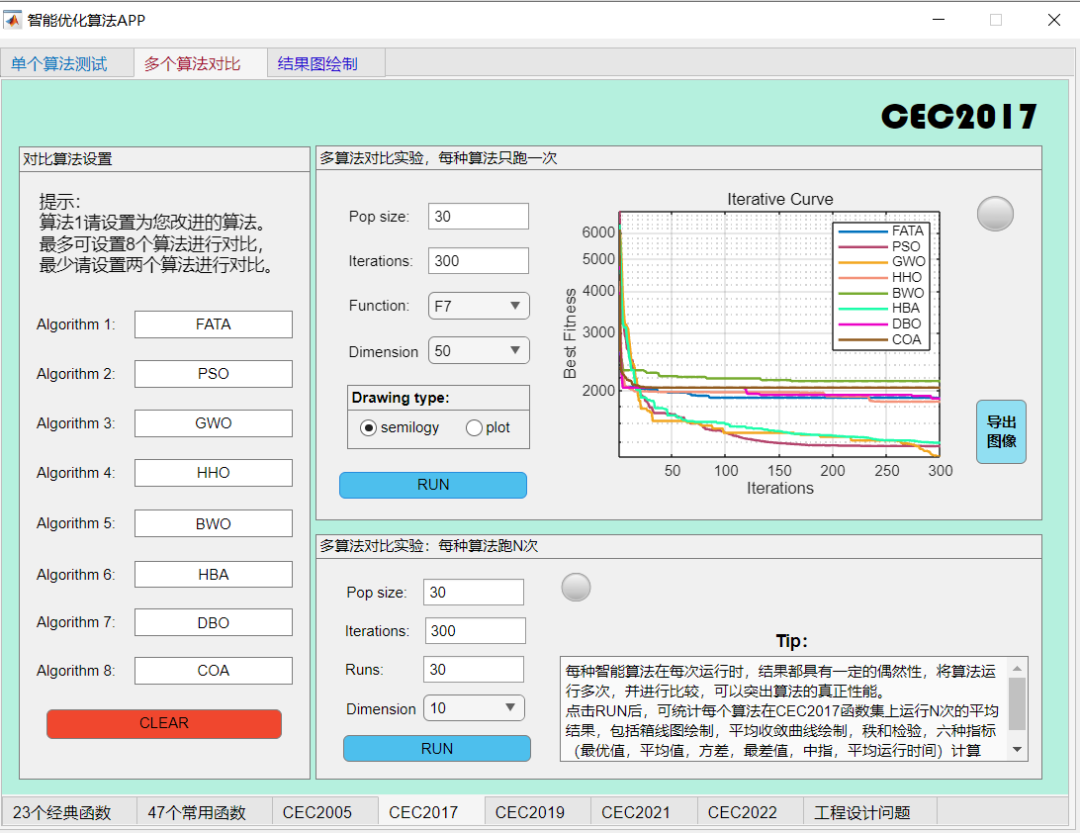
评价：算法性能处于中等。不算很弱，但也不是最强。

3.MATLAB核心代码

%微信公众号搜索：淘个代码，获取更多免费代码
function [gBestScore,bestPos,cg_curve]=FATA(N,MAXITER,lb,ub,dim,fobj)
% initialize position
 worstInte=0; %Parameters of Eq.(4)
 bestInte=Inf;%Parameters of Eq.(4)
noP=N;
arf=0.2;%Eq. (15) reflectance=0.2
gBest=zeros(1,dim);
cg_curve=[];
gBestScore=inf;%change this to -inf for maximization problems
Flight=initialization(noP,dim,ub,lb);%Initialize the set of random solutions
fitness=zeros(noP,1)+inf;
% it=1;%Number of iterations
it=1;    
FEs=0;
lb=ones(1,dim).*lb; % lower boundary 
ub=ones(1,dim).*ub; % upper boundary
% Main
MaxFEs = 10000;
while  it < MAXITER+1
    for i=1:size(Flight,1)     
        Flag4ub=Flight(i,:)>ub;
        Flag4lb=Flight(i,:)<lb;
        Flight(i,:)=(Flight(i,:).*(~(Flag4ub+Flag4lb)))+ub.*Flag4ub+lb.*Flag4lb;
        FEs=FEs+1;    
        fitness(i)=fobj(Flight(i,:));
         %Make greedy selections
        if(gBestScore>fitness(i))
            gBestScore=fitness(i);
            gBest=Flight(i,:);
        end
    end
    [Order,Index] = sort(fitness);  
    worstFitness = Order(N); 
    bestFitness = Order(1);
 %% The mirage light filtering principle 
 Integral=cumtrapz(Order);
 if Integral(N)>worstInte
     worstInte=Integral(N);
 end
  if Integral(N)<bestInte 
     bestInte =Integral(N);
 end
IP=(Integral(N)-worstInte)/(bestInte-worstInte+eps);% Eq.(4) population quality factor
 %% Calculation Para1 and Para2
    a = tan(-(FEs/MaxFEs)+1);
    b = 1/tan(-(FEs/MaxFEs)+1);
    %% 
     for i=1:size(Flight,1) 
         Para1=a*rand(1,dim)-a*rand(1,dim); %Parameters of Eq.(10)
         Para2=b*rand(1,dim)-b*rand(1,dim);%Parameters of Eq.(13)
         p=((fitness(i)-worstFitness))/(gBestScore-worstFitness+eps);% Parameters of Eq.(5) individual quality factor
         %% Eq.(1) 
         if  rand>IP 
             Flight(i,:) = (ub-lb).*rand+lb;
         else
        for j=1:dim
            num=floor(rand*N+1);
            if rand<p   
            Flight(i,j)=gBest(j)+Flight(i,j).*Para1(j);%Light refraction(first phase)  Eq.(8)      
            else   
            Flight(i,j)=Flight(num,j)+Para2(j).*Flight(i,j);%Light refraction(second phase)   Eq.(11)    
            Flight(i,j)=(0.5*(arf+1).*(lb(j)+ub(j))-arf.*Flight(i,j));%Light total internal reflection Eq.(14)  
            end      
        end
        end
     end     
    cg_curve(it)=gBestScore;
    it=it+1;
    bestPos=gBest;
end
end

4.参考文献

[1Qi A, Zhao D, Heidari A A, et al. FATA: an efficient optimization method based on geophysics[J]. Neurocomputing, 2024, 607: 128289.

下方卡片获取代码