SCI一区算法-菲克定律优化，原理详解，MATLAB代码免费获取

原创已于 2025-01-07 14:57:47 修改 · 544 阅读

CC 4.0 BY-SA版权

文章标签：

于 2024-08-28 09:30:08 首次发布

菲克定律优化(Fick’s Law Algorithm, FLA)是一种新的基于物理的元启发式算法，该优化算法利用了菲克第一扩散规则。根据菲克扩散定律，分子倾向于从浓度高的区域向浓度低的区域扩散。通过一系列的实验来测试FLA的性能和解决不同优化问题的能力。

该成果于2023年发表在计算机领域1区SCI期刊“Knowledge-Based Systems”上。该方法收敛曲线速率好，勘探与开发平衡良好，目前被引115次。

1、算法原理

FLA由三个不同的阶段组成，即扩散阶段、平衡阶段和稳态阶段。FLA被认为是一种有效而强大的算法，因为它可以在这两个阶段之间找到平衡，这意味着探索和利用都是以公平的方式完成的。

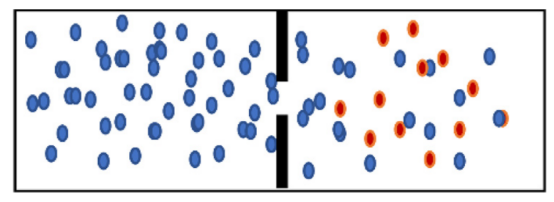
在第一阶段，本研究认为在实验开始时存在两个区域，并且它们之间的浓度差异很大;这导致粒子根据浓度差异从一个区域移动到另一个区域，称之为相位扩散算子(DO);在下图中，本研究考虑两个区域，一个是高浓度区域(区域1)，另一个是低浓度区域(区域2)。根据flick定律，粒子会从区域1移动到区域2。

（1）初始化

在FLA中，优化过程从随机生成一组候选解(X)开始，如下式的矩阵所示，每次迭代的最佳候选解被认为是迄今为止最优解或接近最优解。

其中N为解的个数或总体大小，D为问题维度或决策变量的个数，j为第j个决策变量。

（2）聚类与传递函数

将人口分为两个相等的组N1和N2。

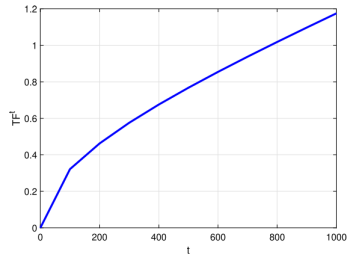
任何优化算法成功的核心都是从探索到开发的转换，而从开发到探索的转换则是从探索到开发的转换。最常用的传递参数是线性参数，在许多问题中，线性参数不能从探索性行为转变为利用性行为。针对这一问题，本文提出了一种非线性传递函数，并将其作为从开采到勘探或从勘探到开采转换的基础。该TF由下式描述，如下图所示。

式中t为迭代次数，t为总迭代次数，C1 = 0.5。

（3）更新分子位置

本研究提出了三个阶段的传输算子，包括DO、EO和SSO。为了在三个阶段之间进行转换，使用以下公式:

（4）扩散算子(DO)(勘探阶段)

一开始，两个区域的浓度差异很大，这导致分子根据给定区域的浓度从一个区域转移到另一个区域。本文提出参数(Tt DO)，可以由下式给出:

根据Tt DO值确定流动方向为:

首先考虑区域i的浓度高于区域j。据此，一些分子从i区移动到j区，i区剩下的分子会受到这个事件的影响。从i区域到j区域的分子数如下:

其中NTij是指从i基团转移到j基团的分子数，C3和C4分别为0.1和0.2的常数。

停留在i的基团上的分子数可由下式求得:

分子NTij将移动到另一个区域，它们的位置将主要在j区域的最佳平衡分子上更新，使用:

式中，Xt EO,j为区域j的平衡位置，DFt i为方向因子，等于{−1,1}，该方向因子随机变化，在给定搜索区域内给予较高的扫描机会，并脱离局部最优，r2为随机数∈[0，1]，DOF是随时间变化的流动方向，可由下式给出:

继续存在于区域i中的i组（NRi）中的分子根据不同的三个阶段之间的导航来更新它们的位置：（1）区域i中的平衡位置，（2）区域i中的平衡位置和问题的边界，或（3）它们的位置没有变化。下面的等式用于模拟该策略：

式中Xt EO,i为区域i中的平衡位置，U&L为问题的上下边界，r3为区间[0,1]内的随机数。

对于j的分子，由于j区域的浓度更高，它们在同一区域内改变位置而不移动，因此它们根据j区域的平衡位置更新自己的位置，所用问题的边界可由下式计算:

如果区域i浓度较低，如果区域j浓度较高，则会考虑上述策略，反之则会发生，即分子从j区域移动到i区域。

（5）平衡算子(EO)(从勘探到开采的过渡阶段)

这一阶段被认为是从勘探到开发的过渡阶段。分子通过以下方式更新它们的位置:

其中，Xt p,g是粒子p在组g中的位置，Xt EO,g是组g中的平衡位置。

其中，Qt EO,g是指g组中区域的相对量。

（6）稳态算子（SSO）（开发阶段）

优化搜索的最后阶段是开发或稳定阶段，分子使用以下公式更新其位置：

其中Xt SS是稳态位置，Xt p,g是粒子p的位置。

是指区域G和运动步长的相对量。它们可以使用下式计算。

其中，DFt g是等于± 1的方向因子，Rt 1是区间[0，1]中的随机数，DRFt g是指扩散速率因子。

FLA对应的伪代码过程如下图所示

2、结果展示

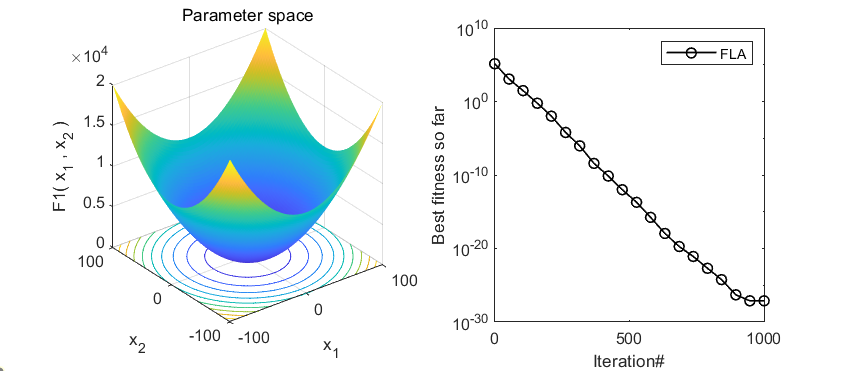
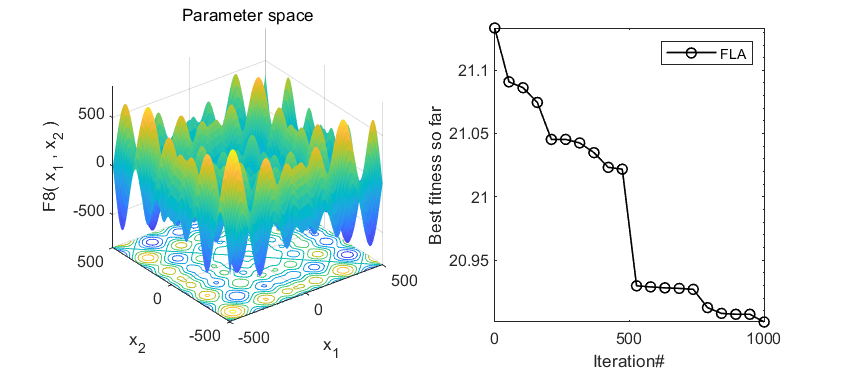
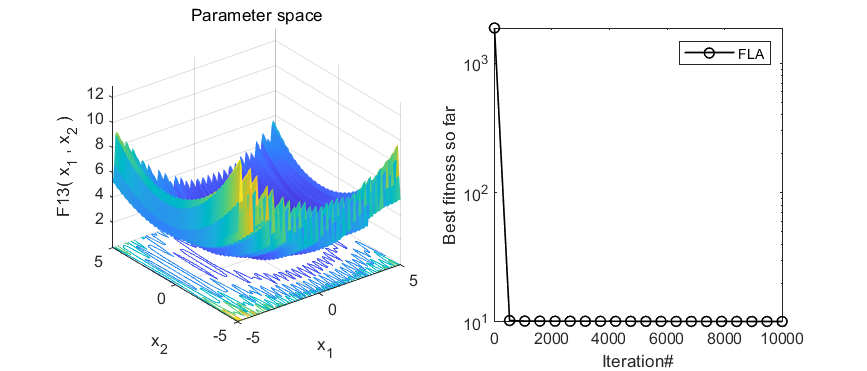
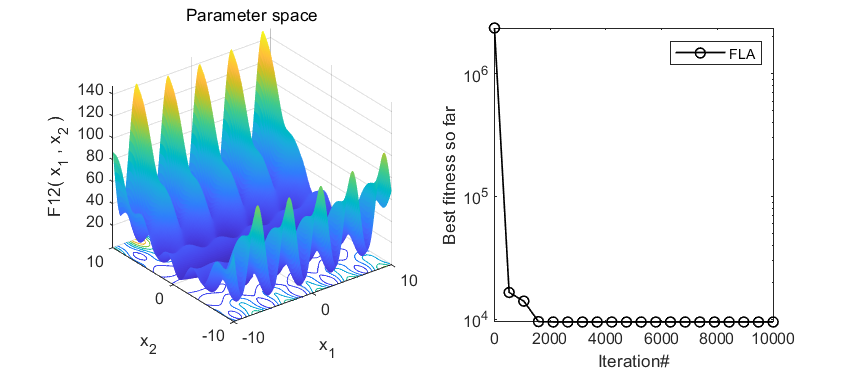
3、MATLAB核心代码


% 菲克定律优化(Fick’s Law Algorithm, FLA)
function [Xss, BestF, CNVG] = FLA( NoMolecules, T,lb,ub, dim,objfunc)
C1=0.5;C2=2;c3=.1;c4=.2;c5=2;
D=.01;
X=lb+rand(NoMolecules,dim)*(ub-lb);%intial postions
for i=1:NoMolecules
FS(i) = feval(objfunc,X(i,:));
end
[BestF, IndexBestF] = min(FS);
Xss = X(IndexBestF,:);
n1=round(NoMolecules/2);
n2=NoMolecules-n1;
X1=X(1:n1,:);
X2=X(n1+1:NoMolecules,:);
for i=1:n1
FS1(i) = feval(objfunc,X1(i,:));
end
for i=1:n2
FS2(i) = feval(objfunc,X2(i,:));
end
[FSeo1, IndexFSeo1] = min(FS1);
[FSeo2, IndexFSeo2] = min(FS2);
Xeo1 = X1(IndexFSeo1,:);
Xeo2 = X2(IndexFSeo2,:);
vec_flag=[1,-1];
  if FSeo1<FSeo2
        FSss=FSeo1;
        YSol=Xeo1;
    else
        FSss=FSeo2;
        YSol=Xeo2;
    end
for t = 1:T
    TF(t)=sinh(t/T)^C1;
    X=[X1;X2];
    %             DO
    if TF(t)<0.9
           DOF=exp(-(C2*TF(t)-rand))^C2;
            TDO=c5*TF(t)-rand;%   direction of flow
            if (TDO)<rand
                %         select no of molecules
                M1N = c3*n1;
                M2N = c4*n1;
                NT12 =round((M2N-M1N).*rand(1,1) + M1N);
                for u=1:NT12
                    flag_index = floor(2*rand()+1);
                    DFg=vec_flag(flag_index);
                    Xm2=mean(X2);
                    Xm1=mean(X1);
                    J=-D*(Xm2-Xm1)/norm(Xeo2- X1(u,:)+eps);
                    X1new(u,:)= Xeo2+ DFg*DOF.*rand(1,dim).*(J.*Xeo2-X1(u,:));
                end
                for u=NT12+1:n1
                    for tt=1:dim
                        p=rand;
                        if p<0.8
                            X1new(u,tt) = Xeo1(tt);
                        elseif p<.9
                            r3=rand;
                            X1new(u,tt)=X1(u,tt)+DOF.*((ub-lb)*r3+lb);
                        else
                            X1new(u,tt) =X1(u,tt);
                        end
                    end
                end
                for u=1:n2
                    r4=rand;
                    X2new(u,:)= Xeo2+DOF.*((ub-lb)*r4+lb);
                end
            else
                M1N = .1*n2;
                M2N = .2*n2;
                Ntransfer =round((M2N-M1N).*rand(1,1) + M1N);
                for u=1:Ntransfer
                    flag_index = floor(2*rand()+1);
                    DFg=vec_flag(flag_index);
                    R1=randi(n1);
                    Xm1=mean(X1);
                    Xm2=mean(X2);
                    J=-D*(Xm1-Xm2)/norm(Xeo1- X2(u,:)+eps);
                    X2new(u,:)=  Xeo1+DFg*DOF.*rand(1,dim).*(J.*Xeo1-1*X2(u,:));
                end
                for u=Ntransfer+1:n2
                    for tt=1:dim
                        p=rand;
                        if p<0.8
                            X2new(u,tt) = Xeo2(tt);
                        elseif p<.9
                            r3=rand;
                            X2new(u,tt)=X2(u,tt)+DOF.*((ub-lb)*r3+lb);
                        else
                            X2new(u,tt) =X2(u,tt);
                        end
                        
                    end
                end
                for u=1:n1
                    r4=rand;
                    X1new(u,:)= Xeo1+DOF.*((ub-lb)*r4+lb);
                end
            end
    else
%         Equilibrium operator (EO)
        if TF(t)<=1
            for u=1:n1
                flag_index = floor(2*rand()+1);
                DFg=vec_flag(flag_index);
                Xm1=mean(X1);
                Xmeo1=Xeo1;
                J=-D*(Xmeo1-Xm1)/norm(Xeo1- X1(u,:)+eps);
                DRF= exp(-J/TF(t));
                MS=exp(-FSeo1/(FS1(u)+eps));
                R1=rand(1,dim);
                Qeo=DFg*DRF.*R1;
                X1new(u,:)= Xeo1+Qeo.*X1(u,:)+Qeo.*(MS*Xeo1-X1(u,:));
            end
            for u=1:n2
                flag_index = floor(2*rand()+1);
                DFg=vec_flag(flag_index);
                Xm2=mean(X2);
                Xmeo2=Xeo2;
                J=-D*(Xmeo2-Xm2)/norm(Xeo2- X2(u,:)+eps);
                DRF= exp(-J/TF(t));
                MS=exp(-FSeo2/(FS2(u)+eps));
                R1=rand(1,dim);
                Qeo=DFg*DRF.*R1;
                X2new(u,:)=  Xeo2+Qeo.*X2(u,:)+Qeo.*(MS*Xeo1-X2(u,:));
            end
        else
            %     Steady state operator (SSO):
                for u=1:n1
            flag_index = floor(2*rand()+1);
            DFg=vec_flag(flag_index);
            Xm1=mean(X1);
            Xm=mean(X);
            J=-D*(Xm-Xm1)/norm(Xss- X1(u,:)+eps);
            DRF= exp(-J/TF(t));
            MS=exp(-FSss/(FS1(u)+eps));
            R1=rand(1,dim);
            Qg=DFg*DRF.*R1;
            X1new(u,:)=  Xss+Qg.*X1(u,:)+Qg.*(MS*Xss-X1(u,:));
        end
        for u=1:n2
            Xm1=mean(X1);
            Xm=mean(X);
            J=-D*(Xm1-Xm)/norm(Xss- X2(u,:)+eps);
            DRF= exp(-J/TF(t));
            MS=exp(-FSss/(FS2(u)+eps));
            flag_index = floor(2*rand()+1);
            DFg=vec_flag(flag_index);
                        Qg=DFg*DRF.*R1;
            X2new(u,:)= Xss+ Qg.*X2(u,:)+Qg.*(MS*Xss-X2(u,:));
        end
        end
    end
    for j=1:n1
FU=X1new(j,:)>ub;FL=X1new(j,:)<lb;X1new(j,:)=(X1new(j,:).*(~(FU+FL)))+ub.*FU+lb.*FL;
        v = feval(objfunc,X1new(j,:));
        if v<FS1(j)
            FS1(j)=v;
            X1(j,:)= X1new(j,:);
        end
    end
    for j=1:n2
FU=X2new(j,:)>ub;FL=X2new(j,:)<lb;X2new(j,:)=(X2new(j,:).*(~(FU+FL)))+ub.*FU+lb.*FL;
        v = feval(objfunc,X2new(j,:));
        if v<FS2(j)
            FS2(j)=v;
            X2(j,:)= X2new(j,:);
        end
    end
    [FSeo1, IndexFSeo1] = min(FS1);
    [FSeo2, IndexFSeo2] = min(FS2);
    
    Xeo1 = X1(IndexFSeo1,:);
    Xeo2 = X2(IndexFSeo2,:);
    if FSeo1<FSeo2
        FSss=FSeo1;
        YSol=Xeo1;
    else
        FSss=FSeo2;
        YSol=Xeo2;
    end
    CNVG(t)=FSss;
    if FSss<BestF
        BestF=FSss;
        Xss =YSol;
    end
end
end

参考文献

[1]Hashim F A, Mostafa R R, Hussien A G, et al. Fick’s Law Algorithm: A physical law-based algorithm for numerical optimization[J]. Knowledge-Based Systems, 2023, 260: 110146.

完整代码获取

点击下方卡片获取。

后台回复关键词：

TGDM815